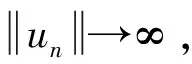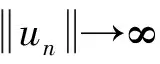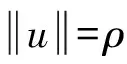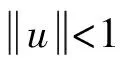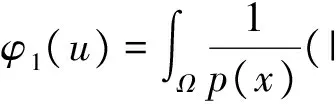一类含Hardy奇异项的p(x)-Laplace方程的正解
2011-01-19邓志颖刘祥清
邓志颖,刘祥清
(1.重庆邮电大学 应用数学研究所,重庆 400065;2.云南师范大学 数学学院,云南 昆明 650092;3.苏州大学 数学科学学院,江苏 苏州 215006)
1 引言与主要结果
本文讨论一类含Hardy奇异项的p(x)-Laplace方程:
(1)
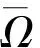
形如方程(1)这类带Hardy奇异项的变指数椭圆方程有着广阔的物理背景和几何背景,在导电材料的热传导理论、异质化学催化剂理论和奇异极小曲面等诸多实际问题中都有应用[1].当μ=0时,方程(1)非奇异,这类非奇异的变指数椭圆方程可以参见文献[2-6]与其中所含的文献等.当μ≠0时,此时方程具有奇异项.文献[7]研究了下述奇异p(x)-Laplace方程:
(2)
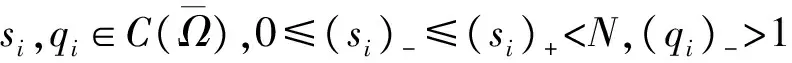
(3)
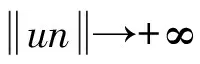
其中Ω=Ω′×RN-k,Ω′是Rk(1 讨论方程(1)的一个出发点是下述有关变指数空间的基本理论与相关引理.设S(Ω)是Ω上全体(实)可测函数构成的集合.记: W1,p(x)(Ω)={u∈Lp(x)(Ω):|▽u|∈Lp(x)(Ω)}, 在Lp(x)(Ω)上赋以Luxemburg范数: 引理1[2-3]设1 (i)(Poincáre不等式)存在C=C(Ω)>0,使得: (ii)(Hölder不等式)∀u∈Lp(x)(Ω),v∈Lp′(x)(Ω),有: 现在进一步考察具有权函数的变指数Lebesgue空间.设a∈S(Ω),且∀x∈Ω,a(x)>0,记: (i)对u≠0,λ>0,|u|(p(x),a(x))=λ⟺ρa(x)(u/λ)=1; (ii)|u|(p(x),a(x))<1(=1;>1)⟺ρa(x)(u)<1(=1;>1); (vi)|uk|(p(x),a(x))→∞(k→∞)⟺ρa(x)(uk)→∞(k→∞). 讨论方程(1)的另一个重要依据是变指数空间中的下述Hardy不等式. 引理4(Hardy不等式[4]) 设Ω是RN中的一个有界开集,δ=dist(x,∂Ω),Ωc=RNΩ满足条件: (H) ∃l>0,s.t. |Br(z)∩Ωc|≥l|Br(z)|,∀z∈∂Ω,r>0. 其中Br(z)是RN中以z为心半径为r的球,|·|表示其测度.并设p(x):Ω|→[1,∞)在Ω上具有log-Hölder连续性,即: 则存在只依赖于p,N和l的常数C>0,a0>0,使得: 特别地,取a=0时,有: (4) 由上述Hardy不等式(4),从而可以定义: (5) 结合引理3与引理4可以建立本文的一个重要引理. 引理5 在引理4的条件下,下述结论成立: (6) (7) 又由引理3可知: (8) (9) (10) 下面分成四种情形分别进行讨论. (11) 其中f(x,u)是满足适当条件的Caratheodory函数.为简单起见,只讨论f(x,u)的两种具体情形. 情形(I):f(x,u)=a(x)|u|q(x)-2u,即讨论方程: 主要结果可以概括为: 1)当μ≤0,q+ 情形(II)f(x,u)=σ|u|r(x)-2u+b(x)|u|q(x)-2u,即讨论方程: 主要结果是: (12) 容易验证I∈C1(X,R),从而泛函I的临界点即为方程(P)的(弱)解.为证得定理1,首先给出下述引理. 引理6[1]p(x)-Laplace算子Δp(x):X→X*是严格单调的同胚映射. 引理7 当μ≤0,q+ 定理1的证明分两种情形来进行讨论. (13) 其中u+=max{u(x),0}.容易验证J∈C1(X,R),且∀u,v∈X,有: (14) 下面分三步来证明定理1中的结论. (15) 另一方面,当n→∞时,有: ▽un|p(x)-2▽un-|▽u|p(x)-2▽u)▽νdx- 结合上式与式(15)可知: ▽un|p-2▽un-|▽u|p-2▽u)▽νdx→0,∀ν∈X. 在上式中取ν=un-u,并结合引理6立即可知:un→u于X. 可知:当t>1充分大时,有J(tu)<0. 3° 证明方程(P)非负非平凡解的存在性.结合1°,2°与山路引理[8]得出J具有非平凡临界点u,即∀ν∈X,有 从而u-≡0,u=u+≥0,又由2°可知J(u)≥α>0=J(0),从而u≢0,故u是方程(P)的非负非平凡解.特别地,当μ≤0时,由p(x)-Laplace方程的强极大值原理[10]可知u是方程(P)的正解. 本节的主要讨论方程(Q),并证明定理2.考察X上的能量泛函: (16) 其中u+=max{u(x),0},易知φ∈C1(X,R),且∀u,ν∈X,有: (17) 为证明定理2,首先给出下述引理. 引理8 若u是φ的临界点,则u是方程(Q)的非负解. 证明设u是X的临界点,从而∀ν∈X,有<φ′(u),ν>=0,取ν=u-=min{u(x),0}.结合式(6)与式(17)可知u-≡0,从而u=u+≥0,即u为方程(Q)的非负解. 引理9φ在X上满足(P.S)条件. (18) 注意到q->p+,从而当σ>0充分小时结论成立. 引理11 任给正值函数u∈X,则(i)当t>0充分小时,有φ(tu)<0;(ii)当t→+∞时,有φ(tu)→-∞. 证明设u∈X且在Ω中有u>0,一方面,当t∈(0,1)时,由r+ φ(tu)≤C11tp--C12tr+. 可知i)成立.另一方面,当t>1时,由q->p+与: φ(tu)≤C13tp+-C14tr--C15tq-. 可知ii)成立. 定理2的证明由引理9-11可知泛函φ满足山路引理[8]的全部条件,从而φ有非平凡临界点u1,使得φ(u1)>α>0.由引理8可知u1是方程(Q)的一个非负非平凡解.进一步,若μ≤0,则由强极大值原理[10]可知:u1>0,即u1是方程(Q)的一个正解.另一方面,当μ≤0时,记: φ(u)=φ1(u)-φ2(u)-φ3(u), φ(u1)>α>0>φ(u2). 故u2≠0,u2≠u1.易知u2是球B(0)的内点,从而u2是φ的临界点,这样,由引理8和强极大值原理[11]得出:u1和u2是方程(Q)的两个不同正解.定理2得证. [1] Dupaigne L,Ghergu M,Radulescu V.Lane-emden-Fowler equations with convection and singular potential[J].J Math Pures Appl, 2007,87:563-581. [2] Fan X, Zhao D. On the spacesLp(x)(Ω) andWm,p(x)(Ω)[J].J Math Anal Appl,2001,263:424-446. [3] Fan X,Shen J,Zhao D.Sobolev embedding theorems for spacesWk,p(x)(Ω)[J].J Math Anal Appl,2001,262:749-760. [4] Harjulehto P, Häastö P,Koskenoja M. Hardy’s inequality in variable exponent Sobolev spaces[J].Georgian Math J,2005,12(3):431-442. [5] 范先令.p(x)-Laplace方程的正解的存在性[J].西北民族学院学报:自然科学版,2000,21(1):1-4. [6] 范先令.一类p(x)-Laplace方程的正解[J].甘肃教育学院学报:自然科学版,2001,15(1):1-3. [7] Fan X. Solutions forp(x)-Laplacian Dirichlet Problems with Singular Coefficients[J].J Math Anal Appl,2005,312:464-477. [9] Raghavendra V, Sreenadh K. Nontrivial solutions for perturbations of a Hardy-Sobolev operator on unbounded domains[J].J Math Anal Appl, 2003, 288: 314-325. [8] Willem M. Minimax theorems[M].Birkhäuser Boston,1996:20-32. [10] 范先令,赵元章,张启虎.p(x)-Laplace方程的强极大值原理[J].数学年刊,2003,24(A):495-500.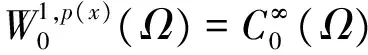


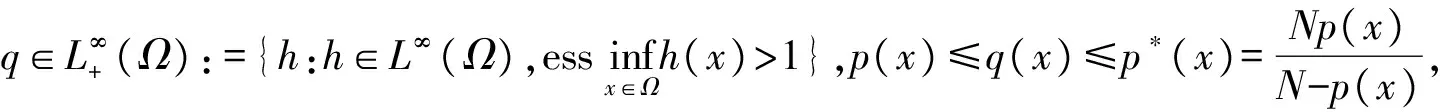


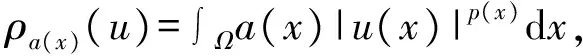
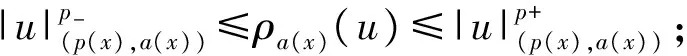
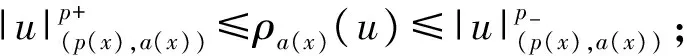
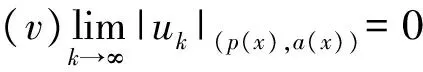
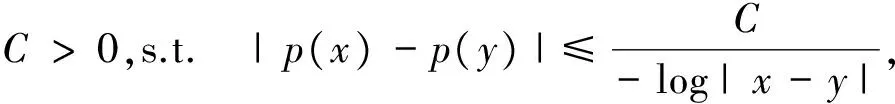

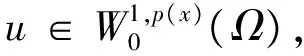
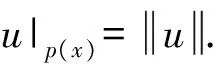
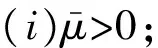
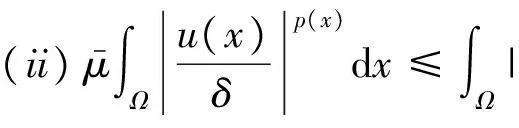

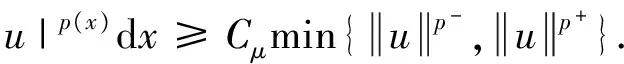


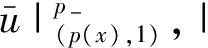

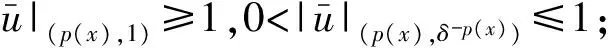
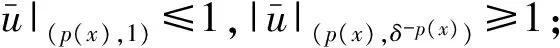
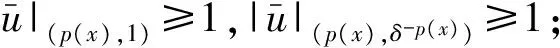
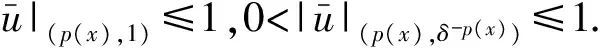
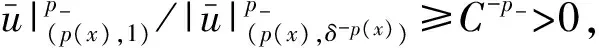
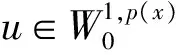
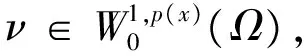
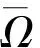
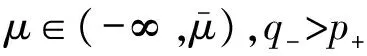
2 方程(P)正解的存在性
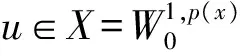
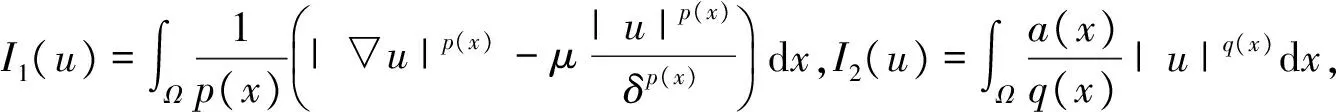
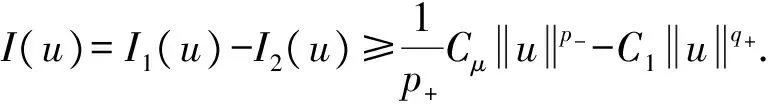
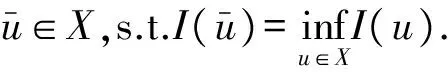
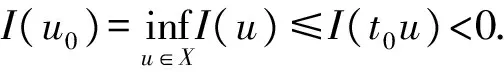
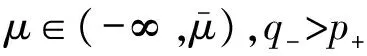

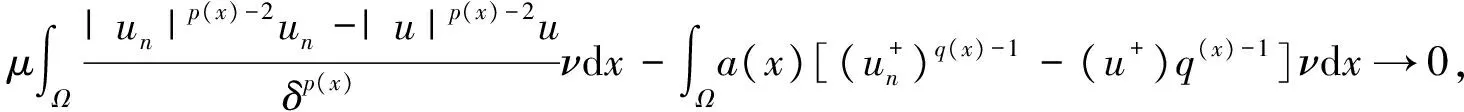
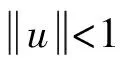
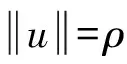
3 方程(Q)多重正解的存在性