运用Matlab软件求普朗克常量

张梦超 潘沈浩 芦立娟

（浙江海洋学院 浙江 舟山 316000）

运用Matlab软件求普朗克常量

张梦超 潘沈浩 芦立娟

（浙江海洋学院 浙江 舟山 316000）

通过Matlab软件对实验数据进行多次拟合，经过对比发现曲线的三次拟合方程的图形比较符合经验图形要求.所以采用三次拟合方程再利用Matlab软件来进行编程计算，阐明了利用拟合方程自动求截止电压的方法，最终求得普朗克常量.

Matlab软件 拟合 曲率法 截止电压 普朗克常量

利用拐点法测得截止电压在求普朗克常量实验中比较常见.通常采用的是在Excel中用散点法取得离散点拟合曲线，然后经比较得出截止电压的点，但因随机性导致取点不准确，这种做法误差相对较大.为了准确获取截止电压，本实验采用Matlab软件拟合出曲线方程，根据数据选取恰当次幂的曲线方程，然后用Matlab软件获得曲线方程在截止电压部分的曲率半径最小值的点，由此得到普朗克常量.这样减小了计算过程中因为拟合不准确和估读数值而带来的误差，从而提高了光电效应测普朗克常量的精度.

1 实验仪器

GD－Ⅲ型光电效应实验仪，电脑等.

2 实验原理

金属在光的照射下释放出电子的现象叫做光电效应.由能量守恒定律有

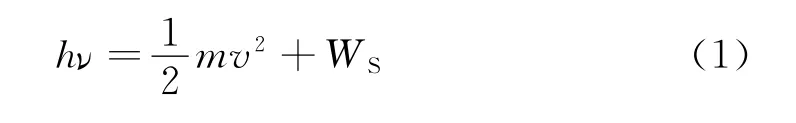
此式称为爱因斯坦光电方程.式中h为普朗克常量，为入射光的频率，m为电子质量，v为电子的最大速度；（1）式右边第一项为电子最大初动能，第二项为金属逸出功.

2.1 根据爱因斯坦光电方程求普朗克常量

本实验采用“减速电位法”确定电子的最大初动能，并由此求出普朗克常量h.实验原理如图1（a）所示.图中K为光电管阴极，A为阳极.当频率为ν的单色光入射到光电管阴极上时，电子从阴极逸出，向阳极运动，形成电流.当UAK＝UA－UK为正值时，UAK越大，光电流IAK越大；当电压UAK达到一定值时，光电流饱和，如图1（b）中虚线所示.若UAK达到某一负值US时，光电流为零，US称为遏止电位或截止电压.这是因为从阴极逸出的具有最大初动能的电子不能穿过反向电场到达阳极，即

式中e为电子电荷.

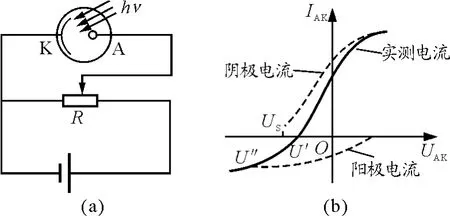
图1

由（1）和（2）式得

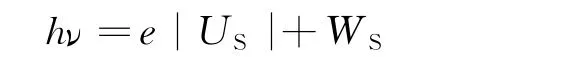
当用不同频率的单色光照射时，有

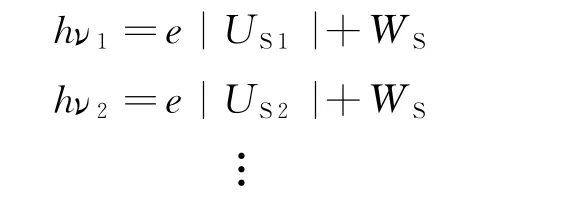
联立其中任意两个方程，可得

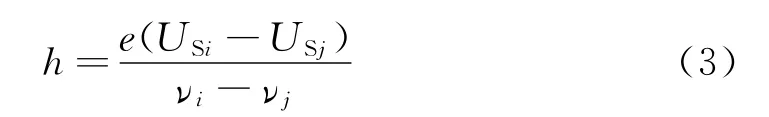
可见，爱因斯坦光电方程提供了一种测量普朗克常量的方法.如果从实验所得的｜US｜－ν关系是一条直线（图2），其斜率，由此可求出常量h.

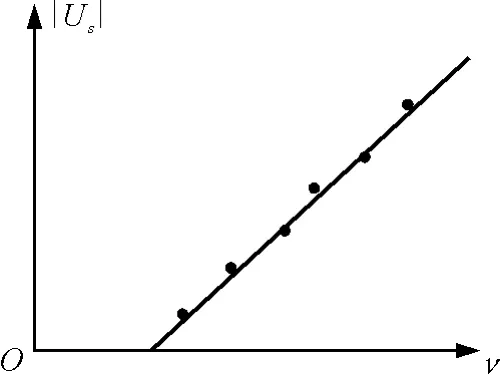
图2

2.2 截止电压的确定

由于光电管的不同，使截止电压US的确定带有很大的任意性.常用于测量US的有“交点法”、“拐点法”.现介绍比较复杂的“曲率法”.利用Matlab软件，具体做法如下.

3 设计方案

3.1 数据测量

安放好光电效应实验仪，用遮光罩罩住光电管暗盒的光窗，打开仪器开关，预热10min以上.调整光电管与汞灯距离L约为30cm保持不变.连接电路，测试前先调零，调零时先将仪器后面板上的电流输入信号开关断开，并将微电流测试仪的“电流调节”换挡开关拨到10－11A挡，电压量程为－3～＋3 V.调节“电流调节”和“电压调节”旋钮，使电流和电压指示分别为零.调好零后再将仪器后面板上的电流信号输入开关接通.除去物镜盖，调节“电压调节”旋钮从－3V或－2V开始，缓慢增加.先粗测一遍，观察不同滤色片下的电流变化情况，记下电流明显变化的电压值.在粗测的基础上，进行精确测量.从短波波长起小心地逐次换上滤色片，仔细读出不同频率入射光照射下的光电流，记录在表1中.在电流开始变化的地方应多读几个数值.

3.2 Matlab软件拟合

3.3 Matlab软件编程 求截止电压

4 实验数据

表1 不同频率下的伏安特性曲线数据

5 数据处理

以波长365nm为例，利用Matlab软件进行方程拟合，共进行多次，编程及运行结果如下.

三次拟合曲线

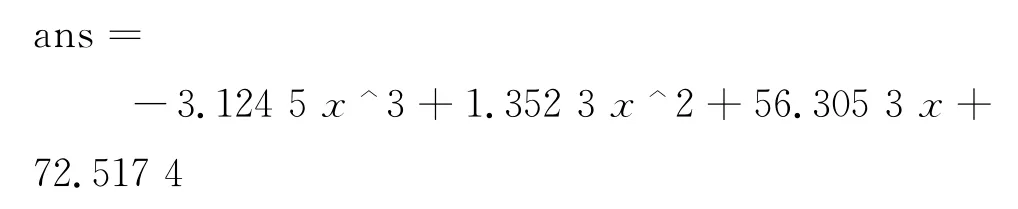
七次拟合曲线

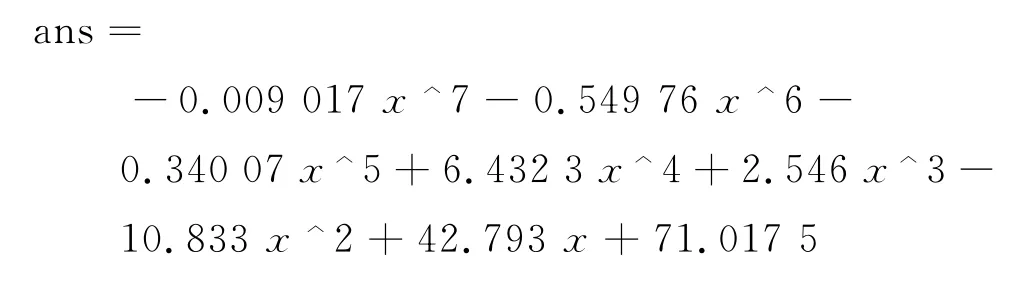
十次拟合曲线

经过对比，发现曲线的三次拟合方程最符合经验公式，所以本文采用三次拟合方程来进行实验计算.又根据截止电压的范围和图形拟合的相似程度来看，本文采用Matlab画出的图形中最有效且包含截止电压的一个大致区间.

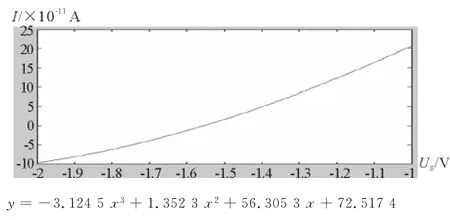
图3

求该曲线上曲率半径最小的点，即要求该曲线的极小值点.根据曲率半径公式 R＝，令其一级导数等于零，整理后得出以下方程

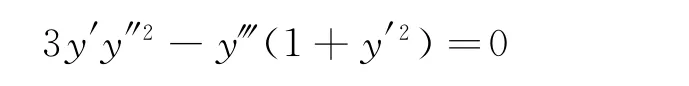
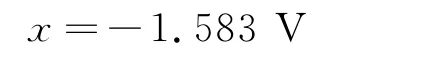
同理，得出其他滤光片波长的截止电压如表2及图4.

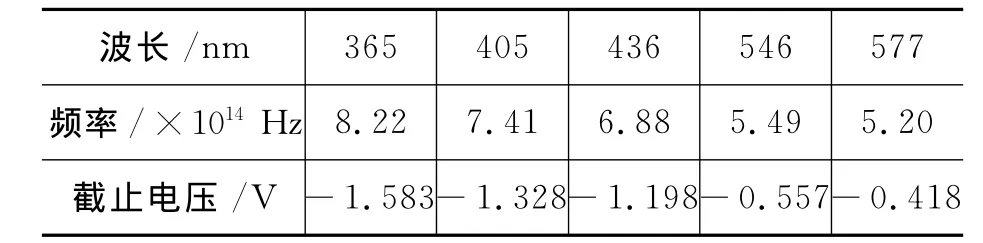
表2 截止电压（取正值）与波长关系

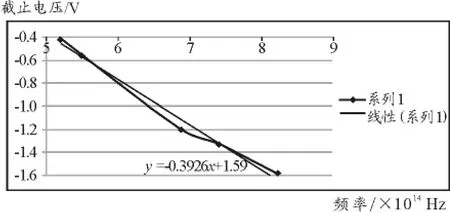
图4

从图4中看出斜率为0.3926，计算得

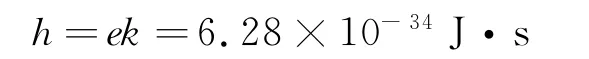
相对误差

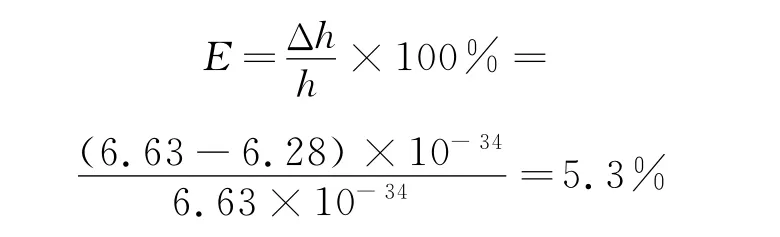
由表2及计算结果可知，本实验通过利用Matlab软件对实验数据进行多次拟合，经过对比发现曲线的三次拟合方程的图形比较符合经验图形要求.故采用三次拟合方程再利用Matlab软件来进行编程计算，其结果误差较小，只有5.3%，可以满足测量普朗克常量要求.经过本次实验，最终证明了曲率法测普朗克常量以及利用Matlab软件进行数据处理的可行性，为实验者提供了快速、准确的数据处理方法.

1 竺江峰，芦立娟，鲁晓东.大学物理实验.北京：中国科学技术出版社，2005.212～219

2011－03－17）