发动机连杆的有限元分析及结构优化
2011-01-19阮帅帅谭丕强崔淑华
阮帅帅,谭丕强,崔淑华
(1. 同济大学 汽车学院,上海 201804;2. 东北林业大学 交通学院,哈尔滨 150040)
发动机连杆的有限元分析及结构优化
阮帅帅1,谭丕强1,崔淑华2
(1. 同济大学 汽车学院,上海 201804;2. 东北林业大学 交通学院,哈尔滨 150040)
本文运用ANSYS Workbench 2.0对N485柴油机连杆进行仿真计算,对极限工况下的应力分布进行分析,并在此基础上采用DOE优化技术对其结构实施优化,计算所得数据,可为厂家改进连杆设计提供参考。
连杆;ANSYS Workbench;有限元分析;优化设计
0 引言
随着能源问题日益加剧,从降低油耗的角度出发,要求汽车朝轻量化方向发展,其中,发动机轻量化已成为整车开发中一个不可忽视的问题。基于发动机轻量化考虑,须对其主要零部件实施优化,以减小体积,减轻质量。连杆作为发动机中受力最复杂的部件之一,如何使之重量轻、强度高,成为现代发动机设计中争相突破的目标。本文应用ANSYS Workbench 2.0(下文简称AWE)对N485柴油机连杆进行仿真计算,研究它在极限工况下的应力分布状况及危险区域,并在此基础上对其结构实施优化。
1 连杆受力分析
连杆在工作中受力复杂,基于动静法分析,主要受到活塞作用力、连杆惯性力、曲轴作用力及螺栓预紧力的作用。在惯性力系下,气体力与活塞组往复惯性力矢量叠加后,形成活塞作用力传至连杆。当连杆存在摆角时,活塞作用力在连杆小头孔内分解为沿杆向的作用力和垂直于缸壁的侧压力。此时气缸壁还给活塞一个与侧压力等大反向的作用力,因而传到连杆上的力就只有杆向作用力。由于工作时,连杆既随活塞作平移运动,又绕活塞销相对摆动,且运动状态不断变化,所以它还存在往复惯性力、离心惯性力及惯性力矩。根据达朗贝尔原理,曲轴对连杆的作用力与活塞作用于连杆的力,连杆往复惯性力,连杆离心惯性力及产生连杆惯性力矩的力,在形式上构成平衡力系。此外,由于本文是将连杆杆身与连杆盖作为研究对象,因此,除上述作用力外,连杆还受到螺栓预紧力。工作中的连杆运动状态呈周期性改变,在进行有限元分析时,主要考虑标定工况下连杆所处的两种极限情况:最大拉伸工况和最大压缩工况。其中,最大拉伸工况出现在活塞接近排气行程终了上止点时,连杆所处的工作状况;最大压缩工况取气缸最大爆发压力下,连杆所处的工作状况[1]。
2 连杆有限元分析
2.1 建模分析
本文在静力分析模块下对N485柴油机连杆进行仿真,并在AWE的DesignModeler模块进行建模。建模通常有三种思路:1)基于同一坐标面建立所有草图,通过控制拉伸量实现连杆厚度的不同(模型线条重叠,参数无法指定);2)在不同平面创建各草图并用倒圆命令处理杆身与大、小头间的圆弧过渡区(计算参数过多,运算时间太长);3)建出连杆在摆动面及垂直摆动面方向上的截面草图,再用扫略命令切出圆弧过渡区。最终选定思路三进行建模,此法所建模型更接近实物,且所需指定的优化参数较少,优化耗时也较少,约五个小时。在定义材料(材料见下文)后,系统算出该连杆模型的质量为1127.7g,与实际所选的N485连杆质量1122.0g相比,完全满足计算精度要求。由于本连杆在摆动面方向对称,所以取1/2厚度的模型进行计算,这样,不仅反映了连杆的实际受力,而且可以提高运算速度,缩短计算时间,还能节省大量的内存,用以细化网格划分,提高计算精度。
2.2 定义材料
为了保证连杆在结构轻巧的条件下有足够的刚度和强度,N485 连杆采用具有良好使用性能的中碳合金钢40Cr,其参数[2]如表1所示。
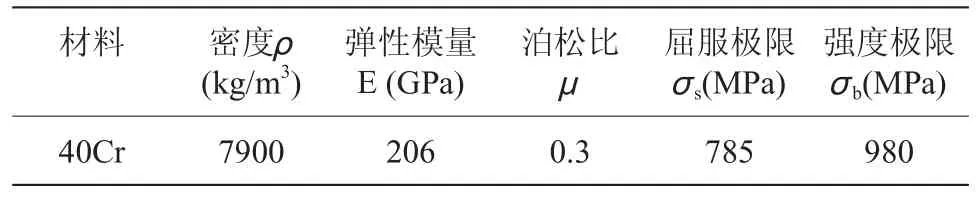
表1 材料参数表
2.3 网格划分
建模后须对模型进行网格划分。AWE不仅具有功能强大的网格划分工具,还能进行智能化网格划分,生成形状特性较好的单元来保证网格质量,给使用者节省了大量的时间和精力。一般情况下,采用默认网格控制即可。有时,为了获得高质量的网格,也可通过一定的控制使其尽量符合有限元计算的要求,提高计算精度。根据所建模型,本文比较了四种不同网格尺寸对计算结果的影响,在完全采用默认控制的情况下,连杆上的最大压应力为254.08MPa(误差偏大);当网格尺寸为0.0026m时,最大应力为277.62MPa(误差趋小);将网格再细化到0.0013m时,最大应力值为287.92MPa(误差更小);当网格细到0.00065m时,系统显示内存不足,分析自动停止。兼顾精度要求及计算机的配置内存,本文最终选定尺寸为0.0013m的网格,共划分出51069个单元,90014个节点,如图1所示。
2.4 AWE中的连杆边界处理
2.4.1 施加载荷

图1 网格划分后的实体模型
2.4.2 约束处理
边界约束可消除整体模型的刚性位移和确定位移函数在边界上的初始条件。本文在最大压缩工况下,把杆身上的半个大头孔圆柱面进行全约束;在最大拉伸工况下,对杆盖上的半个大头孔进行全约束。此外,由于选用的是对称的1/2模型,所以在其对称面上还须施加对称约束。
2.5 强度分析
一般来说,对于钢、铜、铝等塑性材料,可根据第四强度理论,选用Von Mises等效应力进行强度校核[4]。
1)在最大压缩工况下,应力集中区主要分布在N485连杆杆身上,其中,最大应力出现在小头与杆身连接的圆弧过渡区,大小为287.92MPa。因40Cr的许用应力[σ]=785MPa,大于287.92MPa,折合成安全系数为2.73,故在最大压缩工况下,连杆满足强度要求。
2)在最大拉伸工况下,N485连杆的应力集中区在连杆杆身与连杆盖的结合面上,属于较薄弱的部位,最大等效应力值为173.95MPa,远低于785MPa,折合成安全系数是4.51,因此,在最大拉伸工况下,连杆也满足强度要求。
2.6 疲劳分析
由于连杆在工作中一直受不对称的交变循环载荷作用,须进一步从疲劳强度角度来评价其安全性。根据文献 [5],可用Von Mises等效应力将复杂的应力状态转化为具有相同效应的单向应力状态,并视最大拉伸工况下的等效应力为单向拉应力,最大压缩工况下的等效应力为单向压应力。这样,只需从有限元强度分析结果中提取感兴趣点的等效应力值,便可求解连杆的疲劳安全系数。本文选择最大压缩工况下的最大应力点作为危险点进行疲劳校核。该点在最大拉伸工况下所对应的等效应力为47.00MPa。根据疲劳计算公式可得该连杆的疲劳安全系数为2.18,落在1.5~2.5范围内[6],满足疲劳强度要求。
综上分析,本连杆用料偏多,在强度上过于安全,尚存一定的优化空间,因此,须对其进行更加合理化的设计。
3 连杆优化设计
3.1 DOE优化技术简介
DOE技术是指基于试验设计(Design of Experiments)的优化技术。它根据设计点的维数以及设计变量的上下限,利用蒙特卡罗抽样技术,采集设计参数样本点,计算每个样本点的响应结果,并利用二次插值函数来拟合该多维解空间,然后根据目标函数求取该函数面的极值[7]。这是一种应用极为广泛的优化方法,可有效预测极值出现的位置,但基于响应面优化得到的结果会存在一定的误差,须对优化后的结构再次仿真分析,以得到准确的响应。本文采用的优化方法就是DOE优化技术。
3.2 优化问题的数学模型
1)在连杆的优化问题上,本文选择连杆质量作为目标函数。
2)确定优化参数。从结构角度分析,因连杆大、小头内径、大、小头厚度以及大、小头孔的中心距均一定,而其余外形尺寸是待定的,所以图2所示的几个主要尺寸参数是可变的。基于连杆建模方式的考虑,本文选取以下参数作为优化变量:P10—小头外径,P11—1/2杆宽,P12—连杆大头外径减去内径的差值,P13—1/2杆厚,P14—1/2凹槽厚,P15—1/2槽宽。
3)本文允许上述6个设计参数在偏离初始值15%的范围内变化,考虑到连杆小头刚度的要求以及连杆的尺寸,取其外径下限值为40mm。

图2 连杆主要参数
4)为保证安全性,通常,机械构件的安全系数为1.3~1.5[8],针对连杆优化问题,本文选择最小安全系数大于等于1.5作为约束条件。
3.3 获取样本点
根据所选的6个设计变量,系统共生成45个样本点,再基于样本点的计算结果,生成响应面,最后从响应面上选出最优的三个设计点作为候选方案,本文选用表2所示优化方案

表2 连杆优化前后尺寸变化表
3.4 优化结果分析
优化后的连杆,其应力分布情况如图3所示。
由图3(a)和(b)可知,最大压缩工况下连杆的最大应力仍出现在小头与杆身连接的圆弧过渡区,大小为369.76MPa,折合成强度安全系数为2.12;最大拉伸工况下的最大应力为177.52MPa,折合成强度安全系数为4.52;取最大压缩工况下的最大应力点为危险点,计算得疲劳安全系数为1.69。由此可见,优化后的连杆无论在最大压缩工况,还是在最大拉伸工况下,它的强度安全系数均大于1.5,疲劳安全系数也大于1.5,因此,满足设计要求。优化后,1/2连杆的质量是0.48kg,与优化前的质量0.56kg相比,减少了14.29%,共0.08kg。
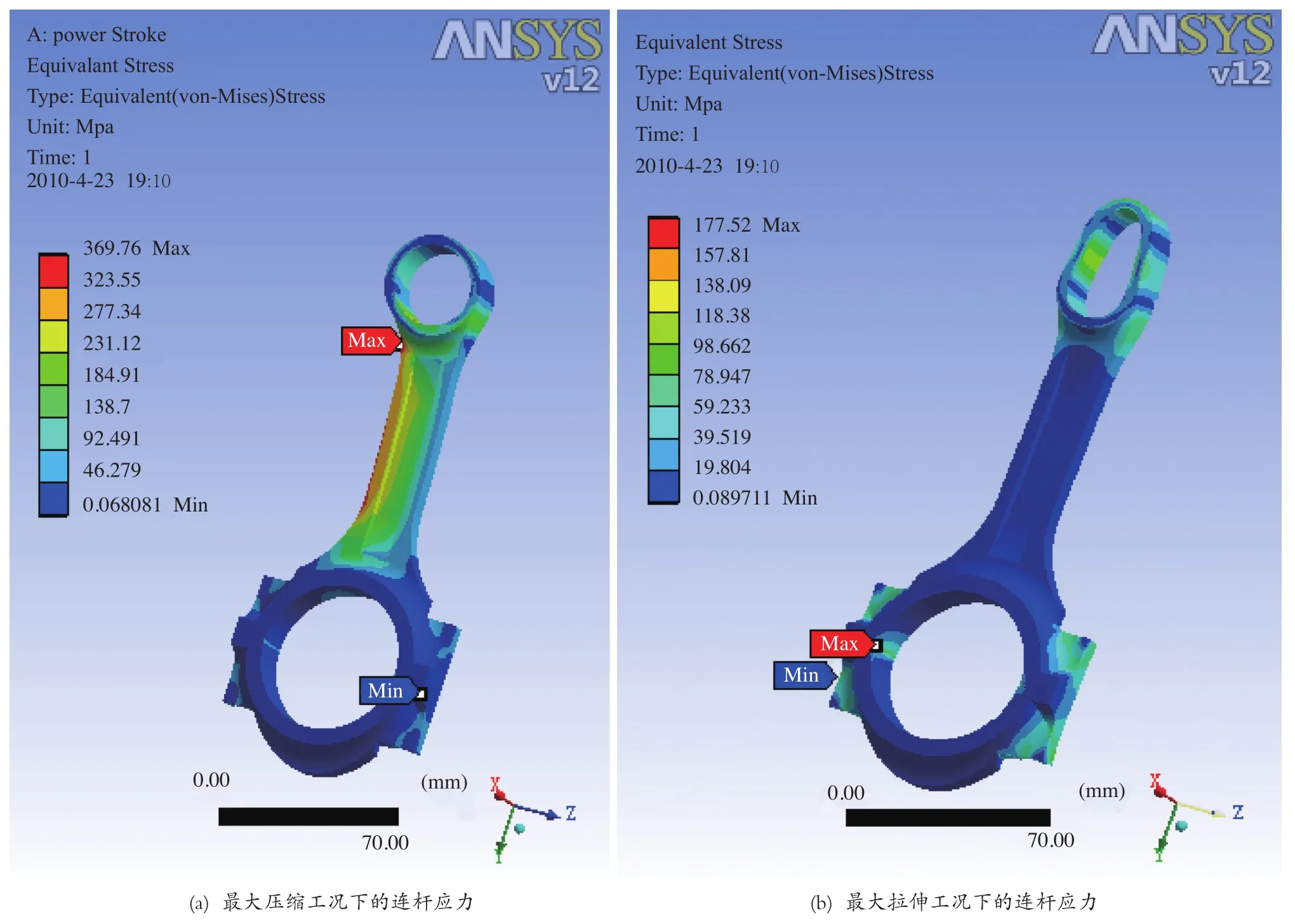
图3 连杆优化后的应力云图
4 结论
本文针对N485柴油机的连杆,运用ANSYS Workbench 2.0对其进行建模和相关分析研究,主要得出以下几点:
1)运用ANSYS Workbench对于N485连杆进行建模需把握得当,经过比较三种建模思路,最后选择以扫略方式切割出连杆凹槽及圆弧过渡区,使所建模型既逼真,又缩短了优化耗时;
2)使用Workbench分析时,须合理划分网格。通过比较四种不同尺寸网格对计算结果的影响,最终选定Element Size为0.0013m的网格。不仅精度较高,又兼顾了计算机的配置和内存;
3)对于N485柴油机连杆的极限工况进行分析,其应力集中区域处于连杆小头与杆身连接的过渡区段,最小强度安全系数为2.73,大于1.5,且其疲劳安全系数为2.18,也大于1.5,因此还存在一定的优化空间;
4)采用多目标优化工具DesignXplorer中的DOE设计模块对连杆的结构进行最佳设计。改进后的连杆在极限工况下的最小强度安全系数为2.12,疲劳安全系数为1.69,均大于1.5,符合设计要求,此时,对于整个连杆共减少质量0.16kg。
[1] 马迅, 胡振华, 张胜兰. 连杆强度和刚度的三维有限元分析[J]. 湖北汽车工业学院学报, 2003:11.
[2] 吴宗泽. 机械设计师手册[M]. 北京: 机械工业出版社,2009: 7-313.
[3] 万欣, 林大渊. 内燃机设计[M]. 天津: 天津大学出版社,1989: 229.
[4] 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2007:245-247.
[5] 夏志皋. 塑性力学[M]. 上海: 同济大学, 1991.
[6] 杨连生.内燃机设计[M].北京:中国机械出版社,1981:252.
[7] 曾祥亮,李力,肖露. 基于ANSYS Workbench的钢模台车优化设计[J].组合机床与自动化加工技术, 2009:103.
[8] 陆际清, 孟嗣宗. 汽车发动机[M]. 北京: 清华大学出版社, 1990.
Finite element analysis and structural optimization of engine connecting rod
RUAN Shuai-shuai1, TAN Pi-qiang1, CUI Shu-hua2
TH132
A
1009-0134(2011)5(下)-0110-04
10.3969/j.issn.1009-0134.2011.5(下).33
2010-12-01
阮帅帅(1986-),女,浙江台州人,硕士研究生,研究方向为汽车发动机现代设计技术。
