一般线性李代数的极大理想

陈丙凯,卞鸿亚,关　琦

(中国矿业大学 理学院,江苏 徐州　221008)

0　引言

理想的研究对于李代数结构的研究有重要意义.近些年来,很多文章已经研究了李代数的结构.值得注意的是,从李代数的理想着手研究李代数结构是比较常用的方法,近年来得到研究者们的重视,也获得了不少研究成果[1-8].如Gauger[1]第一次研究了幂零李代数上的2维中心可换理想. Benito.M.P等[2]证明了L是域上的一个李代数,若L的维数大于1并且L不是单李代数,L有唯一的极大理想Benito.M.P[3]证明了在特征为0的代数闭域和实数域上的可解李代数完全分类并且他们的理想最多是5个.Belitskii.G[4]研究了3维的中心可换理想. Fang C Y[5]研究了一类复杂的单李代数的ad-幂零理想.Bartolone.C在文[6]中完全分类了含有2维非中心可换理想的幂零李k-代数.最近Towers[7,8]研究了在域上的李代数的极大子代数.而研究李代数的极大理想问题得文章都比较少,特别是在环上研究李代数的极大理想的工作很少研究.本文受此启发,给出了在含幺可换环且2和n可逆上的一般线性李代数的完全分类.

现在给出一些定义.假设R是含幺可换环,I是R的极大理想,则我们定义R/I是R关于I的剩余典型域.Mm×n(R)定义为R上的所有m×n阶矩阵的集合.Mn×n(R)缩写成Mn(R).如果括积运算定义成[x,y]=xy-yx,则Mn(R)变成了李代数,我们称它为一般线性李代数用gln(R)来表示.gln(R)有一组包含矩阵eij的标准基,其中eij表示在(i,j)处是1其他处全是0的矩阵.因为eijekl=δjkeil,所以[eij,ekl]=δjkeil-δliekj.现在假设当i≠j时,Eij=eij,

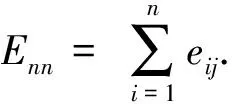
1　预备知识

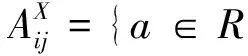
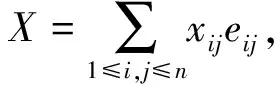
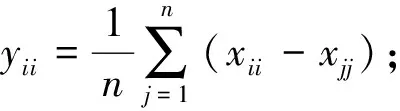
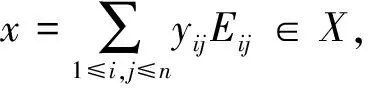
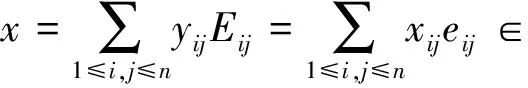
因为

因此

这时有

[(xii-xjj)(eii-ejj),eii+1]=(xii-xjj)eii+1∈X,

所以

[(xii-xjj)eii+1,ei+1i]=(xii-xjj)(eii-ei+1i+1)∈X.

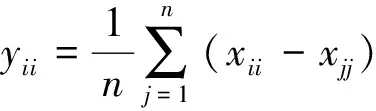
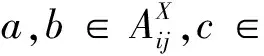
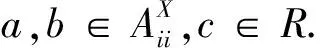
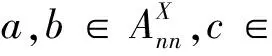
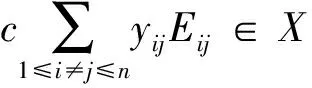
现在我们构造两类关于gln(R)的极大理想．假设R是含幺可换环且在2和n处可逆,I是R的极大理想.

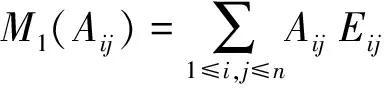
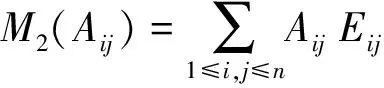
3　 主要结果

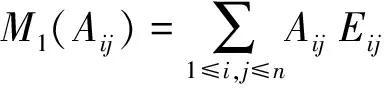
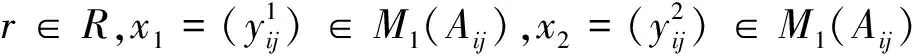
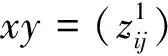
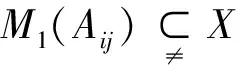
若当p=q使得ypp∉I.我们由引理1知,有yppEpp∈X.所以[ypp(epp-ep+1p+1),epp+1]=2yppepp+1∈X.而我们由前面得证当p≠q时,有X=gln(R).

因此综上可得M1(Aij)是gln(R)一个极大理想.证毕.

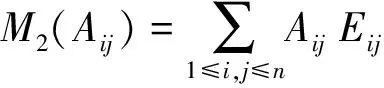
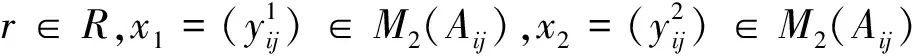
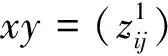
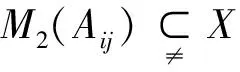
下面这个定理考虑当R是一个域上时,我们给出了gln(R)所有的极大理想.

定理1假设R是一个域且在2和n出特征不为0.则X是gln(R)的极大理想当且仅当X=sln(R)或者X=φ(R).其中sln(R)表示包含所有迹为0的n×n阶矩阵的集合,φ(R)表示包含所有n×n阶纯量阵的集合.

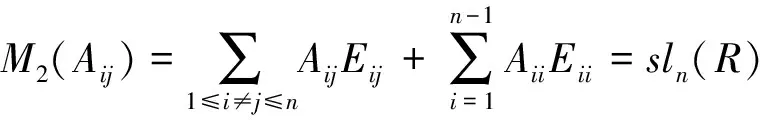
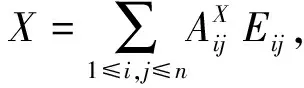
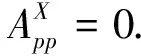
若当p=q=n时,X⊆sln(R).由X是gln(R)的一个极大理想,所以当p=q=n时,X=sln(R).证毕.

下面这个定理考虑当R是一个含幺可换环上时,我们给出了gln(R)所有的极大理想.

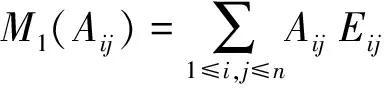
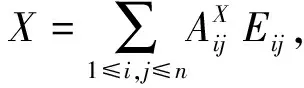
应用定理2,当(p,q)≠(n,n),σ(X)=AnnEnn=φ(R),这里Ann=R.应用σ-1我们得到

X+gln(I)=AnnEnn+gln(I)=φ(R)+gln(I).事实上AnnEnn+gln(I)=φ(R)+gln(I)就是M1(Aij).所以我们得到X⊆X+gln(I)=M1(Aij).由假设知X是gln(R)的一个极大理想,所以当(p,q)≠(n,n)时,我们得到X=M1(Aij).

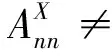
反例1

在假设n≥3,R是含幺可换环且的特征是n.

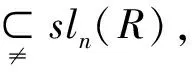
参考文献：

[1]Gauger M. On the classi-ation of metabelian Lie algebras[J]. Trans Amer Math Soc,1973,179:293-329.

[2]Benito M P. Lie algebras in which the lattice formed by the ideals is a chain[J]. Comm Algebra,1992,20(1):93-108.

[3]Benito M P. Lie Algebras With a Small Number of Ideals[J]. linear algebra and its applications,1992，177: 233-249 .

[4]Belitskii G,Lipyanski R,Sergeichuk V V. Problems of classifying associative or Lie algebras and triples of symmetric or skew-symmetric matrices are wild[J]. Linear Algebra Appl,200,407:249-262.

[5]Fang C Y. Ad-nilpotent ideals and equivalence relations[J]. Journal of Algebra,2010,323:2016-2025.

[6]Bartolone C,Di Bartolo A,Falcone.G Nilpotent Lie algebras with 2-dimensional commutatorideals[J]. Linear Algebra and its Applications,2011,434:650-656.

[7]Towers D A. Maximal subalgebras of Lie algebras containing Engel subalgebras,arXiv:1004-5005v1[R]. 28 Apr,2010.

[8]Towers D A,Supplements to maximal subalgebras of Lie algebras,1007-4902v1[R]. 28Jul,2010.