高填土路堤沉降计算方法分析

张占荣,刘庆辉,杨艳霜,谭家华

(1.中铁第四勘察设计院集团有限公司,武汉 430063；2.中国科学院武汉岩土力学研究所,武汉 430071)

1 概述

近十几年来,随着我国铁路、公路建设事业的飞速发展,线路修建的等级和质量也相应提高。为了保障高等级线路的平顺性,当线路跨越深沟、穿过地面障碍或修筑高桥引道时,均可能采用高填土路堤方案通过,线路等级的提高,对路堤沉降也有了更高的要求。因此,在路堤设计、施工过程中,有必要对路堤自身沉降进行预估,以便在路堤终验时达到设计高程[1-2]。

路堤及其各部分处在自重荷载、行车荷载及许多自然因素作用之下,高填方路堤由于堤身较高,填料自重应力较大,行车荷载与路堤自重相比,一般是不大的。填料自重应力引起的堤身自身沉降、不均匀沉降以及地基沉降较大,由此引起的工程问题,轻则是路面过早破坏,影响正常交通运输和行车安全,重则由于过大沉降而导致路堤失稳,造成路堤毁坏,中断交通运输,甚至危及生命安全。以往的研究往往只关注路基的沉降,而忽视了路堤本身压缩沉降,且在各种设计手册中还没有建立计算路堤本身压缩沉降量的统一公式。因此,在高等级公路、高速铁路的高填方路堤设计中,路堤沉降计算问题亟待解决。

本文在前人工作[1]的基础上,提出了基于土体割线模量的改进分层总和法。该方法考虑了不同应力状态下土体变形参数的差异,即结合室内土工试验成果,获取土样在不同应力状态下的割线模量,并考虑路堤填土的分层填筑特性、填筑完成后土体应力状态,从而使得分层总和法能够更适用于路堤沉降计算领域。以某高填土路堤为例,并结合土工试验成果,综合分析了分层填筑过程中路堤在自重作用下的沉降特征,获得该填土路堤的沉降计算结果。为了进一步验算该计算方法的可靠性,进一步建立了三维数值分析模型,采用植入到FLAC3D中的邓肯-张非线性本构模型,对其进行了分析。对比分析表明,理论方法与数值分析方法沉降计算结果基本一致,表明该方法可以作为评价路堤沉降的一种简便方法加以应用和推广。

2 路堤沉降计算的改进分层总和法

2.1 土体变形特性

分层总和法物理意义简单明确,所需计算参数容易获取,是目前较为简捷的沉降计算方法,在工程实践中得到了广泛应用。该方法在计算过程中所需参数一般是压缩模量ES,或者变形模量E0。压缩模量ES为一个与应力水平有关的量,可通过室内固结试验获取,计算公式如下[3]

(1)

式中，e0为试样的初始孔隙比；av为某一压力范围内的压缩系数,可表示为

(2)

式中，pi、pi+1为固结试验采取的各级压力值；ei、ei+1为各级压力下试样固结稳定后的孔隙比。

通过换算,即可得到用应力、应变表示的ES的表达式(图1)

(3)

式中，σi、σi+1为固结试验各级压力下试样的应力值；εi、εi+1为各级应力下试样固结稳定后的应变值；Δσ、Δε为两不同级压力下试样的应力差、应变差。

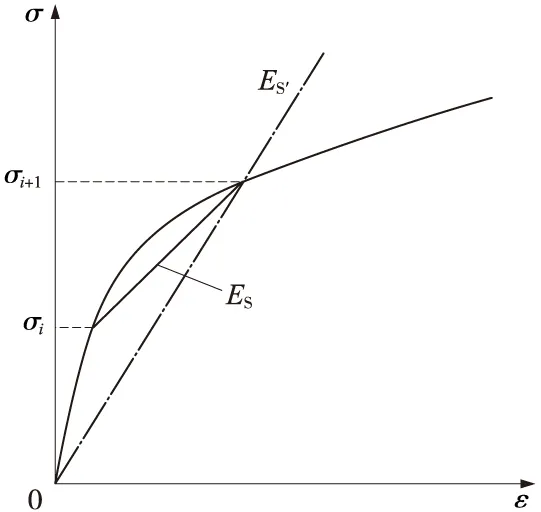
图1 压缩模量与割线模量的定义

地基工程沉降计算中,存在竖向初始应力σz0,地基沉降主要是由于竖向附加应力σzi的作用导致,因此选取压力段(σz0～σz0+σzi)计算得到的ES,能很好地反应地基土在附加应力下的变形特性,相关规范[4]也是采用此原理进行地基沉降计算的。

2.2 髙填土路堤工程与一般地基工程的差异

在一般的研究中,往往忽视了路堤工程与地基工程的差别,在沉降计算上仍采用传统的分层总和法。但是对于路堤工程沉降计算时,与地基工程存在着两点显著区别。

(1)地基沉降是附加应力作用下导致的地基变形；而路堤沉降则主要为路堤填土在自重荷载下的变形所致,对于高填土路堤来说则更为显著。

(2)由于扩散效应,土中的附加应力由上向下逐渐减小,土体变形量也是由上向下逐渐减小,导致地基变形由上向下呈现高度的非线性减小趋势；而路堤沉降计算则需要考虑填土分层填筑的先后顺序。每层路堤填土在刚填筑时沉降为零,后续填土的重力荷载导致了该层填土的沉降变形,一般最大沉降量位于路堤三分之一高度的位置。

由于上述差异,路堤沉降计算过程中,土体变形参数的选取与地基沉降计算是有所不同的。假设路堤填土完成时,某一点的竖向应力为σZ,则在填筑开始到填筑完成的过程中,该点的应力状态变化范围是0～σZ,故应采用此应力范围确定的土体变形参数,如图1所示,在图中表现为经过原点的直线的斜率,在此称之为割线模量ES′,在计算路堤沉降的过程中,均应采用与所处位置竖向应力状态有关的割线模量。考虑到路堤填土填筑完成后受到侧向压力约束,室内估计试验是一种限制侧向变形的侧限压缩试验,不能计算围压的大小,在此应采用土体三轴压缩试验曲线,考虑路堤填土实际状态围压的大小来选取合理的割线模量ES′。

2.3 髙填土路堤沉降计算

针对路堤分层填筑特性,对路堤沉降的计算公式进行推导,计算模型如图2所示。

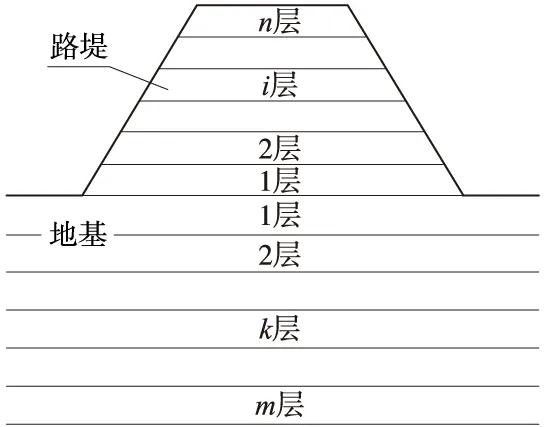
图2 分层总和法计算模型

假设路堤填筑完成后,第i层路堤填土最终沉降量SiT为其上部填土在该层产生的应力作用下,也就是路堤填筑完成时该层的竖向应力作用下,其下部路堤填土和地基的变形总和,可按下式计算

SiT=SiE+SiS

(4)

式中，SiE、SiS分别为路堤填筑完成后在第i层竖向应力作用下,其下部路堤填土、地基的变形。

路堤填筑完成时,其内部某一点的竖向应力σz近似等于该点以上土柱的重力[5],即

σz=γh

(5)

式中，h、γ分别为该点以上土柱高度、重度。

结合图2可知路堤填筑完成时,第i层土条中的平均竖向应力σzi为

(6)

由于每层路堤刚填筑完成时,该层并没有产生沉降,故在路堤填筑过程中,每层路堤刚刚填筑完成时,该层的沉降量应该为零。所以第i层填土的最终沉降量,可表示为其上填土在该层产生的竖向应力的作用下,也就是路堤填筑完成时该层的竖向应力作用下,本层及其下部路堤填土变形的总和。故它的最终沉降量SiE可以表示为

(7)

式中，σzi为路堤填筑完成时,第i层土条的平均竖向应力；Esj为室内试验中,对应于第j层土条的围压,是在应力段(0～σzj)的割线模量。地基变形部分可按传统分层总和法计算。由于路堤内部的竖向应力σz近似为该处上部土柱产生的重力,计算第i层填土的最终沉降量时,地基附加应力可按梯形荷载BCED来进行计算,具体为三角形荷载ABC减去ADE之差的作用结果,如图3所示。

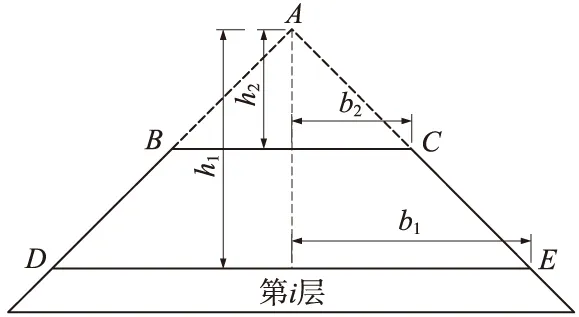
图3 地基附加应力计算时考虑的荷载

地基在等腰三角形荷载作用下,中心线下竖向附加应力可由下式计算[6]

(8)

式中，z为计算点深度；q为荷载最大值的集度；b为荷载半宽度。

由式(8)可得图3荷载作用下,地基附加应力计算公式

(9)

据分层总和法原理,第i层填土最终沉降量中,地基变形部分为

(10)

式中，σzk、Esk、Sk分别是地基中第k层土条的竖向附加应力、相应压力段的压缩模量、计算沉降值,Δh为考虑的土条厚度。

沉降计算的深度一般应符合《建筑地基基础设计规范》(GB50007—2002)的规定

(11)

式中，Sm为在计算沉降深度向上取厚度为Δh的土层变形值；Δh的选取可参考《建筑地基基础设计规范》(GB50007—2002)；Sk为在沉降计算时,第k层土的计算沉降量。

综上分析，可以得到路堤第i层填土的最终沉降表达式

(12)

3 工程实例分析

3.1 工程概况

拟建某公路全长54.67 km,连接张家界与桑植,总投资4.3亿元,为山岭重丘二级公路。其中桩号K34+900 m～K35+150 m路段采用填土路堤形式,最大路堤填筑高度约有30 m。

3.2 数值分析方法及计算结果

本次数值分析采用FLAC3D程序,该程序于20世纪90年代引入我国,在岩土工程领域得到了广泛的应用[7]。通过该程序预留的UDM程序接口,用户可方便地植入新的本构模型,以满足实际应用的需要。通过FLAC3D程序接口,应用VC.net平台,编制DLL动态链接库文件,使邓肯-张(E-B)模型在FLAC3D程序中得到实现[8～9]。

结合地质资料,建立了数值分析模型,自上而下考虑了碎石土、强风化页岩、弱风化页岩。碎石土厚度为5 m,强风化页岩厚度取20 m。模拟时路堤按照1 m/层填筑,填筑共分为28层。路面及分层面生成时,首先沿道路中心线选一定量的点,根据平曲线、纵曲线信息得到点的空间坐标,路面和分层填筑面分别沿着由这些点生成的样条曲线延伸,形成接近工程实际的空间曲面。由此生成了三维计算模型,见图4。

据工程地质勘察及室内试验成果,地基岩土体采用摩尔-库仑本构关系,计算参数见表1。路堤填土采用邓肯-张本构模型,根据室内土工试验成果计算获取,见表2。

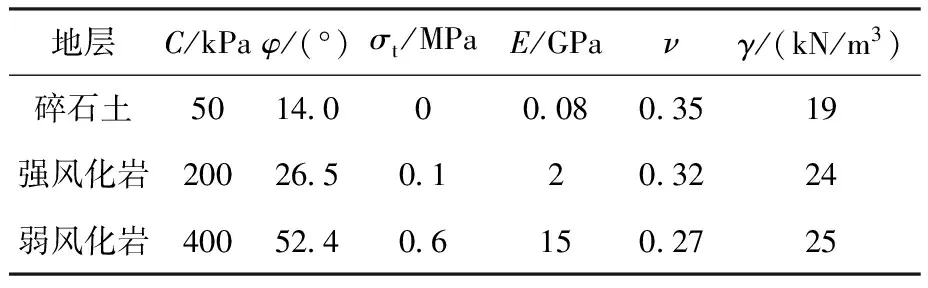
表1 地基土体力学参数

表2 路堤填土力学参数

通过计算分析结果如下。

(1)随着路堤填筑高度的增加,路堤表层沉降逐渐增大；路堤填筑完成后,表层沉降最大沉降量约为13.1 cm,位于路堤侧面中心部位。路堤侧向变形表现为向两侧变形,受地形地貌影响较大,侧向变形为零的线从路堤顶面穿过,但并未与道路中心线吻合；填筑完成时路堤表层最大侧向变形约为3.0 cm。受地形地貌影响,路堤填土出现一定量的轴向变形,路堤填筑完成时,表层最大轴向变形约为2.6 cm。

(2)随着路堤填筑高度的增加,路堤内部沉降和侧向变形逐渐增大。路堤内部最大沉降约位于填筑面剖面中点下方、填筑高度1/3的位置,填筑完成时路堤内部最大沉降量为51.0 cm。路堤内部侧向变形表现出向两侧变形的趋势,路堤填筑完成时,侧向变形为零的线近似从路堤填土中线附近穿过,最大侧向变形发生在路堤剖面填土中线与路堤侧面中间、填土高度约1/3的部位。路堤轴向变形主要是受地形地貌和涵洞的影响,轴向变形较大位置主要位于路堤与原地面线接触附近。

3.3 分层总和法及对比分析

路堤填土在不同的应力状态下,压缩模量不同；由土工试验所得的路堤填土在不同围压条件下的压缩特性见图5。假设路堤填土中心线上侧压力系数由自重应力产生,假设填土的泊松比为0.35,则侧压力系数约为0.5。在计算路堤沉降时采用割线模量,通过对图5中的数据整理得到路堤填土在各个应力状态的割线模量参数见表3。

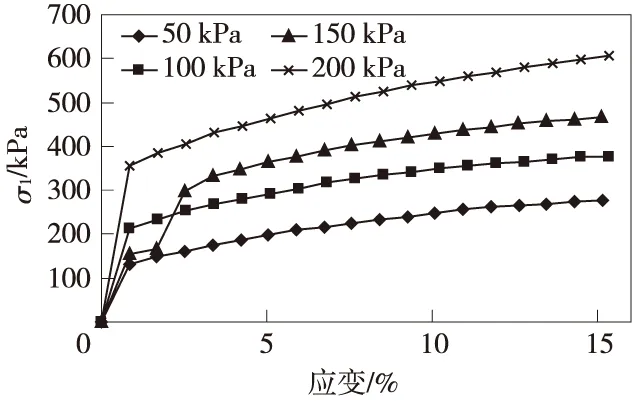
图5 路堤填土不同围压下的压缩特性曲线

表3 不同应力水平下路堤填土的割线模量

选取桩号K35+033剖面,采用改进分层总和法进行路堤沉降计算,与数值模拟方法结果对比列于图6。

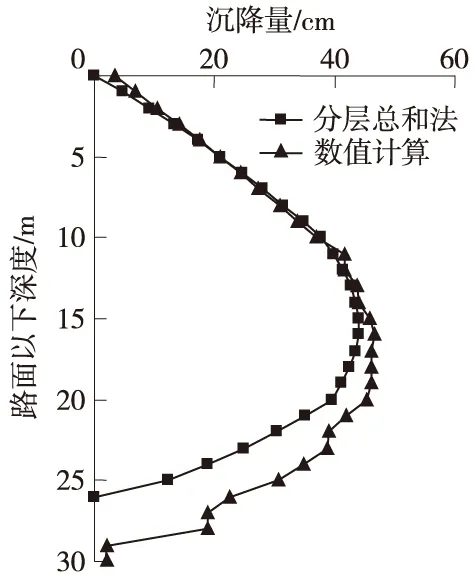
图6 计算结果对比

两种方法所得路堤沉降在趋势上基本吻合,最大沉降量均位于路堤填土高度1/3左右的位置,由于分层总和法没有考虑实际地形地貌对沉降的影响,在接近地表附近计算差别较大。本文推导的路堤沉降计算公式步骤简单、所需参数少、不需要建立数值分析模型,故在原地表倾斜不大时作为计算填土路堤沉降的简便方法。

4 结论

(1)结合路堤填筑过程中填土分层填筑的时间先后特性,考虑土体填筑完成后的实际应力状态来选取较为合理的土体割线模量,推导了路堤沉降分析的改进分层总和法计算公式。该公式较以往的成果考虑更加成熟,更加接近路堤工程的实际情况,因此获得的结果更加实际有效。

(2)针对一高填土路堤工程,采用植入到FLAC3D中的邓肯-张非线性本构模型,对其进行了沉降分析,与本文推导的理论方法计算结果进行对比分析,表明本方法简单可行,可作为评价路堤沉降的一种简便方法加以应用和推广。

[1]张占荣,盛谦,朱泽奇,等.路堤沉降分析的修正分层总和法研究[J].长江科学院院报,2010,27(3):50-53.

[2]罗喜元.石灰改良下蜀黏土作为高速铁路路堤填料的工程性质试验研究[J].铁道工程学报,2008,8:6-9.

[3]高大钊,袁聚云.土质学与土力学[M].3版.北京:人民交通出版社,2006．

[4]GB50007—2002，建筑地基基础设计规范[S].

[5]陈慧远.土石坝有限元分析[M].南京:河海大学出版社,1988．

[6]Poulos H G, Davis E H. Elastic solutions for soil and rock mechanics[M]. John Wiley and Sons, New York, N. Y., 1975．

[7]Itasca Consulting Group, Inc.. Fast Language Analysis of continua in 3 dimensions, version 3.0, user’s manual[R]. Itasca Consulting Group, Inc., 2005．

[8]冷先伦,盛谦,朱泽奇,等.邓肯-张模型在FLAC3D中的实现及工程应用[J].建筑科学,2009,25(1):100-105.

[9]陈育民,刘汉龙.邓肯-张本构模型在FLAC3D中的开发与实现[J].岩土力学,2007,28(10):2123-2126.