LZ地区致密砂岩储层裂缝综合预测方法及应用

王志萍，秦启荣，苏培东，范晓丽

（1.西南石油大学资源与环境学院；2.中国石化中原油田勘探开发科学研究院）

LZ地区致密砂岩储层裂缝综合预测方法及应用

王志萍1，秦启荣1，苏培东1，范晓丽2

（1.西南石油大学资源与环境学院；2.中国石化中原油田勘探开发科学研究院）

LZ地区储层为低孔、低渗致密砂岩储层，裂缝控制了储层的储渗空间和井的产能。通过对LZ地区的构造特征及演化分析，并结合野外露头资料对裂缝产状进行分期配套，认为该区主要发育横张缝、剪切缝以及断层伴生缝和派生缝等构造成因裂缝。针对以上3种构造裂缝类型，分别采用构造曲率法、古构造应力场有限元模拟法、地震不连续性检测法等对该区不同类型裂缝的分布进行了预测，并采用权重评价方法综合这3种预测成果进行裂缝的综合预测，即建立各预测方法的准确率与其影响因子之间的回归函数，再根据预测方法的准确率确定权重系数，将不同方法的预测成果进行综合权重计算，从而对研究区致密储层的裂缝发育情况进行综合预测，经钻井资料证实其预测效果较好。

裂缝综合预测；构造曲率法；古构造应力场；地震不连续性检测；四川盆地

储层裂缝预测是石油地质界的一个难题，至今还没有一套行之有效的技术方法来解决该问题。目前，裂缝预测方法多种多样，地质方法主要应用岩心裂缝观测描述[1］和野外露头观测描述等；测井方法主要应用裂缝的非均质性在测井曲线上形成的异常（电阻率、密度、声波波形、地层倾角）等来实现[2］；地震方法主要应用多场信息预测技术、多方位地震属性预测裂缝技术、多分量与各向异性检测技术[3］、裂缝边缘检测技术及裂缝非线性预测技术等；数学方法主要应用构造应力场反演法[4-11］、有限单元法、分形几何法[12］、灰色评判法、统计法、神经网络法等。但由于裂缝发育受到岩性、构造应力场、岩层厚度等多种因素的影响，非均质性强，因此每种预测方法均有其局限性。针对LZ地区致密砂岩储层中裂缝特点，笔者提出了一套在地质分析基础上采用构造曲率法、古构造应力场有限元模拟法及地震不连续性检测法等3种裂缝预测方法，将不同方法的预测成果综合在一起，进行权重值计算，从而对各区块裂缝的发育分布作出合理的评价。

1 区域概况

LZ地区位于四川盆地川中隆起北部斜坡带，是川中隆起向川北坳陷延伸的一个低幅度鼻状隆起带的一部分，与梓潼—苍溪鼻状构造带和仪陇—平昌低缓构造带毗邻（图1）。LZ地区构造主要由呈弧状弯曲的挤压性褶皱和旋扭性褶皱组成。中侏罗统千佛崖组储层埋深达2 700～3 000 m，岩性以细粒石英砂岩、细粒长石岩屑砂岩、含钙粗粉砂岩为主，次为介壳砂质灰岩，孔隙度为0.7%～2.5%，渗透率为0.008～0.1 mD，为典型的致密砂岩储层。其储集空间主要为孔隙和裂缝，其中裂缝为油气提供了储集空间，提高了储层的渗流能力。在裂缝发育带渗透率可达60 mD，这对于LZ地区致密砂岩储层获得高产具有重要意义。LZ地区裂缝类型多样，既有构造缝，也有成岩缝，其中以构造缝为主，其倾角主要为15°～45°，裂缝充填程度不高，未充填缝占一半以上。

图1 LZ地区区域构造位置图Fig.1 Regional structural location of LZ area

2 裂缝成因分析

裂缝成因分析是在研究区构造特征及演化研究的基础上，以裂缝构造成因理论模型为指导，利用露头资料对裂缝进行分期配套[13］，最终确定裂缝的形成期次和成因类型。裂缝构造成因分析是储层裂缝综合预测的基础，为合理采用不同的裂缝预测方法提供可靠的依据[14］。

LZ地区发育北东向、北西向和近东西向的褶皱。北东向褶皱是在印支期北东东向隆起背景上发育起来的；燕山运动中后期，在南北向构造挤压作用下，LZ地区形成了一系列近东西向的褶皱；喜山运动期，构造应力的方向由近南北向转变为南偏西向，又形成了一系列北西向的褶皱。所以，LZ地区褶皱主要是在燕山后期和喜山期构造应力作用下形成的。

根据构造成因理论分析认为，伴随2期构造应力形成的裂缝系统主要与挤压褶皱作用和断层破裂作用有关。在燕山中后期南北向挤压作用下形成的裂缝，主要为北东向与北西向平面“X”型剪切缝和近东西向的剖面“X”型剪切缝；在喜山期北东向挤压力作用下形成的裂缝，主要为近南北向和近东西向的平面“X”型高角度剪切缝及北西向剖面“X”型剪切缝；在喜山期北东向应力的挤压作用下，燕山期形成的北东向剪切缝开启并形成横张缝且规模变大；燕山期北西向裂缝和喜山期北东向裂缝在构造应力的持续作用下发育为断裂。

根据露头资料对裂缝产状的分析表明，LZ地区裂缝走向以北西向为主，北东向、近南北向、近东西向裂缝次之（图2），裂缝以中—低角度缝和垂直缝为主（图3）。构造成因分析与裂缝类型进行对比认为：研究区发育燕山期北西向平面“X”型剪切缝、喜山期北西向剖面“X”型剪切缝、断裂的派生缝和伴生缝，横张缝局部地区发育，其它类型裂缝发育程度较低。

图2 LZ地区裂缝走向玫瑰花图Fig.2 Rose diagram of fracture strike in LZ area

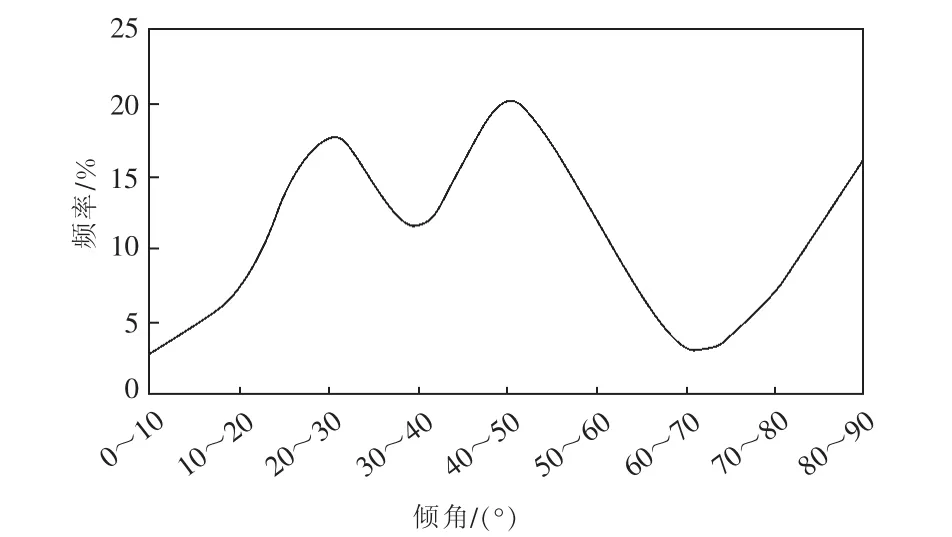
图3 LZ地区野外裂缝倾角统计Fig.3 Statistics of fracture dip in LZ area

3 裂缝预测

在裂缝成因类型分析基础上，针对性地选择构造曲率法、古构造应力场有限元数值模拟法以及地震不连续性检测法来综合预测裂缝的分布。构造曲率法主要预测横张缝分布；古构造应力场有限元数值模拟法主要预测剪切缝的分布；地震不连续性检测法主要预测断层伴生缝及派生缝的分布。

3.1 构造曲率法

由于曲率值可以反映弯曲岩层面上弯曲派生的抗张应力形成的张性缝，因此可利用构造曲率法来预测张性裂缝的分布。本次主要采用了趋势面拟合法来计算千佛崖组储层的相对曲率值，预测结果（图4a）中，Ⅰ级裂缝发育区曲率值为22～31，裂缝发育程度好；Ⅱ级裂缝发育区曲率值为13～21，裂缝发育程度中等；Ⅲ级裂缝发育区曲率值为1～13，裂缝发育程度差。千佛崖组储层曲率值总体较小且分布不均匀，大部分地区曲率值小于4，说明张性缝在大部分地区不发育，仅在局部地区发育，如石龙场构造区。这与研究区整体构造变形强度不太相符。

3.2 古构造应力场有限元数值模拟法

古构造应力场有限元数值模拟法是在分析构造特征和演化史基础上建立地质模型，综合考虑储层的岩性、厚度、岩石力学参数等，以有限元法建立数学模型，并以摩尔-库伦准则为依据，计算岩石破坏接近程度，从而判断储层的岩体破裂程度，同时结合岩心资料和测试资料等对裂缝分布进行预测。在模拟中，用岩石破坏接近程度η值来表示岩体破裂的相对程度，也就是裂缝的发育程度。一般说来，η值越大，裂缝就越发育。目前，国内外通过古构造应力场来研究储层裂缝发育程度还没有统一的判别标准，所以，η值的选取主要是根据多年来在四川盆地的研究结果，并结合LZ地区构造特征和已有的生产资料来确定。预测成果图（图4b）中，红色区域为Ⅰ级裂缝发育区，η值为1.203～1.303，岩体破裂发育，裂缝发育程度好；黄色区域为Ⅱ级裂缝发育区，η值为1.125～1.203，岩体破裂较发育，裂缝发育程度中等；浅黄色区域为Ⅲ级裂缝发育区，η值为1.022～1.125，为岩体破裂发育临界区，裂缝发育程度差。与生产井的资料进行对比可知，高产井一般位于预测结果的Ⅰ级和Ⅱ级区，而一般的生产井位于Ⅱ级和Ⅲ级区，Ⅲ级区主要是一些中低产井或干井。

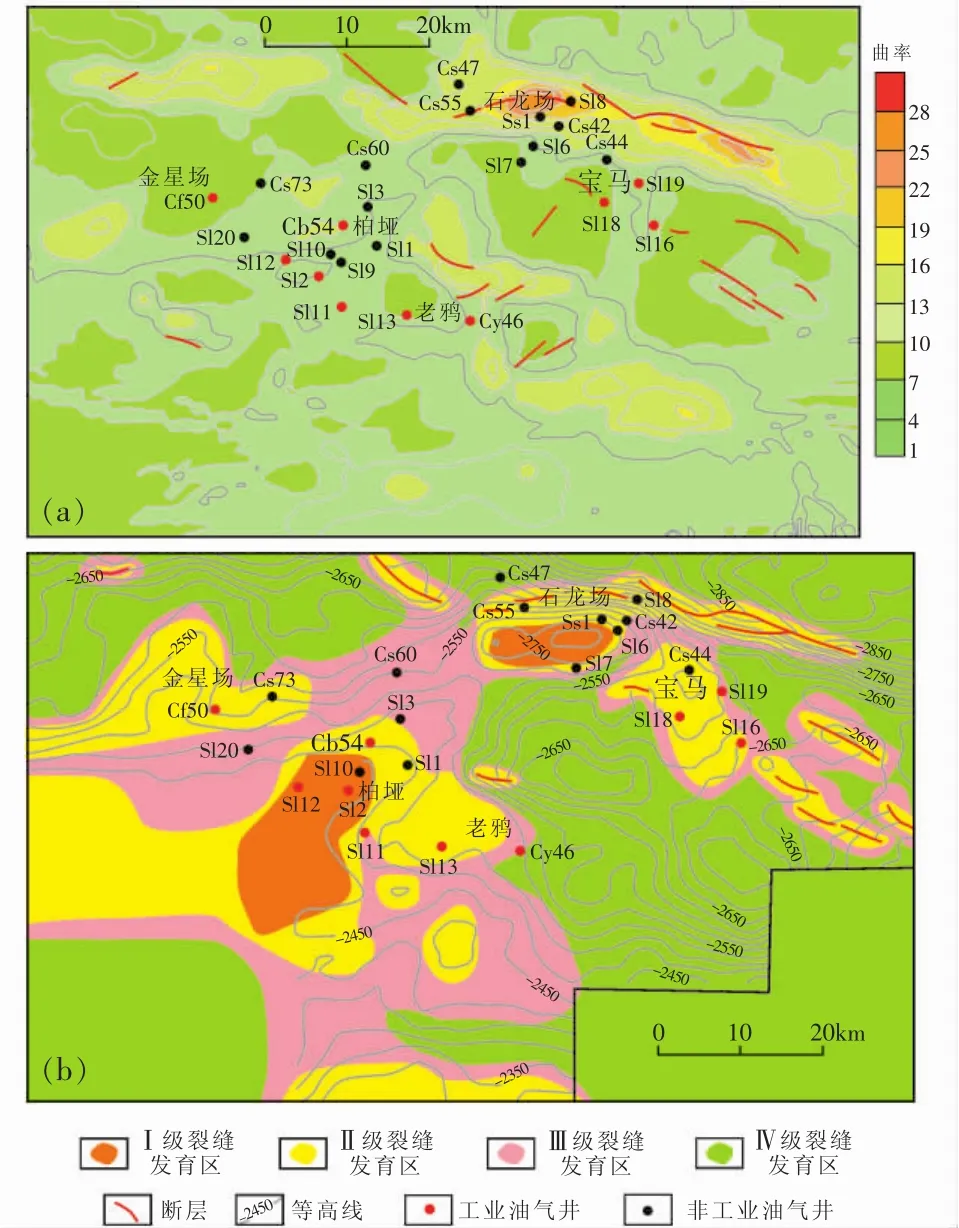
图4 千佛崖组裂缝预测平面图Fig.4 Fracture distribution prediction of Qianfoya Formation

3.3 基于局部构造熵的地震不连续性检测法

基于局部构造熵的地震不连续性检测法分析技术，是运用相关性原理突出相邻道之间地震信号的不连续性，进而达到检测断层和反映地质异常特征展布为目的[15］。具有相同反射特征（振幅、频率、相位）的区域呈相似性，相关值接近1，而在断层、岩性变化的突变点则呈非相似性，相关值接近0。根据相关值高低的空间变化，能快速识别出断层与裂缝的发育带。因此，地震道之间信号相关值的大小是判别断层或裂缝发育带存在的一个重要标志。对本次地震偏移资料进行不连续性处理，并针对处理后的数据体提取千佛崖组时间范围内的平均值，以检测层段内部地震信号的不连续性，从而进行裂缝预测。该方法对断层以及断层附近的裂缝检测效果较好。图5为千佛崖组不连续性平均值平面分布图，红色表示不连续性高值，为Ⅰ级裂缝发育区，裂缝发育程度好；黄色表示不连续性中值，为Ⅱ级裂缝发育区，裂缝发育程度中等；蓝—绿色表示不连续性低值，为Ⅲ级裂缝发育区，裂缝发育程度最差。从图中可以看出不连续性高值主要分布在工区中部，表明断层与裂缝发育，地震不连续性检测法的预测结果与古构造应力场有限元数值模拟法预测结果一致。

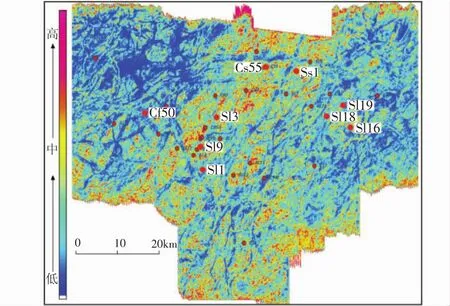
图5 千佛崖组不连续性检测平均值平面分布图Fig.5 Plane distribution of average value of seismic discontinuity detection of Qianfoya Formation

4 裂缝综合预测及效果分析

4.1 裂缝综合预测

储层裂缝综合预测主要由综合构造曲率法、古构造应力场有限元数值模拟法以及地震不连续性检测法这3种预测方法的成果得来的。基于构造曲率法原理，其预测的裂缝主要为张性缝；地震不连续性检测方法由于地震分辨率低，预测的裂缝多为规模相对较大的裂缝或小断层，而对规模较小的裂缝响应较差；古构造应力场有限元数值模拟法受模拟过程中岩石力学参数取值、边界条件等诸多因素的影响，主要预测的裂缝为剪切缝。因此各种方法均有一定的局限性。根据各预测成果的准确程度，设定不同的权重系数，对不同预测成果进行权重分析，从而对各区块裂缝的发育分布作出合理的评价。数学模型为：y=a1X1+a2X2+a3X3。式中，y可看作是总体测评目标；X1，X2，X3代表测评要素；a1，a2，a3为各个测评要素的权重系数。

其中以各井区的裂缝发育程度为总体测评目标，以3种方法的预测成果为测评要素，以3个预测成果的准确程度为权重系数。为了满足数学模型的计算要求，需将定性分析结论进行量化以便定量计算，在预测成果中按裂缝发育程度分为好、中、差3类，分别赋予相应的权重，权重值越大，表示其裂缝发育程度越好。建立各预测方法的准确率与其影响因子之间的回归函数，从而计算出各预测方法的准确率，再将其值进行归一化处理后即得到权重系数值。曲率法预测准确率较低，权重系数值为15%；古构造应力场有限元数值模拟法预测和地震不连续性检测法预测的准确率较高，权重系数值分别为43%和42%。各种裂缝预测方法的测评要素值乘以其相应的权重系数，相加即得裂缝发育程度权重得分，得分越高，裂缝发育程度越好。计算结果如表1。

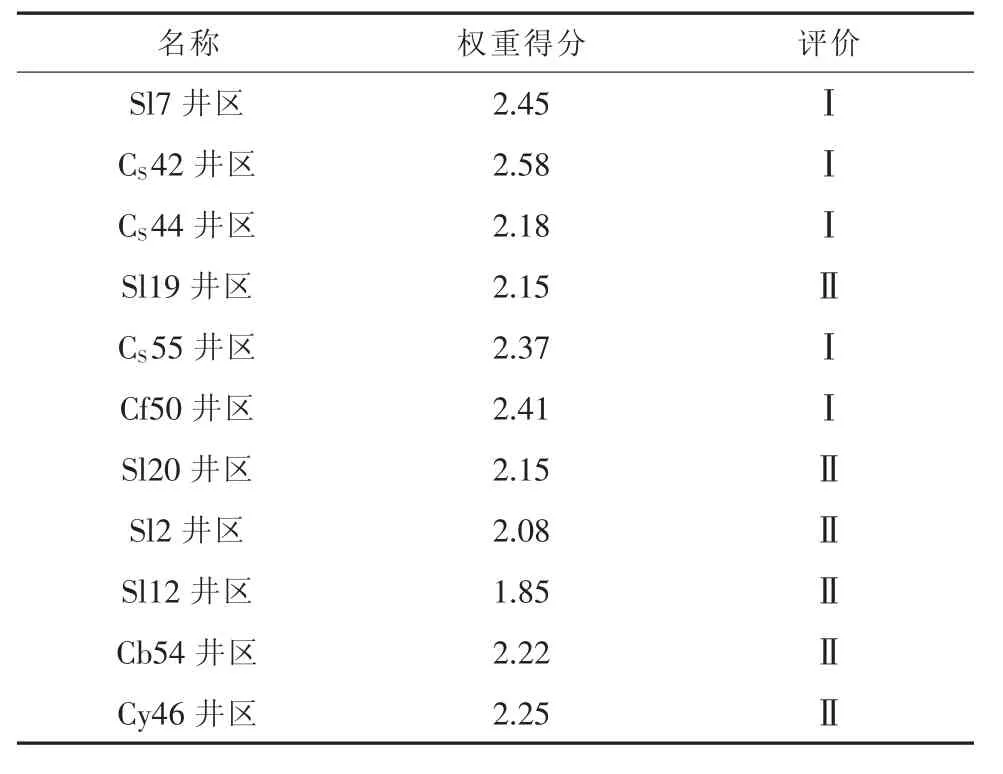
表1 裂缝发育程度权重评价表Table 1 Weight evaluation of fracture development

权重得分在2.3～3的区域为Ⅰ级裂缝发育区，这些区域其多种方法预测的结果相同，皆为裂缝发育程度高的区域，具有构造褶皱强、曲率高、邻近断层、破坏强度大、不连续性高等特点；权重得分在1.73～2.3的区域为Ⅱ级裂缝发育区，这些区域其多种方法预测结果不同，显示裂缝发育程度高或中等，具有构造褶皱强、曲率高、距断层近、破坏强度较小等特点（图 6）。

图6 千佛崖组裂缝综合预测图Fig.6 Synthetical fracture predication of Qianfoya Formation

4.2 预测效果分析

LZ地区主要经历了2次构造运动，构造运动的方式和强度比较容易确定，且有野外露头验证，构造分析的结果可靠性很高，这为构造应力场地质模型的建立提供了可靠的边界条件。因此，古构造应力场有限元模拟法和地震不连续性检测法的结果相对比较可靠，LZ地区构造主要为挤压型褶皱，易形成张性缝，用曲率法来预测张性缝是可行的。裂缝综合预测成果与目前掌握的钻井、测井和岩心资料基本相符（表2）。如裂缝发育区Sl10井千二段2 751～2 755.50 m放空0.25 m，说明地层中存在较大的缝、洞。

表2 千佛崖组裂缝发育情况统计表Table 2 Statistics of fracture developmentof Qianfoya Formation

5 结论

（1）LZ地区主要发育燕山期北西向平面“X”型剪切缝、喜山期北西向剖面“X”型剪切缝以及断裂的派生缝和伴生缝，其它类型裂缝发育程度较低。

（2）在裂缝构造成因分析的基础上，针对性地选用了构造曲率法、古构造应力场有限元模拟法与地震不连续性检测法，分别对裂缝进行了预测，再根据预测方法的准确率确定权重系数，将不同方法的预测成果进行综合权重计算，从而对LZ地区侏罗系千佛崖组致密储层的裂缝发育情况进行了综合预测，已钻井资料表明预测效果较好。

[1]Ameen M S，Buhidma I M，Rahim Z.The function of fractures and in-situ stresses in the Khuff reservoir performance，onshore fields，Saudi Arabia[J］.AAPG Bulletin，2010，94（1）：27-60.

[2]许同海.致密储层裂缝识别的测井方法及研究进展[J］.油气地质与采收率， 2005，12（3）：75-78.

[3]杨克明，张虹.地震三维三分量技术在致密砂岩裂缝预测中的应用[J］.石油与天然气地质，2008，29（5）：683-689.

[4]周新桂，邓宏文，操成杰.储层构造裂缝定量预测研究及评价技术[J］.地球学报，2003，24（2）：175-180.

[5]王国刚，苏培东，秦启荣.罗家寨构造嘉陵江组嘉四2段底部裂缝预测[J］.岩性油气藏，2009，21（4）：82-86.

[6]杨凯，郭肖.裂缝性低渗透油藏三维两相黑油数值模拟研究[J］.岩性油气藏，2009，21（3）：118-121

[7]王孟华，崔永谦，张锐峰，等.泥灰岩裂缝储层预测方法研究——以束鹿凹陷为例[J］.岩性油气藏，2007，19（3）：110-119.

[8]葛善良，周文，谢润成，等.复杂构造变形地区致密岩石力学性质实验分析[J］.岩性油气藏，2010，22（1）：59-64.

[9]Maerten L，Maerten F.Chronologic modeling of faulted and fractured reservoirs using geomechanically based restoration:Technique andindustryapplications[J］.AAPGBulletin，2006，90（8）：1201-1 226.

[10]陈波，田崇鲁.储层构造裂缝数值模拟技术的应用实例[J］.石油学报，1998，19（4）：50-54.

[11]李虎，秦启荣，王志萍，等.大邑构造须二段储层裂缝预测[J］.岩性油气藏，2010，22（2）：107-115.

[12]黄捍东，魏修成，叶连池，等.分形边缘检测在裂缝预测中的应用[J］.石油地球物理勘探，2002，37（1）：65-68.

[13]徐开礼，朱志澄.构造地质学[M］.北京：地质出版社，1998：111-118.

[14]童亨茂.储层裂缝综合预测方法在GBEIBE油田的应用[J］.中国石油勘探，2007，（3）：77-80.

[15]周艳辉，高静怀.局部结构熵算法在地震数据不连续性检测中的应用[J］.煤田地质与勘探，2007，35（1）：71-73.

Prediction method of fracture in tight sandstone reservoir and its application in LZ area

WANG Zhi-ping1， Qin Qi-rong1， SU Pei-dong1， FAN Xiao-li2
（1.School of Resources and Environment， Southwest Petroleum University， Chengdu 610500， China；2.Research Institute of Exploration and Development， Zhongyuan Oilfield Company， Sinopec， Puyang 457001， China）

The reservoir in LZ area is tight sandstone reservoir,and fractures control the reservoir spaces and well capacity.Based on the analysis of structural features and evolution,combined with the fracture divided period coordination on the basis of outcrop data,the tectonic origin of fractures is analyzed.It is considered that the fractures developed in the study area mainly are shear fracture,tensional fracture,associated and derived fractures with faults.The constructional curvature method,paleotectonic stress field finite element modeling method and seismic discontinuity detection method are applied to predict the different fractures respectively.The weight is adopted to evaluate the prediction results.It is to establish the regression function between the accuracy of the prediction method and its influencing factors,and then define the weight coefficient through the prediction accuracy and calculate the weights of the different prediction results.Finally it can be used to predict the fracture development in tight sandstone reservoir in the studyarea.The well drillingdata prove the good prediction effects.

synthetical fracture predication； constructional curvature method；paleotectonic stress field；seismic discontinuitydetection；Sichuan Basin

TE122.2+21

A

1673-8926（2011）03-0097-05

2011-01-17；

2011-02-20

国家科技重大专项（编号：2008ZX05001）资助。

王志萍，1981年生，女，西南石油大学在读博士研究生，研究方向主要为储层裂缝特征及预测研究。地址：（610500）四川省成都市西南石油大学研究生部博 09级。E-mail：wzp1209@163.com

杨琦）