网格资源共享策略的最优反应动态模型

李志洁，王存睿

（大连民族学院计算机科学与工程学院，辽宁大连 116600）

网格资源共享策略的最优反应动态模型

李志洁，王存睿

（大连民族学院计算机科学与工程学院，辽宁大连 116600）

围绕网格环境中用户的资源共享策略，应用进化博弈理论中的最优反应动态机制，建立了网格用户最优反应动态模型并结合算例对网格用户共享策略的发展变化趋势进行了分析。研究结果显示有限理性的网格用户不能实现网格资源的最大化共享，需要结合其特殊性对原有的资源管理模式进行改进，以适应网格的实际情况。

网格;进化博弈;最优反应动态

网格环境［1－4］中参与者需要共享彼此多余的资源，要让用户随心所欲地共享网格中的各种资源，还必须解决资源共享的不确定性问题。网格资源分配属于动态系统，系统状态随时在变化，这就迫使网格实体在不完全信息情况下做出共享决策，这样的决策必然带有博弈的成分，因而可以用博弈论的模型加以分析。博弈论中一个重要的分支—进化博弈论（Evolution Game Theory）［5－7］是受到生物进化理论的启发而发展起来的。进化博弈论假设博弈方按照生物或者社会的方式反复进行博弈，改善了传统博弈分析的多重均衡问题，因而可对群体行为的动态调整过程进行更为全面的分析，加强博弈分析的理论基础。进化博弈分析中模拟有限理性博弈方学习博弈和调整策略过程的一个典型机制就是最优反应动态。本文将利用最优反应动态机制深入研究网格资源共享问题，其目的不在于给出用户的最优策略选择，而在于从资源配置入手研究动态关系的优化，分析有限理性用户组成的网格群体的策略调整过程、趋势和稳定性，这样才有可能抓住导致网格资源管理复杂性的主要环节，打破制约网格技术迈向实用化的主要瓶颈。

1 最优反应动态

进化博弈理论强调系统达到均衡的动态调整过程，认为系统的均衡是达到均衡过程的函数，即均衡依赖于达到均衡的路径。一些学者曾提出了用于描述不同动态过程的动态机制。而本文所采用的是最优反应动态（Best－response Dynamics）机制［8］。所谓最优反应动态是指少数有快速学习能力的有限理性博弈方之间的重复博弈和策略进化。这种分析框架的理性假设为:博弈方具有相当快的学习能力，即使在复杂局面下准确判断分析和运用预见性的能力稍差，也能对不同策略的结果作出比较正确的事后评估，并进行相应的策略调整。因此已知给定的上一轮博弈结果，各个博弈方本次博弈都能找到针对前期博弈结果的最佳反应策略。最优反应动态假设博弈方虽然缺乏分析动态关系和预见能力，但是能够立即总结上一阶段的博弈结果，并相应的调整策略。这些博弈方的策略调整虽然针对上一期对手是正确的，但对当前的对手策略不一定正确，因为对手的策略也在调整，而这正体现出了博弈方的有限理性和缺乏预见的能力。在最优反应动态机制下，每个博弈方与对手反复进行博弈的过程中如果出现策略的收敛，即趋向一于个唯一的稳定状态，那么就得到最终的博弈均衡解，即进化稳定策略（Evolutionary Stable Strategy，ESS）。进化稳定策略意味着博弈方采用特定策略的比例达到该水平之后不再发生变化。此时最优反应动态就不再要求任何博弈方改变策略，这不仅是单个博弈方的策略稳定性，而且是群体意义上的策略稳定性。当群体中所有个体都选择进化稳定策略时群体所处的状态，就称为进化稳定状态，此时系统所达到的均衡称为进化稳定均衡。进化稳定策略ESS的定义如下［9］:设s是博弈G的一个策略组合，如果存在任意小的ε，对任意的s'≠s和ε∈（0，1］，满足

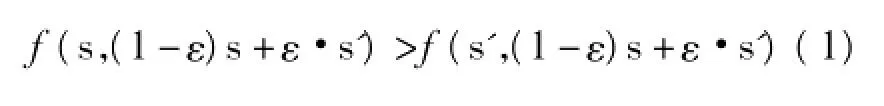
则称s是一个“进化稳定策略”。在上述不等式中，表达式f（策略1，策略2）表示博弈方在双方策略为（策略1，策略2）时的得益。在此定义中，ESS代表一个群体抵抗变异侵袭的一种稳定状态，当主导策略s受到少量（ε%）变异策略侵袭时，定义中的不等式要求主导策略严格优于变异策略。

2 网格资源共享问题的博弈框架

2.1 网格资源共享问题

网格计算通过利用大量异构计算机的未用资源，为解决大规模的计算问题提供了一个模型。这样，网格计算就形成了一个多用户环境。而资源管理往往假设网格用户都是完全理性的，在策略选择上不会犯错误。而网格的异构性、动态性和协同性使得网格参与者无法满足完全理性的要求，故以计算资源（CPU）为核心的资源共享存在以下难题:在资源共享过程中，每个参与的用户是有限理性的，这意味着参与者往往不能或不会采用完全理性条件下的最优策略，存在着对其他用户理性的信任问题，或者说在贡献本地资源的同时怀疑其他用户可能不共享资源。因此，资源共享具有不确定性，协调网格用户的共享策略是经常遇到的难题。本文采用进化博弈的理论方法研究网格用户的资源共享问题。在网格参与者策略选择的过程中，个体收益与群体其他成员的收益之间具有紧密联系。资源配置博弈的本质是动态的你得我失，未必均衡，但长期的博弈行为可能出现稳定的结果，形成各得其所的策略均衡。因此，建立基于进化博弈理论的网格资源配置模型，尤其是引入动态均衡概念，必将改善网格这种复杂系统的资源管理能力，获得有效的资源共享。

根据进化博弈模型的思想，本文所要解决的网格资源共享是一个研究网格用户的共享策略随时间变化的动态博弈系统，重点关注用户共享策略变化的筛选过程。该系统具有如下特点:①对称博弈，虽然网格用户在选择出价策略时要面其它所有用户，但总可以假设博弈是在成对的用户之间进行的;②策略调整，可供网格用户选择的有两种共享策略，一种是共享本地资源的策略，另一种是不共享本地资源的策略;③学习速度快，指的是网格用户虽然缺乏预见能力，但是能给立即对上一期博弈的结果进行总结并调整本期策略;④收益导向，网格用户在反复进行的博弈中，总会选择能够获得最大收益的策略。关于网络的拓扑图，本文做了如下假定。假设共有N个网格用户处于如图1所示的圆周上的N个位置，每个用户都与其左右邻居反复博弈。图中实线表示两个用户之间有网络连接，可以进行博弈，虚线表示期间有若干个用户。

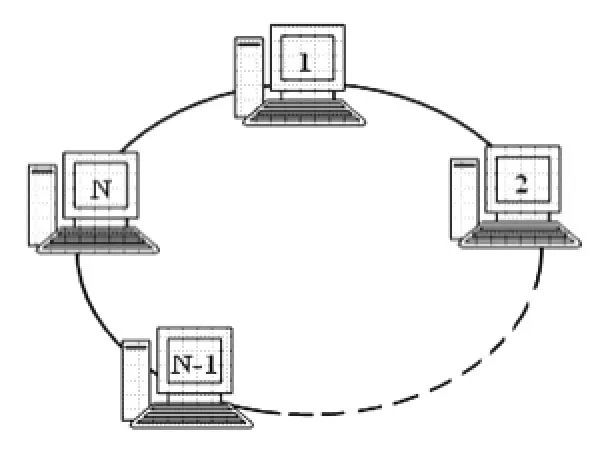
图1 网格用户的网络拓扑图

2.2 博弈框架

有限理性下的网格资源共享是一个需要不断学习的过程。进化博弈实际上就是有限理性个体组成的特定群体内成员间的反复博弈，来达到进化稳定均衡。要对网格资源共享博弈进行有限理性分析，必须先确定分析框架，包括理性层次和最优反应动态策略调整模式，以及博弈方群体的规模、分布和相互博弈方式。对于第一个方面，我们假设网格用户虽然缺乏分析交互动态关系和预见能力，但是能够立刻对上一阶段的博弈结果进行总结，并作出相应的策略调整，即每一次用户的调整都是针对其他用户的策略作出最优反应。对于第二个方面，我们假设共有N个网格用户分别处于圆周上的N个位置，每个用户都与其左右相邻的两个用户反复博弈如图1所示。既然每个用户都是有限理性的，那么在初次进行博弈时每个位置的用户都既可能采用不共享策略，也可能采用共享策略。因此，初次博弈总共有2N种可能的情况。下面对这些网格用户根据最优反应动态进行策略调整的规则作一些分析。

为了简化研究问题，先把博弈系统中进行共享博弈的网格用户群抽象为两个用户的群体，他们都是有限理性的博弈方，在出价博弈过程中，假定每个网格用户都面临两种策略选择，即共享策略和不共享策略，网格用户选择不同的策略所获得的得益水平由图1给出，由此构造一个随机配对的博弈框架，可用图2所示的2×2矩阵来表示。这种博弈的特征是两个博弈方在策略和得益方面都是对称的，因此，一个用户究竟是在网格用户1的位置博弈还是在网格用户2的位置博弈并没有区别。

图2 网格用户选择共享策略的得益矩阵

图2中A策略是不共享策略，B策略是共享策略。P1是网格用户均选择不共享策略时博弈双方所获得的得益水平，P4是网格用户均选择共享策略时博弈双方所获得的得益水平，P2是选择不共享策略的用户遇到选择共享策略的用户时所获得的得益水平，P3是选择共享策略的用户遇到选择不共享策略的用户时所获得的得益水平。在网格资源共享过程中，如果博弈双方都采用相同的策略，那么他们获得的得益水平是一样的，都为P1或P4，而且P4＞P1。而如果博弈双方采用不同得策略，则不共享资源的网格用户必然侵占了选择共享策略用户的部分资源份额，因此不共享资源的用户所获得的得益必然大于共享资源用户的得益，即P2＞P3。通过纳什均衡分析可以确定该博弈有两个纯策略纳什均衡（A，A）和（B，B），后者明显优于前者。如果用户是完全理性的，那么博弈结果应该是（B，B）。但是在有限理性的制约下，网格用户事先并不知道哪种策略最好，经过反复博弈，采用共享策略的用户可能转向不共享策略，转向不共享策略的用户也可能回到共享策略，这导致无法预测这个博弈的结果。下面对求解该博弈的进化稳定均衡进行分析。

令xi（t）为在t时期用户i的邻居中采用A策略邻居的数量，该数量最多为2个。故第t期如果用户i采用A策略，那么得益为xi（t）·P1+［2－xi（t）］·P2;如果用户i采用B策略，那么得益为xi（t）·P3+［2－xi（t）］·P4。下面我们分三种情况对第t+1期的用户策略进行讨论。

①如果xi（t）·P1+［2－xi（t）］·P2＞xi（t） ·P3+［2－xi（t）］·P4，那么第t期用户i采用A策略的得益大于采用B策略的得益，即xi（t）＞2 （P4－P2）/（P1－P2－P3+P4）时，用户i在第t+1期会采用A策略。

②如果xi（t）·P1+［2－xi（t）］·P2＜xi（t） ·P3+［2－xi（t）］·P4，那么第t期用户i采用B策略的得益大于采用A策略的得益，即xi（t）＜2 （P4－P2）/（P1－P2－P3+P4）时，用户i在第t+1期会采用B策略。

③如果xi（t）·P1+［2－xi（t）］·P2=xi（t） ·P3+［2－xi（t）］·P4，那么第t期用户i采用A策略的得益等于采用B策略的得益，即xi（t）=2 （P4－P2）/（P1－P2－P3+P4）时，用户i在第t+1期会采用与第t期同样策略。

根据以上分析，网格用户的最优反应动态方程可以表示如下:

其中，Strategy（t）表示第t期用户i采用的策略，w为临界值2（P4－P2）/（P1－P2－P3+P4），由上述三种情况分析得出。式（2）表明，当网格用户采取A策略的得益大于采取B策略的得益时，在下一期网格用户都能作出最优反应，即都采取A策略;反之，则在下一期网格用户都将采取B策略。当二者相当时，采取A策略的用户个数保持不变。

3 算例分析

3.1 进化算法

根据最优反应动态机制，用户根据上期博弈的结果确定本期博弈的共享策略。初次博弈时，N个用户的共享策略随机指定，可为共享策略和不共享策略。每个用户分别与其左右邻居进行反复博弈。按照编号有序的原则，如果当前为用户i，则下一个用户的编号为（i mod N）+1，而前一个用户的编号为（（（i mod N）+N－1）mod N）+1。本文进化博弈中用户共享策略选择的最优反应动态算法可以描述为:

①博弈开始时，初始化用户数量N及得益矩阵P1，P2，P3，P4;

②随机指定用户的初始策略，并计算临界值w;

③for每个用户i do

统计邻居中采用A策略的用户数量k;

if k＞w then

用户下一期采用A策略;

else if k＜w then

用户下一期采用B策略;

else

用户下一期采用与本期相同的策略;

④if本期博弈结果与上期结果相同then

转步骤⑤;

else

返回步骤③;

⑤算法结束.

3.2 实验结果

为了对最优反应动态算法的博弈过程和结果进行分析，下面通过一个典型的算例，对算法执行过程中用户策略的动态调整和稳定结果做进一步的讨论。设网格系统中有16个有限理性的用户，他们具有相同的得益矩阵如图3所示，且只有共享和不共享两种策略可以选择。

图3 网格用户博弈的得益矩阵

N个用户的初始策略随机指定为s1=B，s2= B，s3=B，s4=B，s5=B，s6=B，s7=A，s8=B，s9= B，s10=A，s11=A，s12=B，s13=B，s14=B，s15=B，s16=A。根据得益矩阵，可计算临界值w=0.667。为了直观的表示用户的初始策略，本文绘制了对应的饼图如图4所示。图4中共有16个扇区分别表示16个用户的策略，其中分离出来的扇区表示该用户选择的是不共享策略，而没有分离的扇区则表示选择的是共享策略。

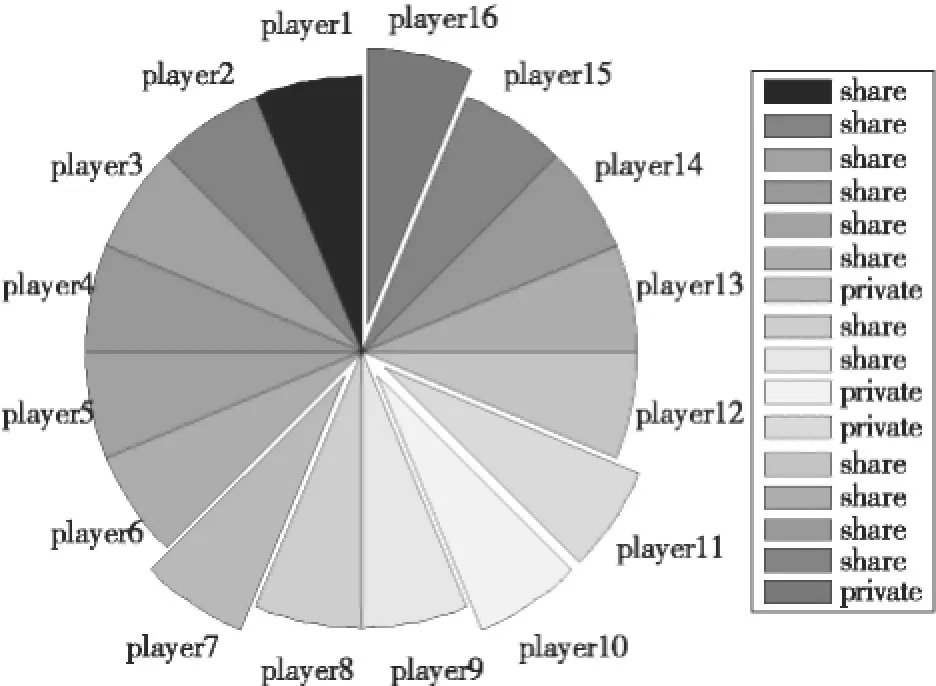
图4 网格用户初始策略饼图

表1和表2给出了网格用户的进化博弈过程。从下面两个表中的结果可以看出，进化博弈一共进行了8个时期，从最初个别用户的扇区分离进化到所有用户的扇区分离，由于第9期与第8期的结果一样，所以算法结束。前面我们已经假定了网格用户是具有快速学习能力的有限理性群体，故进化博弈的收敛速度很快。根据最优反应动态机制，每期用户都会针对上一期的博弈结果而调整共享策略，以达到最大化自己得益的目的。经过反复的策略调整，最终所有用户都收敛到了采用不共享策略的稳定状态，此时最优反应动态不再要求任何用户改变策略，这个不仅仅是单个用户的策略稳定性，而且是群体意义上的策略稳定性。这个算例只是众多例子中的一个，但是其折射出有限理性用户在资源共享过程中的一个趋势，即不共享自己的资源。即使都采用共享策略的得益大于不共享策略，受到理性层次的制约，网格用户仍然会收敛到不共享的稳定状态，这也正是有限理性和完全理性的区别所在。虽然网格的最初目的是共享所有参与者的资源，提高资源利用率，但现实情况恰恰相反，如果没有很好的激励机制来维护网格系统，最终的结果必然是没有用户愿意贡献自己的资源。

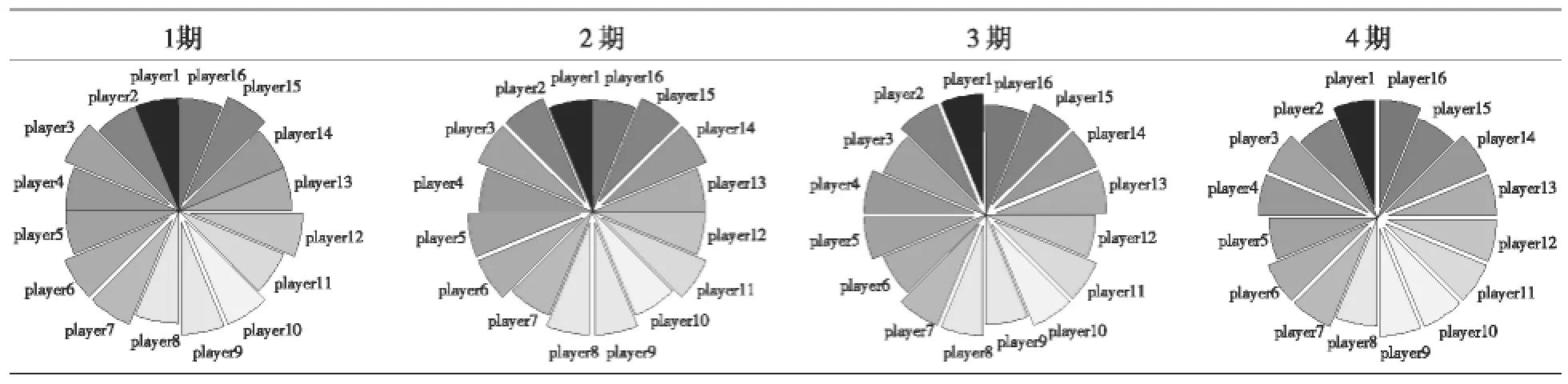
表1 第1期至第4期的网格用户进化博弈过程

表2 第5期至第8期的网格用户进化博弈过程

4 结论

在博弈框架下研究网格用户共享策略的动态演化过程，从网格参与者的角度，深入研究有限理性网格用户策略调整的过程和动态稳定性之间的关系，研究内容可为网格实际应用中资源配置进化博弈的定量表达提供理论依据。目前网格用户的资源共享过程非常适合使用最优反应动态机制来分析。通过模拟实验表明，所有用户都采取不共享策略是系统的最容易出现的稳定状态。这与网格的共享精神是相背离的。所以，网格用户受到理性层次的制约，并不能很好的发挥提高资源利用率的作用。为此，需要向网格系统注入合适的激励机制以维护系统的良好运行。如何在多用户的动态环境中协调资源的共享使用，实现资源的优化配置，这样的激励机制的方法与规则是有待深入研究的问题。

［1］FOSTER I，KESSELMAN C，TUECKE S.The anatomy of the grid:Enabling scalable virtual organizations［J］.International Journal of Supercomputer Applications，2001，15（3）:200－222.

［2］YANG Guangwen，JIN Hai，LI Minglu，et al.Grid computing in China［J］.Journal of Grid Computing，2004，2（2）:193－206.

［3］FOX G.Grid computing environments［J］.IEEE Computational Science and Engineering，2003，5（2）:68－72.

［4］KRAUTER K，BUYYA R，MAHESWARAN M.A Taxonomy and Survey of Grid Resource Management System for Distributed Computing［J］.Software:Practice and Experience，2002，32（2）:135－164.

［5］FATIMA S S，WOOLDRIDGE M，JENNINGS N R.A comparative study of game theoretic and evolutionary models of bargaining for software agents［J］.Artificial Intelligence Review，2005，23（2）:185－203.

［6］ANTAL T，SCHEURING I.Fixation of strategies for an evolutionary game in finite populations［J］.Bulletin of Mathematical Biology，2006，68（8）:1923－1944.

［7］ALTMAN E，BARMAN D，EL AZOUZI R，et al.Pricing differentiated services:A game－theoretic approach［J］.Computer Networks，2006，50（7）:982－1002.

［8］谢识予.经济博弈论［M］.2版.上海:复旦大学出版社，2002.

［9］王鑫，李研.区域电力市场中发电商竞价策略的最优反应动态模型［J］.华北电力大学学报，2006，33 （6）:51－54.

Best－response Dynamic Model for Resource Sharing Strategy in Grid

LI Zhi－jie，WANG Cun－rui
（School of Computer Science＆Engineering，Dalian Nationalities University，Dalian Liaoning 116605，China）

Concerning the resource sharing strategy of grid user，the dynamics model of rational user based on the best－response dynamic mechanism has been established.With typical case，the evolution trend of user sharing strategy has been analyzed.The result showed that the maximize sharing of grid resources cannot be achieved because of the bounded rationality of grid user.Thus，the original resource management should be improved to adapt to the actual situation of grid environment.

Grid;evolutionary game;best－response dynamics

TP393

A

1009－315X（2011）03－0291－05

2011－03－23

中央高校基本科研业务费专项资金资助（DC10040110）;辽宁省教育厅科学技术研究项目支持（2010044）;大连民族学院博士启动基金项目支持（20086205）。

李志洁（1978－），女，黑龙江鸡西人，副教授，博士，主要从事智能算法研究。

（责任编辑 刘敏）