双扩张Schrödinger-Virasoro代数的导子代数与自同构群
2011-01-12徐崇斌
徐崇斌
(温州大学数学与信息科学学院,浙江温州 325035)
双扩张Schrödinger-Virasoro代数的导子代数与自同构群
徐崇斌
(温州大学数学与信息科学学院,浙江温州 325035)
双扩张Schrödinger-Virasoro代数是扩张Schrödinger-Virasoro代数的自然推广.充分讨论了双扩张Schrödinger-Virasoro代数的导子代数与自同构群,讨论结果适用于任意有限秩情形.
双扩张Schrödinger-Virasoro代数;导子代数;自同构群
1 预备知识


2 双扩张Schrödinger-Virasoro代数的导子代数




3 双扩张Schrödinger-Virasoro代数的自同构群

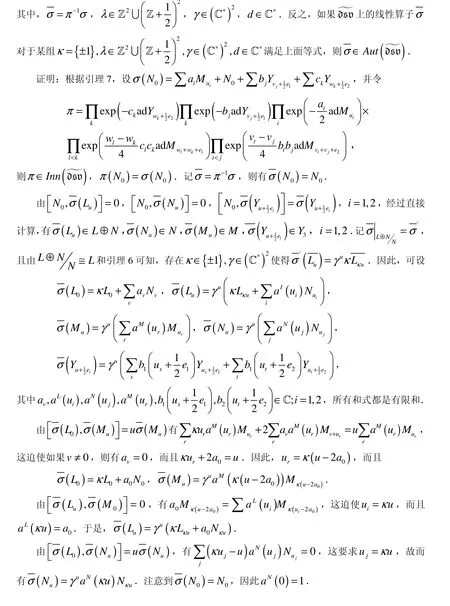


[1] Roger C, Unterberger J. The Schrödinger-Virasoro Lie group ane algebra:from geometry to representation thery [J]. Ann Henri Poincare, 2006, 7: 1477-1529.
[2] Unterberger J. On vertex algebra representations of the Schrödinger-Virasoro Lie algebra [J]. Nuclear Physics B, 2009, 823(3): 320-371.
[3] Gao S, Jiang C, Pei Y. Structure of the extended Schrödinger-Virasoro Lie algebra [J]. Alg Colluq, 2009, 16(4): 549-566.
[4] Tan S, Zhang X. Automorphisms and Verma modules for generalized Schrödinger-Virasoro algebras [J]. J Alg, 2009, 322: 1379-1394.
[5] Farnsteiner R. Derivations and extensions of fnitely generated graded Lie algebras [J]. J Alg, 1988, 118(1): 34-45.
[6] Dokovic D Z, Zhao K. Derivations, Isomorphisms and second cohomology of generalized Witt algebras [J]. Tran Amer Math Soc, 1998, 350: 643-664.
Study on Derivation Algebra and Automorphism Group of Double Extended Schrödinger-Virasoro Algebra
XU Chongbin
(School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)
Double extended Schrödinger-Virasoro algebra is a natural generalization of extended Schrödinger-Virasoro algebra. In this paper, its derivation algebra and automorphism group were discussed. The achievement of the discussion is applicable to any finite rank.
Double Extended Schrödinger-Virasoro Algebra; Derivation Algebra; Automorphism Group
(编辑:王一芳)
O152.5
A
1674-3563(2011)06-0001-08
10.3875/j.issn.1674-3563.2011.06.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得
2011-02-21
徐崇斌(1977- ),男,湖北黄梅人,讲师,硕士,研究方向:代数
