＊ 带Poisson跳和M arkovian调制的年龄相关随机种群方程数值解的收敛性

马维军,张启敏

(宁夏大学数学计算机学院,宁夏银川 750021)

＊带Poisson跳和M arkovian调制的年龄相关随机种群方程数值解的收敛性

马维军,张启敏

(宁夏大学数学计算机学院,宁夏银川 750021)

研究了带Poisson跳和Markovian调制的年龄相关随机种群方程数值解的收敛性,在给定条件下证明了数值解收敛到解析解,并给出了Euler逼近的阶数.

与年龄相关随机种群方程;Markovian调制;Poisson跳;数值解;收敛性

0 引言

考虑如下与年龄相关的随机种群系统:

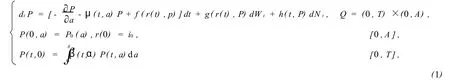
近年来,很多学者更加关注随机微分方程数值解的研究.例如,Wang讨论了带Poisson跳和Markovian调制的随机时滞微分方程数值解的收敛性[1],Svishchuk和 Kazmerchuk研究了带Poisson跳和Markovian调制的随机时滞微分方程的指数稳定性[2].Luo给出了带Poisson跳和M arkovian调制的It^o随机时滞微分方程的比较原则和指数稳定性[3].然而对与年龄相关的随机种群方程,当h=0时,Zhang证明了系统(1)强解的存在性、唯一性,指数稳定性和数值分析[4-5],Gu讨论了与年龄相关的具有扩散的随机种群系统数值解的收敛性[6],Li研究了与年龄相关的随机种群方程数值解的收敛性[7].

一般情况下,形如(1)的种群方程的解析解很难求得,故通常利用数值方法求得其数值逼近解,因而研究种群系统数值解的收敛性问题具有重大意义.而目前关于带Poisson跳和Markovian调制的年龄相关随机种群系统数值解的收敛性研究很少见到.本文研究了方程(1)数值解的收敛性,并给出数值解收敛的阶数,所得到的结论是文献[7-9]的扩展.

1 预备知识

设(Ω,F,{Ft}t≥0,P)是一完备概率空间,{Ft}t≥0是其上的一个滤子且满足一般性条件(即左极限右连续的,且F0包含所有的零测集).

设N(t)是强度为λ的数值 Poisson过程,假设N(t)与Brow n运动W t相互独立.设{r(t),t≥0}是定义在概率空间(Ω,F,P)上取值于有限状态S={1,2,…,N}的右连续Markov链,其生成元Γ=(γij)N×N如下给定:

其中Δ＞0.若i≠j,γij≥0表示从状态i转移到状态j的概率,γii=- ∑i≠jγij.假设r(·)与Brow n运动W t和Poisson过程N(t)相互独立.易知,r(t)的每一个样本轨道是右连续的阶梯函数,且在R+上的任何一个有限子区间上至多含有限多个跳跃点.

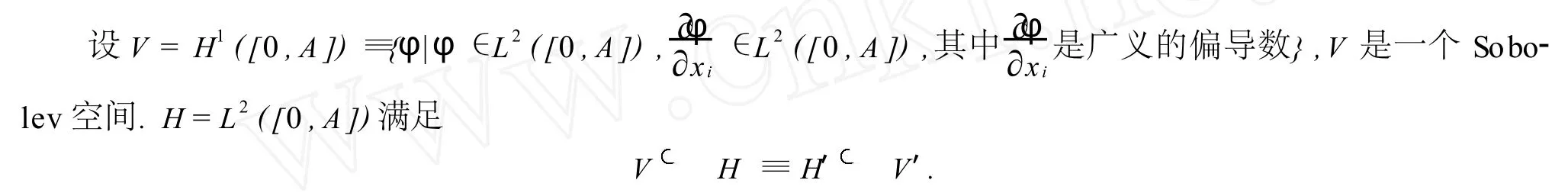
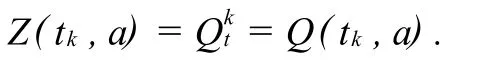
我们假设满足以下条件:

2 引理

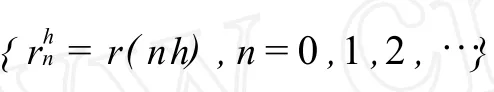
P(h)=(Pij(h))N×N=ehΓ.

引理2.2 若条件(ii)-(iii)成立,则存在常数k≥2,C1＞0使得

证明 对|Pt|k应用 It^o公式,可得

3 主要结果

定理3.1 若条件(i)-(iii)成立,则

[1] Wang La-sheng,Xue Hong.Convergence of Numerical Solutions to Stochastic Differential Delay Equations with Poisson Jump and Markovian Switching[J].A pp lied Mathematics and Computation,2007,188:1161-1172.

[2] Svishchuk A V,Kazmerchuk Yu I.Stability of Stochastic Delay Equations of Ito form with Jumps and Markovian Switchings,and their Applications in Finance[J].Theor Probab Math Stat,2002,64:167-178.

[3] Luo J.Comparison Principle and Stability of Ito Stochastic Differential Delay Equations with Poisson Jump and Markovian Switching[J].Nonlinear Anal,2006,64:253-262.

[4] Zhang Q M,Liu W A,Nie Z K.Existence,Uniqueness and Exponential Stability for Stochastic Age-dependent Population[J].Applied Mathematics and Computation,2004,154:183-201.

[5] Zhang Q M,Han C Z.Numerical Analysis for Stochastic Age-dependent Population Equations[J].Applied Mathematics and Computation,2005,169:278-294.

[6] Gu Xiao-jun,Zhang Qi-min.Convergence of Numerical Solutions to Stochastic Age-structrued Population System with Diffusion[J].宁夏大学学报:自然科学版,2008,29(3):198-202.

[7] Li Rong-hua,Meng Hong-bing,Chang Qin.Convergence of Numerical Solutions to Stochastic Age-dependent Population Equations[J].J Com put Appl Math,2006,193:109-120.

[8] Zhou Shao-bo,Wu Fu-ke.Convergence of Numerical Solutions to Neutral Stochastic Delay Differential Equations with Markovian Switching[J].Computational and A p p lied Mathematics,2009,229:85-96.

[9] Mao Xue-rong,Sabanis S.Numerical Solutions of Stochastic Differential Delay Equations Under Local Lipschitz Condition[J].J Com put Appl Math,2003,151:215-227.

Convergence of Numerical Solutions to Stochastic Age-dependent Population Equations with Poisson Jumps and Markovian Switching

MA Wei-jun,ZHANG Qi-min
(School of Mathematics and Computer Science,Ningxia University,Yinchuan750021,China)

The convergence of numerical approximation of stochastic age-dependent population equations with Poisson jumps and Markovian switching is studied.It is proved that the numerical approximation solutions converge to the analytic solutions of the equations under the given conditions.The order of the Euler approximation is also provided.

stochastic age-dependent population equations;Markovian switching;Poisson jump s;numerical solutions;convergence

O211.63

A

0253-2395(2011)01-0051-09＊

2010-04-18;

2010-08-17

国家自然科学基金(11061024)

马维军(1981-),男,宁夏人,硕士,从事随机计算及其应用的研究.E-mail:maweijun_2008@163.com