磁异常相关的四种物理信号性质分析

王 磊,卞光浪,翟国君,欧阳永忠,陆秀平,吴太旗,任来平

（1.91550部队,辽宁 大连116023;2.海军大连舰艇学院 海测工程系,辽宁 大连116018;3.海军海洋测绘研究所,天津 300061）

磁异常相关的四种物理信号性质分析

王 磊1,卞光浪2,3,翟国君3,欧阳永忠3,陆秀平3,吴太旗3,任来平3

（1.91550部队,辽宁 大连116023;2.海军大连舰艇学院 海测工程系,辽宁 大连116018;3.海军海洋测绘研究所,天津 300061）

建立了一种特殊坐标系，从理论上推导了磁异常强度、全梯度模信号、张量梯度模信号和拉普拉斯信号等物理信号的表达式，并分析了它们具有的物理性质。采用仿真计算表明：拉普拉斯信号在空间的等值面非常接近于球面，其在平面上的等值线极大值对应磁性目标中心位置，而其它3种信号在平面上等值线极大值与磁性目标中心位置则存在一定的偏差。而且，4种物理信号随测点至磁性目标中心间距离的衰减速度也存在差异，其中，拉普拉斯信号与距离呈5次方衰减，磁异常强度与距离呈3次方衰减，而全梯度模信号和张量梯度模信号与距离都成4次方衰减。

磁性目标；磁异常强度；全梯度模信号；张量梯度模信号；拉普拉斯信号

磁测方法是推断地球地质结构以及勘查油气与矿产资源分布状况的重要手段[1]。近年来，在开发利用海洋的过程中，磁探测技术在水下磁性目标探测方面也得到越来越广泛的应用[2]。在磁性目标探测数据处理时，经常需要将磁场观测数据转化为某些特殊物理信号，如磁异常强度、总梯度模信号（解析信号）、张量梯度模信号和拉普拉斯信号等，据此推断磁性目标的平面或空间位置，为此，本文对这些物理信号所具有的物理性质进行分析，为定量或定性判断磁性目标属性提供理论依据。黄临平[3]和管志宁[4]等对总梯度模信号与磁化强度方向间关系从理论上进行了初步分析，认为总梯度模极大值处对应磁性目标中心或边缘，并通过仿真和实测数据对结论进行了验证。上述文献在理论推导过程中，为了推导出简洁的表达式，设定了诸多假设条件，导致方法不具备普遍性。在上述研究的基础上，根据上述物理信号具有旋转不变性[5]的特点，通过建立一种特殊坐标系，从理论上推导了拉普拉斯信号、磁异常强度、总梯度模和张量梯度模等信号的表达式，同时还分析了它们的物理性质。

1 物理信号表达式

自然界中一些有限大小的三度磁性体，当其中心埋深大于磁性体走向长度2～3倍时，它们在地表产生的磁场特征与磁偶极子磁场类似，因而将磁偶极子磁场模型作为研究对象同时具有理论意义和现实意义，国内外大多数磁性体定位方面研究成果[6-7]也是基于该磁场模型，本文的研究同样采用该磁场模型。

在右手笛卡尔坐标系中，设磁偶极子的中心位置为（x0，y0，z0），矢量磁矩为 m=mxi+myj+mzk，磁偶极子中心至测点（x，y，z）矢径为 r=rxi+ryj+rzk。以 Bx、By和 Bz表示磁偶极子引起的磁异常强度BT在x方向、y方向与z方向磁场分量，有如下各式成立[8]：

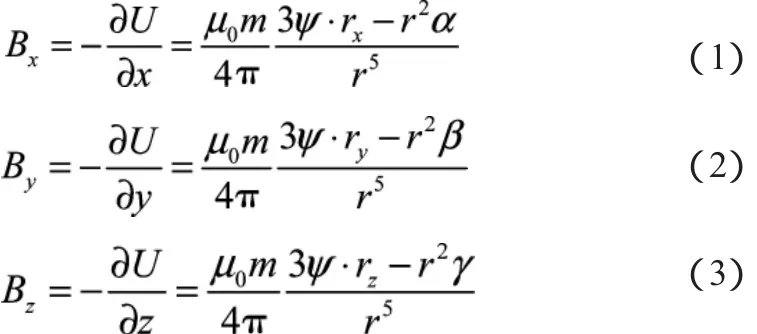
式中：μ0=4π×10-7；rx=x-x0；ry=y-y0；rz=z-z0；r=|r|；ψ=αrx+βry+γrz；α=cosIcosA；β=cosIsinA；γ=sinI；I与 A 分别为磁化强度倾角及x轴剖面与磁化强度水平投影夹角，U为磁偶极子产生的磁位，m=||m||为磁矩模。

磁异常强度BT可用Bx、By和Bz的均方根形式表示为：

对BT进行拉普拉斯算子运算得：

式中：

（5）式中Bij（i，j=x,y,z）表示Bi分量在j方向的偏导数，其通式为：

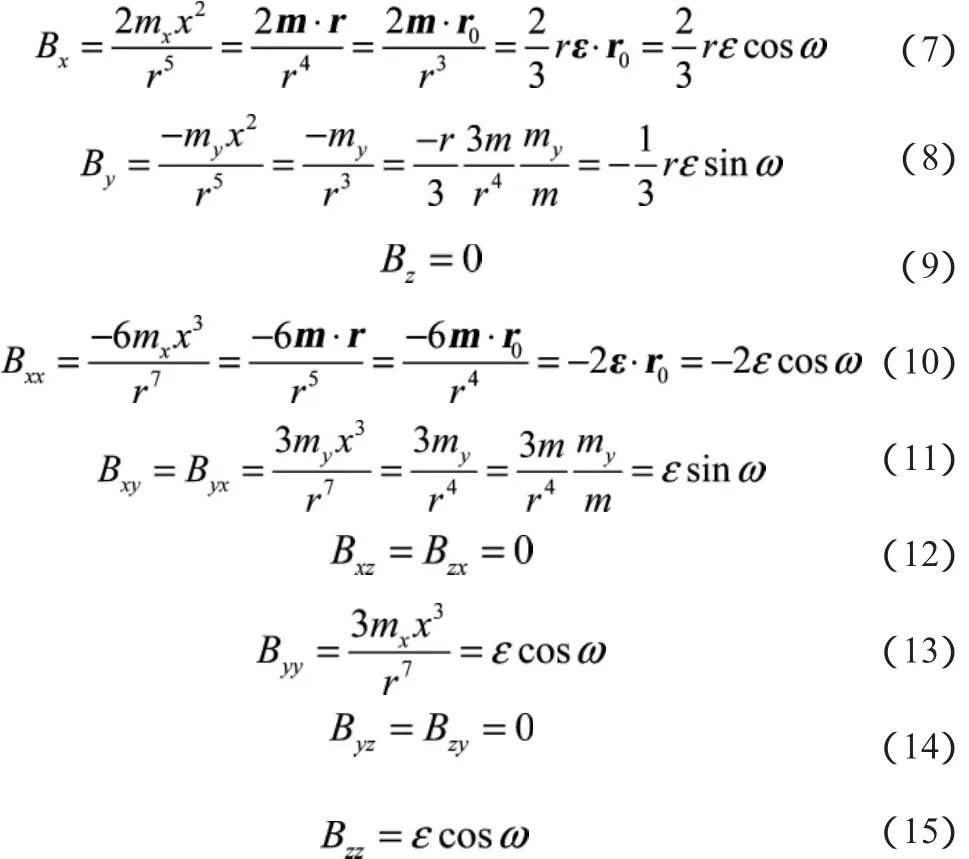
将（7）式～（15）式代入（5）式，整理后得：

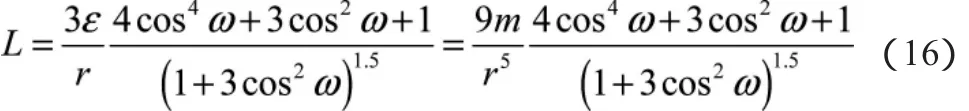
（16）式即为磁异常强度拉普拉斯信号L表达式，可见，L与磁偶极子磁矩m、磁偶极子中心至测点距离r以及两者之间夹角ω有关。

限于篇幅，不加证明地给出该坐标系下磁异常强度BT、张量梯度模C以及地磁场方向与磁化强度方向相同时总梯度模信号AAS表达式分别为：

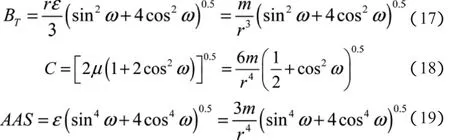
从（16）式～（19）式可以看出，各物理信号随测点至磁性目标中心间距离的衰减速度并不一致，其中，磁异常强度衰减速度最慢，大致呈3次方衰减；拉普拉斯信号衰减速度最快，呈5次方衰减；张量梯度模和总梯度模信号衰减速度相同，呈4次方衰减。以下将分别分析各种信号与磁化强度方向间关系。

2 物理信号性质

根据（16）式 ～（19）式有：

上述各式中，

当固定 m，BT，AAS，C 和 L 时，（20）式 ～（23）式就是 4 种物理信号等值面上测点与磁偶极子中心距离，可见，等值面的形状与fk（ω）有关，如果fk（ω）=1（k=BT,AAS，C，L），表明相应信号的等值面为球面。图1为ω∈[0°，90°]时fk（ω）（k=BT,AAS，C，L）随 ω 的变化规律。

从图1中可以看出，fL（ω）取值始终在1附近，表明拉普拉斯信号的等值面非常接近于球面，换言之，磁化强度方向取任意值，拉普拉斯信号在平面上的等值线接近于圆形，观测平面上的拉普拉斯信号的极大值位置始终对应磁性目标中心位置。而（ω）最大值超过1.25，最小值为1，表明当且仅当观测平面垂直于磁化强度方向时，其磁异常强度的极大值才对应磁性目标中心位置；当观测平面与磁化强度方向不垂直时，磁异常强度的极大值总是偏离磁性目标的中心位置，且观测平面的法线方向与磁化强度方向夹角（取锐角）越大，两者偏差也越大。总梯度模信号与张量梯度模信号变化幅值要小于磁异常强度信号变化幅值，因此，两信号极大值偏离磁性目标中心的幅度要小于磁异常强度极大值偏离磁性目标中心的幅度。可以看出，除拉普拉斯信号在空间的等值面为准球面外，其它3种信号在空间的等值面均非球面，对应地，3种信号在平面上的等值线也并非圆形。

图1 fk（ω）（k=BT,AAS，C，L）随 ω 变化关系

4种信号的f（kω）[ω∈[0°，90°]]最大值与最小值统计情况如表1所示。

表1中列出了各种物理信号f（kω）在 ω∈[0°，90°]区间内的极大值与极小值，两者的比值直接表明了信号空间等值面接近球面的程度，从而也反映信号在平面上的极大值与磁性目标中心的对应情况。经统计，f（Lω）极大值与极小值的比值最小，仅为 1.030 0：1（ω）极大值与极小值的比值最大，为1.259 9：1；fAAS（ω）极大值与极小值的比值为1.222 8：1；fC（ω）极大值与极小值的比值1.147 2：1。

表1 BT，AAS，C和L极大值与极小值统计情况

为了验证上述结论，同时更加直观地反映出各种信号在平面上的极大值与磁性目标中心位置的对应关系，下面用仿真球体磁异常数据进行分析。设地磁场倾角和偏角分别为I0＝70°与 A0＝10°，仿真的测区面积为 20 m×20 m，测线和测点间距均为0.5 m，球体的空间位置为(10 m，10 m，3 m)，其磁矩为10 Am2，磁化强度方向为I0＝40°与A0＝1°。采用球体磁场表达式仿真得到其在平面上总强度磁异常Bm、磁异常强度BT、总梯度模信号、张量梯度模信号和拉普拉斯信号的等值线如图2所示，图中，“+”为球体中心平面位置。

图2 信号在平面上的等值线图

从图2可以再次验证两个结论：第一，相比较其它几种信号而言，拉普拉斯信号极大值位置最接近球体中心平面位置，且其平面上的等值线非常接近于圆形，其它几种信号的极大值位置与球体中心位置均存在不同程度的偏离，其中，磁异常强度信号偏离程度最大。第二，(b)～(e)四种信号中相同数值的等值线宽度反映了信号随距离的衰减速度，信号衰减速度越快，其宽度越窄；反之，则越宽。以信号强度数值是5为例，拉普拉斯信号（与距离呈5次方衰减）宽度最窄，磁异常强度信号（与距离呈3次方衰减）宽度最宽，总梯度模信号和张量梯度模信号（均与距离呈4次方衰减）宽度则大体相当。可以根据上述结论，一方面，通过将观测得到的磁场数据转换为各种不同的信号，以此来判断磁性目标的位置；另一方面，利用拉普拉斯信号或张量梯度模信号的物理特性，设计磁性目标实时定位与识别系统。

3 结论

通过建立一种特殊坐标系，理论上推导了磁异常信号、总梯度模信号、张量梯度模信号以及拉普拉斯信号的表达式，研究表明：

（1）4种信号随测点至目标中心间距离衰减程度不同，拉普拉斯信号衰减最快，与距离呈5次方衰减；磁异常强度信号衰减最慢，与距离呈3次方衰减；全梯度模信号与张量梯度模信号衰减速度相同，均为4次方衰减。

（2）拉普拉斯信号的大小主要取决于观测点至目标中心间距离，受磁化强度方向的影响极小，因此，观测平面上拉普拉斯信号的极大值对应磁性目标中心的位置；而传统上认为总梯度模信号的极值位置对应磁性目标的中心位置这一说法并不完全准确，当且仅当观测平面垂直于磁化强度方向时，两者才相互对应。同时，磁异常强度和张量梯度模信号的极大值位置与磁性目标中心位置也存在一定的偏差。

（3）根据结论（1）和（2），在利用多传感器探测磁性目标中，可分步来定位与识别磁性目标。当探测载体距离磁性目标较远时，将磁场观测数据转换为磁异常强度信号，大体判断磁性目标位置，同时利用推进装置使探测平台靠近磁性目标，再进一步将磁场观测数据转换成拉普拉斯信号或张量梯度模信号，以精确确定磁性目标的位置。

[1]杨文采,余长青.根据地球物理资料分析大别—苏鲁超高压变质带演化的运动学和动力学[J].地球物理学报,2001,44(3)：346-359.

[2]Dwain K,Butler.Implications ofmagnetic backgrounds for unexploded ordnance detection[J].Journal ofApplied Geophysics,2003,54：111-125.

[3]黄临平,管志宁.利用磁异常总梯度模确定磁源边界位置[J].华东地质学院学报,1998,21(2)：143-150.

[4]管志宁,姚长利.倾斜板体磁异常总梯度模反演方法[J].地球科学-中国地质大学学报,1997,22(1)：81-85.

[5]Schmidt P W,Clark DA.The magnetic gradient tensor：Its properties and uses in source characterization[J].The LeadingEdge,2006,25,(1)：75-78.

[6]Sun K,O’Neill K,Shubitidze F,et al.Fast data-derived fundamental spheroidal excitation models with application toUXO discrimination[J].Transactions on EvolutionaryComputation,2005,43：2573-2583.

[7]GinzburgB,Frumkis L,Kaplan BZ.An efficient method for processingscalar magnetic gradiometer signals[J].Sensors and Actuators,2004,114：73-79.

[8]Gerovska D,Marcos J,StavrevP.Determination ofthe Parameters ofCompact Ferro-metallic Objects with Transforms ofMagnitude Magnetic Anomalies[J].Journal ofApplied Geophysics,2004,33：173-186.

[9]Wiegert R F.Magnetic anomalysensingsystemfor detection,localization and classification ofmagnetic objects：US，US6841994B1[P].2005-1-11.

Properties Analysis of Four Physical Signal Translated from Magnetic Anomaly

WANG Lei1,BIAN Guang-lang2,3,ZHAI Guo-jun3,OUYANG Yong-zhong3,LU Xiu-ping3,WU Tai-qi3,REN Lai-ping3
(1.91550 Troops,Dalian Liaoning 116023,China;2.Department of Hydrography and Cartography,Dalian Naval Academy,Dalian Liaoning 116018,China;3.Naval Institute of Hydrographic Surveying and Charting,Tianjin 300061,China)

A particular coordinate system is established.Then the expression of magnetic anomaly (MA)intensity,total gradient modules of magnetic anomalies(MATGM),total gradient contraction of the magnetic gradient tensor(MGTTGC)and Laplace signal(LS)are deduced theoretically,together with their physical properties analyzed.Adopting numerical calculation,the result indicates that the equiscalar of LS is very close to spherical surface in 3D space;accordingly,the maximum value of isoline is corresponding to magnetic object central position.However,the maximum value of other three signals’isolines has certain discrepancy with their central position.Moreover,the falloff rate of four signals with the distance between survey point and object center are different,that is,Laplace signal magnitudes that are associated with magnetic objects are proportional to 1/r5where “r” is the distance between the sensor and the magnetic object,and MA fields decrease with the inverse cube of distance to the objects.The falloff rate of MATGM is same as MGTTGC,which is proportional to 1/r4.

magnetic object;magnetic anomaly intensity;total gradient modules of magnetic anomalies;total gradient contraction of the magnetic gradient tensor;Laplace signal

P3

A

1003-2029（2011）04-0105-04

2010-12-05

王磊（1978-），男，博士，主要从事北斗系统数据处理研究。