浪流耦合模式数值模拟及检验分析

张志远 ，宋顺强 ，刘 利 ，杨广文 ，张 权 ，王 燕

（1.清华大学计算机科学与技术系，北京 100084；2.清华大学地球系统科学研究中心地球系统数值模拟教育部重点实验室，北京 100084；3.海军海洋水文气象中心，北京 100161）

浪流耦合模式数值模拟及检验分析

张志远1,2,3，宋顺强1,2，刘 利2，杨广文2，张 权3，王 燕3

（1.清华大学计算机科学与技术系，北京 100084；2.清华大学地球系统科学研究中心地球系统数值模拟教育部重点实验室，北京 100084；3.海军海洋水文气象中心，北京 100161）

基于波致混合理论，采用MASNUM海浪模型和POM环流模型建立的浪流耦合模式系统，模拟了2011年6月8日-11日中国海区对热带风暴“莎莉嘉”的响应过程，模拟结果显示波高和波向变化趋势与热带风暴的螺旋结构特征相符；利用中国海区Argo浮标温度观测，对2010年7月-12月模拟结果检验，比较表明模拟结果与观测吻合较好，细致地刻画出海温的分布和垂向结构，平均误差在0.65°以下并在各个季节上无显著的季节变化。该工作对建立新一代海洋数值预报系统有一定借鉴意义。

浪流耦合；波致混合；温度剖面；检验

对海上作业设备、舰艇和潜艇等来说，准确模拟海洋对剧烈天气变化的响应和精确刻画海洋垂直混合层、跃层分布是非常重要的。海洋的浪、潮、流等动力学过程既相互独立，具有各自动力特点和物理过程，又相互作用，通过涡动实现动量和热量上下输送。因此考虑不同的垂向混合过程，发展耦合数值模式,才能完整刻画海浪、潮流及环流之间的相互作用，准确模拟海洋要素的分布和垂向结构。

耦合模式从建立到完善，分为数学理论推导、物理参数化方案选择、耦合方案构建、数值模拟与检验分析等步骤。袁业立等[1]和Qiao et al[2]在海洋动力系统框架下提出了波浪运动混合的理论框架，解析给出波浪对环流混合作用的表达式BV。基于此波致混合理论，夏长水等[3]基于MASNUM(KeyLaboratory ofMarine Science and Numerical Modeling)[4]海浪模式和普林斯顿三维斜压海流模式POM（Princeton Ocean Model）建立了浪流耦合模式。Songet al[5]基于MASNUM海浪模式和大气-海浪环流耦合模式FGCM建立了大气-海浪-环流耦合数值模式。Wanget al[6]对浪流耦合模式实现并行并得到较好加速比。孙玉娟等[7]利用Jason-1卫星数据和NDBC浮标数据中的海浪波高观测对波高预报结果进行了比较检验。尹训强等[8]完成了对亚丁湾海域数值预报与Argo观测温度比较研究。

本文第二部分是浪流耦合模型介绍；第三部分是利用该耦合模型模拟了2011年途径南海海域热带风暴“莎莉嘉”，利用Jason-1高度计资料检验了该模型对剧烈天气过程的响应；第四部分利用中国海区的ARGO浮标数据中的温度观测，对模式输出进行了自2010年6月1日到2010年12月31日24 h模拟结果的比较检验，以验证耦合模式的准确性和稳定性。

1 模式介绍

1.1 海浪模式

MASNUM海浪模型属于第三代海浪数值模式，其空间取经纬线平行线剖分，格点上的波数空间采用极坐标方案，建立了海浪谱能量平衡方程[4]：

波数空间划分为：

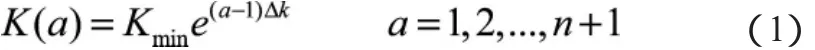
式中：Kmin为最小划分波数值（如Kmin=0.007 1）；Kmax为最大划分波数数值（如Kmax=0.689 4）

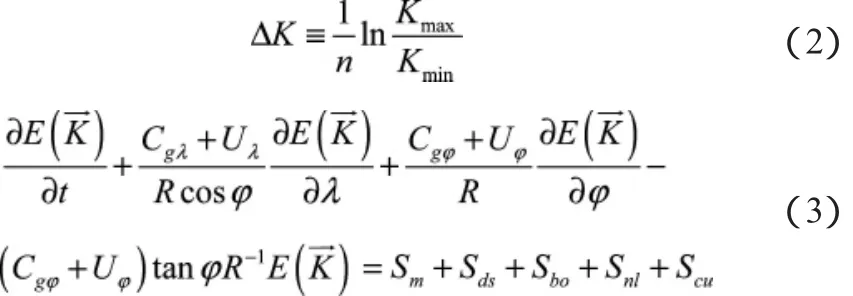
模式积分计算采用沿着球坐标系下的复杂特征线嵌入计算格式，海浪模型设置的范围是西北太平洋海域(0°N～50°N,99°E～150°E)，水平分辨率分别是(1/8)°×(1/8)°，模式输出参数包括：有效波高HS，谱峰周期TP，跨零周期TZ，主波向TH及波浪搅拌混合系数BV。

1.2 环流模式

由于关注近海海域海洋环境要素的数值模拟，采用POM环流数值模式，该模型垂向采用σ坐标，能够很好地刻画近岸地形的变化。其利用隐格式求解的Mellor-Yamada二阶湍流闭合方程[9]，从而消除时间对垂直坐标的限制，可使海洋上、下边界层的分辨率提高而保持计算稳定。水平方向采用经纬度坐标，水平有限差分格式是交错的“Arakawa C”型差分方案。水平时间差分格式是显式的，垂向时间差分格式是隐式的，后者消除了时间强迫，使表面和底边界得到更好的解决方法。

模式采取自由表面和内外模态分离的时间步长，外模态为二维并采用较短的时间步长，内模态为三维并采用较长的时间步长。模式主要输出参数包括模式区域内随时间变化的水位、三维海温、盐度和海流。模拟区域为中国海区海域(15°N～41°N,105°E～135°E)，水平分辨率是(1/24)°×(1/24)°，垂向采用σ坐标，垂直分为30层。在海洋上层采用较高的分辨率，而在海洋中、深层分辨率较低。模式的地形由全球Etopo5地形插值得到。按照Mellor的做法[10]，平滑地形需满足以下条件：

其中：Tpeak1表示早/晚高峰段的运行总时间；Tpeak2表示次高峰段的运行总时间；Tnormal表示白天正常峰段的运行总时间；Tthrough表示早晚低峰段的运行总时间，表示对算式进行取整。

式中：Hi+1和Hi是相邻的两个网格点的水深；平滑因子α取0.2。

模式初始温、盐场取自Levitus月平均温度和盐度，全场运动速度取零。为了减小水平斜压梯度力的误差，水平平均密度取年平均的密度场，并在进行水平斜压梯度力计算前扣除水平平均密度。热通量采用空间分辨率为1°×1°的COADS月平均统计结果[11]。

1.3 海浪-环流耦合理论

袁业立等[1]和Qiaoet al[2]发展的浪流耦合理论，将海洋流体的速度、温度和盐度场表达为平均部分和脉动部分，海洋湍流过程中速度脉动可以分解为波浪生的和环流生的两部分：

波浪对环流动量，温度以及盐度的搅拌项可写成如下形式：

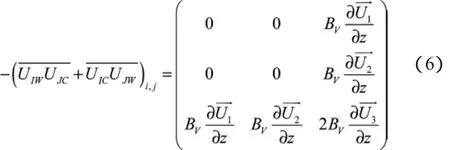
BV定义为波致混合系数，表达式为：

利用MASNUM海浪数值模式模拟波浪谱分布，利用公式（6）来计算波致混合系数，再迭加到POM模型计算出垂向涡粘系数K mC和垂向扩散系数KhC中，即：

2 热带风暴响应过程算例

本文模拟的2011年第三号热带风暴“莎莉嘉”，于2011年6月2日生成热带扰动，其后于菲律宾渐向西北移动。9日早上发展为热带低压，10日2时，发展为热带风暴。沿副热带高压西缘移动，10日10时位于广东省汕头市南偏东方大约460 km的海面上，浪高可达4 m，中心附近最大风力8级（20 m/s）,浪高可达9 m，11日凌晨到上午热带风暴“莎莉嘉”的中心在广东省沿海登陆，中心附近最大风力仍有8级（18 m/s）。

图1是浪流耦合模式在2011年6月8日12时开始模拟72 h浪高和浪向的模拟输出，每6 h输出模拟结果，从输出结果看模拟的热带风暴过境区浪高浪向趋势与实况相符，浪向与热带风暴的螺旋结构特征吻合。分析螺旋带由弱到强的演变特征，为进一步研究海洋伴随热带风暴的发生、发展和演变机理提供参考。

对以上模拟海域波高模拟值与卫星高度计（Jason_1，由美法两国发射的海洋长期观测卫星）观测值进行检验比较。散点图如图2，纵轴是观测值，横轴是模拟值，波高模拟值与观测值整体比较相近，在24 h模拟比较吻合，波高值点主要位于对角线附近，48 h，72 h模拟逐渐有些偏差。24 h模拟精度高于48 h模拟精度，48 h模拟精度高于72 h的。48 h，72 h模拟值在波高小于4 m时，偏差较小；大于4 m时，散点分布偏于红线上方，说明模拟值相对于观测值偏小。

为了检验海浪模拟的准确性，本文选用了评价模式模拟效果比较常见的检验统计参数[7,12]，包括线性回归（Linear Regression，LR）、平均误差（Mean Error，ME），绝对平均误差（Mean Absolute Error，MAE）、均方根误差（Root MeanSquare，RMS）和相关系数（Correlation Coefficient，R）等统计方法。

（1）线性回归系数：

式中：k为回归系数；c为截距。

（2）平均误差：

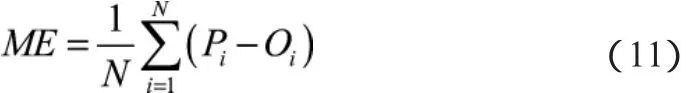
（3）绝对平均误差：

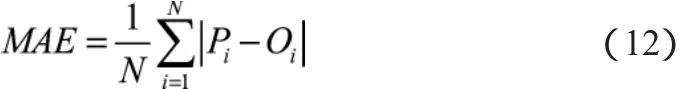
（4）均方根误差：

(5)相关系数：

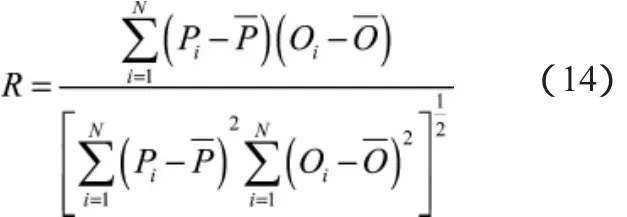
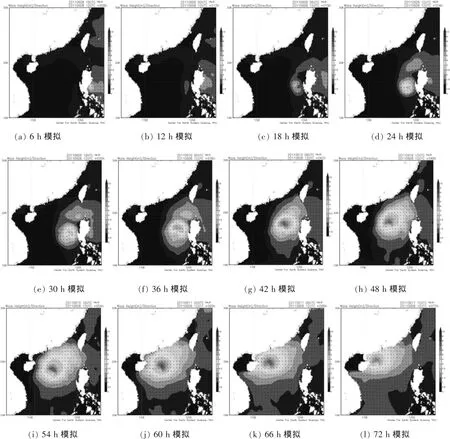
图1 2011060812启报72 h浪高和浪向模拟

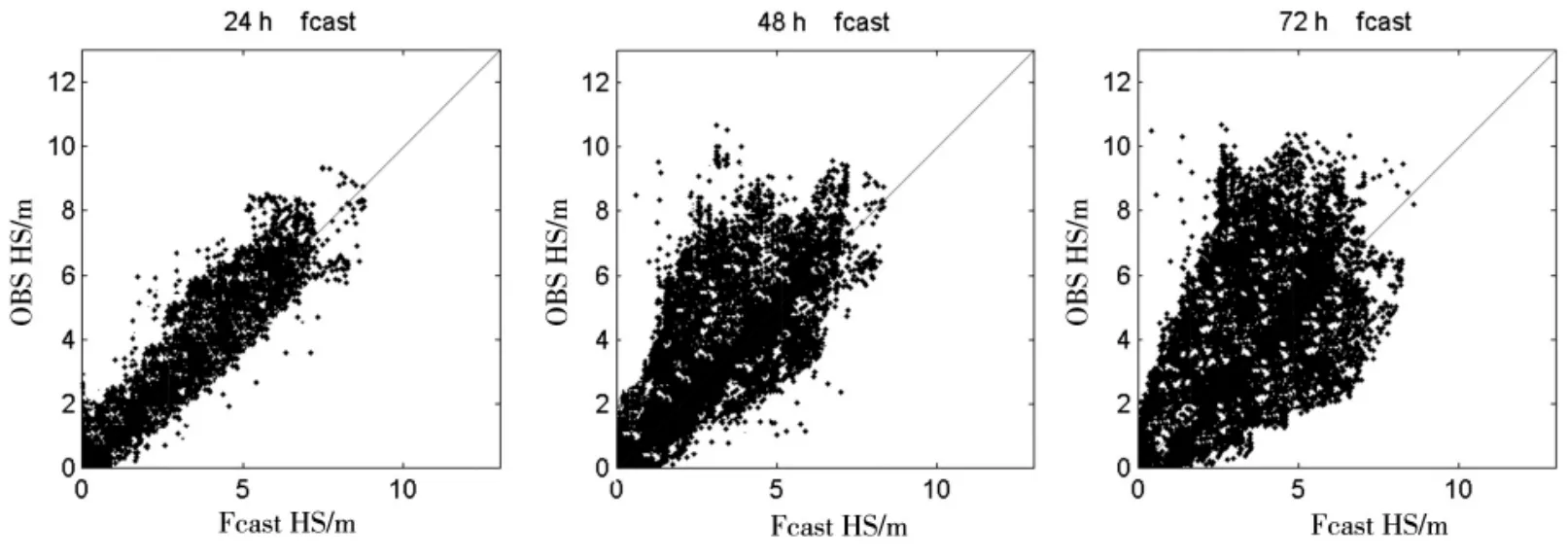
图2 模拟海区波高模拟值与卫星高度计观测值的对比

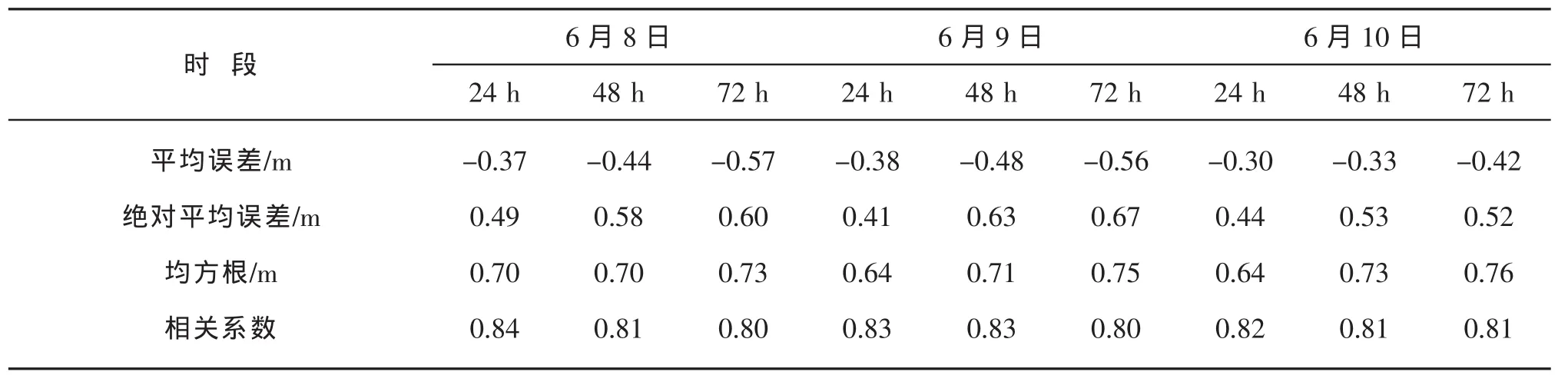
表1 模拟结果与卫星高度计观测数据的误差统计

式（1）～式（5）中，Pi为模拟值；Oi为观测值；为观测平均值；N为样本个数。

从表1的模拟结果与卫星高度计观测数据的误差统计结果分析，24 h的模拟效果要优于48 h和72 h的模拟结果，并且模拟结果比观测结果偏小。

3 温度剖面检验分析

为评估浪流耦合模式模拟效果，需要对模拟结果进行长时间跟踪检验。评价模式模拟精度主要考核准确性和稳定性。本文选取对盐度、密度和声速影响都比较大的剖面温度作为检验目标，选取Argo（Arrayfor real-time geostrophic oceanography）剖面浮标观测的温度资料作为观测数据源，对比模式输出与实际观测值的统计结果，以分析模拟效果优劣。

Argo剖面浮标是沉浮式海洋观测浮标，可快速、准确、大范围地收集全球海洋0～2 000 m海水温度剖面资料。本文利用浮标数据进行温度的检验，数据源为法国图卢兹的Argo资料服务中心。剖面比较是一种最直接的方法，可用于考核模拟温度垂直结构与观测的一致性。为了保证分析的准确性，将模拟结果插值到Argo观测位置，然后在观测位置上进行比较。中国海区的Argo观测位置如图3所示。

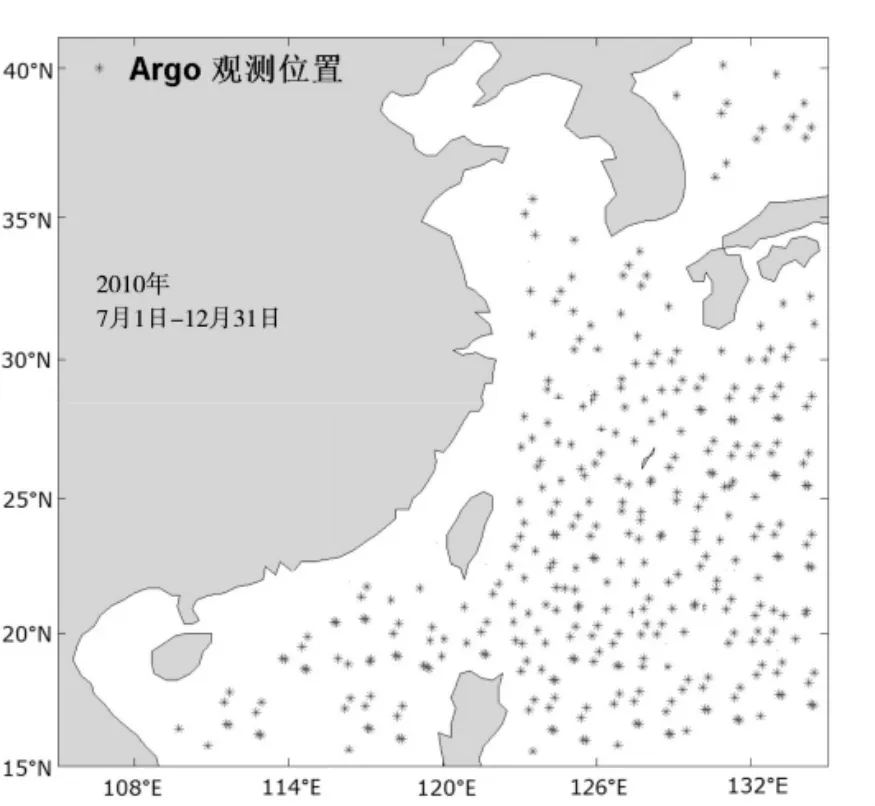
图3 中国海区Argo浮标观测位置

本文对2010年7月—12月中国海区24 h，48 h，72 h模拟时效的剖面海温开展精度检验。图2中选取7月，9月，11月三个月上旬作为分析时间段，红点表示Argo观测温度，蓝点为模拟温度，Y轴为垂向水深，X轴为温度。对比检验结果表明，模拟海洋温度结构与Argo观测较为吻合，准确刻画了海水温度剖面分布和垂向结构。由表2看出，模式模拟结果与Argo实际观测温度相关系数在0.98～0.99之间，平均误差在0.65°以下，且在各个季节上无显著的季节变化，达到海洋预报对海温数值模拟准确稳定的要求。

图4 中国海区Argo浮标观测和模拟温度剖面比较

4 结论

本文使用浪流耦合模式，成功模拟了中国海区在热带风暴“莎莉嘉”过境时的响应过程，波高和波向的模拟与螺旋带的演变吻合，24 h模拟的漩涡移动路径与热带风暴路径相符，48 h，72 h模拟路径结果有些偏差；通过模拟海区海浪波高模拟值与卫星高度计观测值的对比分析可知，24 h的模拟效果较好，而48 h，72 h的模拟值相对于观测值偏小。通过对2010年下半年的24 h，48 h和72 h模拟结果与Argo浮标观测的比较检验表明，该浪流耦合模式准确地刻画了海温的分布和垂向结构，24 h模拟效果稳定准确。

本文使用的耦合模块选用异步数据传输方式，可能会引起浪流耦合模式不能再现物理过程实时交互的效果，因此在接下来的工作中，将利用自行研制的耦合器以同步耦合方式实现耦合数据交换，提高输出时步，进而通过敏感性试验验证同步与异步耦合方式对较长时效模拟准确性的影响，完成对海洋中上层各种尺度物理过程相互作用的准确模拟分析。

[1]袁业立,乔方利,华锋.近海环流数值模式的建立I海波的搅拌和波流相互作用[J].水动力学研究与进展（A辑）,1999,14(4B)：1-8.

[2]QIAOF,YUANY,YANGY，et al.Wave-induced mixing in the upper ocean：Distribution and application to a global ocean circulation model[J].Geophys Res Lett,2004,31：L11303.

[3]夏长水.基于POM的浪流耦合模式的建立及其在大洋和近海的应用[D].青岛：中国海洋大学,2005.

[4]杨永增,乔方利,赵伟，等.球坐标MASNUM海浪数值模式的建立及其应用[J].海洋学报,2005,27(2)：1-7.

[5]SONGZ,QIAOF,YANGY，et al.An improvement of the toocold tongue in the tropical Pacific with the development of an ocean-wave-atmosphere coupled numerical model[J].Progress in Natural Science,2007,17(5)：576-583.

[6]WANGG,QIAOF,XIAC.Parallelization ofa coupled wave-circulation model and its application[J].Ocean Dynamics,2010,60(2)：331-339.

[7]孙玉娟,乔方利,王关锁，等.MASNUM海浪数值模式业务化预报与检验[J].海洋科学进展,2009,03：1671-6647.

[9]MELLORG,YAMADAT.Development of a turbulence closure model for geophysical fluid problems[J].Reviews of Geophysics and Space Physics,1982,20：851-875.

[10]BLUMBERGA,MELLORG.ADescriptionofathree-dimensionalcoastalocean circulation model[R].Washington D.C：American GeophysicalUnion,1987：21-26.

[11]ARLINDOSILVA,YOUNGC,LEVITUSS.1994AtlasofSurface Marine Data[M].Volumes 1-5,NOAA/NESDISAtlases 6-10,U.S.Department ofCommerce,NOAA,NESDIS，1994.

[12]裘国庆.数值天气预报标准化检验方法[J].气象，1989,15(9)：48-50.

Numerical Simulation and Verification of the Wave-Circulation Coupled Model

ZHANG Zhi-yuan1,2,3,SONG Shun-qiang1,2,LIU li2,YANG Guang-wen1,2,ZHANG Quan3,WANG Yan3
(1.Department of Computer Science and Technology,Tsinghua University,Beijing 100084,China;2.Ministry of Education Key Laboratory for Earth System Modeling,Center for Earth System Science,Tsinghua University,Beijing 100084,China;3.Hydrometeorological Center of Navy,Beijing 100161,China)

Based on the theory of wave-induced mixing,the wave-circulation coupled model is established,which incorporates the MASNUM wave model and the Princeton Ocean Model.It is simulated the response of oceanic elements to the tropical storm 05W.Sarika from June 8 to June 11 in 2011.The development of wave height and direction tallies with the evolution storm’s spiral bands.The Argo profiling float temperature data are used to verify the simulation results from 1st June to 31st December 2010.It is shown from the verification that the simulations are well consistent with the observation.The results describe the distributions and vertical temperature structures in precise term.The mean error between the simulation and the measured is less than 0.65°and don’t vary obviously in any seasons.The results might be useful in setting up a new ocean prediction system.

wave-circulation coupled;wave-induced mixing;temperature profile;verification

P7

A

1003-2029（2011）04-0087-06

2011-07-25

国家高技术研究发展计划资助项目(2010AA012302，2010AA012301，2010AA012400)

张志远(1978-)，男，工程师，博士研究生，研究方向为数值预报及并行耦合技术。Email：13811119180@139.com