筒型基础竖向极限承载力分析

邓 凯 ，余建星 ，乔晓国 ，尹汉军，周全智 ，姚 涛

(1.天津大学建筑工程学院，天津 300072；2.海洋石油工程股份有限公司，天津 300451)

筒型基础竖向极限承载力分析

邓 凯1，余建星1，乔晓国1，尹汉军2，周全智1，姚 涛2

(1.天津大学建筑工程学院，天津 300072；2.海洋石油工程股份有限公司，天津 300451)

结合最新研究成果，编制了筒型基础竖向极限承载力计算程序，可根据土壤参数和承载能力要求确定筒型基础的主要尺寸；同时使用ABAQUS和ANSYS软件建立筒型基础有限元模型，采用非线性接触方法模拟筒-土的边界，计算筒型基础的竖向极限承载力，两种软件的计算结果和编制程序的计算结果基本相同；最后对影响筒型基础竖向极限承载力的土壤参数进行了分析。

筒型基础；承载力；接触；有限元

筒型基础技术研究开始于20世纪50年代，最初应用于系泊的吸力锚桩，在很多锚泊系统中得到成功的运用。在20世纪90年代开始把它运用到平台基础上，起初用做平台锚固，接着又用作导管架平台的基础。伴随着油气开发向深海发展，筒型基础主要是作为深海浮式平台的系泊形式和水下生产系统的基础形式。目前，筒型基础由于适用的土质范围、水深范围及环境荷载相当宽广，正成为海洋工程结构的主要基础形式。

作为深海水下设施基座，最主要的设计指标是竖向极限承载力。目前地基设计承载力有两类，一是地基容许承载力，二是地基承载力设计值。确定地基承载力的方法有：理论公式计算法、现场原位试验法、地基规范查表法，随着计算技术的发展，有限元分析方法也可用于地基承载力的分析计算。根据相关规范编制筒型基础竖向承载力和贯入阻力的程序，可用于筒型基础初步设计，并结合ABAQUS和ANSYS有限元计算软件对筒型基础的竖向极限承载力进行对比校核。

1 筒型基础承载力的规范计算方法

筒型基础贯入分为自重贯入和负压贯入两种阶段，一般情况下，筒型基础的安装需要这两种方法先后使用。筒型基础先靠自身的负重贯入到一定深度后，再借助负压的作用，达到预定的贯入深度。在施加负压的过程中，对土体产生的扰动与自重贯入下对土体产生的扰动不同，直接导致筒型基础在位承载力的不同。

1.1 自重贯入深度

（1）桩的竖向极限承载力QD的计算公式由文献[4]中给出：

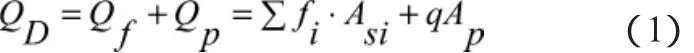
式中：Qf为表面摩擦阻力（kN）；Qp为端部总承载力（kN）；fi为第i层土的单位侧摩阻力（kPa）；Asi为第i层土中桩侧表面积（m2）；q 单位桩端承载力（kPa）；Ap为桩端总面积（m2）；

（2）对于在粘土中筒型基础，筒体上任何一点的单位侧摩阻力 f，可用（2）式计算：

式中：α为无量纲系数；c为相应点土壤的不排水抗剪强度（kPa）。

系数α由（3）式计算可得：

限制条件为α≤1.0。式中：ψ=c/P'0，P'0为相应点的上覆土压力（kPa）。

（3）对于端部支承在粘性土中的筒型基础，单位端部承载力q由（4）式计算，其单位为kPa：

对于在砂土中的筒型基础，筒体上任何一点的单位侧摩阻力 f，可用（5）式计算：

式中：K为侧压力系数；P0'有效上覆土压力（kPa）；δ为土和筒壁之间的摩擦角，即土的外摩擦角。

（4）对于端部支承在非粘性土壤中的筒型基础，单位端部承载力q可由（6）式计算，其单位为kPa：

式中：P'0为筒端处的有限覆盖压力（kPa）；Nq为承载力系数。

筒型基础靠自重一般不能完成整个贯入过程，而是由后续施加的负压来完成最终的贯入，所以自重贯入深度范围内仅有由于侧摩阻力导致的承载力，没有端部承载力。

1.2 负压贯入深度

砂土不存在固结问题，所以负压贯入深度范围内承载力与自重贯入深度范围内的承载力并无区别，对于沿筒长任何一点的砂土单位侧摩阻力τ，可采用（1）式计算。

粘土由于触变性和孔隙水压力的消散，其抗剪强度有所提高，筒型基础的承载力也相应提高。由于筒内、外土排水条件的差异，其抗剪强度比值α，α=SURR/SUDSS（重塑再固结土的不排水抗剪强度/原土的不排水抗剪强度）也会有所不同。

对于正常固结的筒外粘土在负压贯入作用下，经过两个月完成了90%的孔隙水压力消散后，由于土体中有效应力的变化和土体本身存在的触变性，重塑区土体的抗剪强度不会恢复到贯入前的水平，并且出现一定的折减，根据土性质的不同（体现在土的灵敏度St和塑性指数Ip），可以得到不同的抗剪强度比值，如表1[3]。

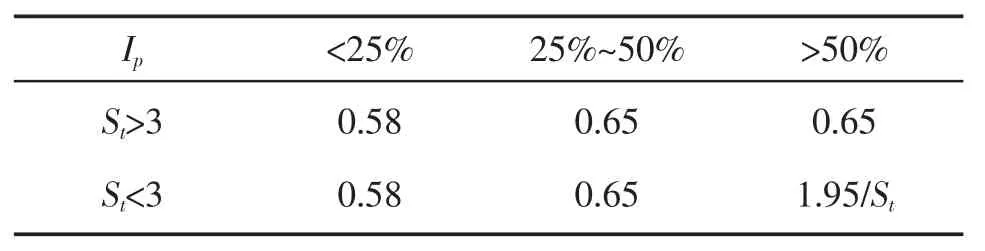
表1 筒外粘土在负压贯入下的抗剪强度比值

同样的对于正常固结的筒内粘土，不存在环状加强筋的情况下，筒内重塑区中的粘土在经过一段时间的排水固结或者是由于触变性，其抗剪强度比值会根据土性质的不同（体现在土的灵敏度St和塑性指数Ip）而不同，如表2[3]。

表2 筒内粘土在负压贯入下的抗剪强度比值

负压贯入下粘土中筒内外壁单位面积的摩擦力可使用（2）式计算，但筒内、外壁的α需要根据灵敏度和塑性指数查表1、表2选取。

1.3 自编程序

依据上述关于海底基础的设计方法使用MathCAD编制程序，计算给定尺寸筒型基础在特定土层中的贯入深度、贯入阻力以及极限承载力，也可用于筒型基础的初步选型。程序分为粘土模块和砂土模块，可根据设计土层分布随意组合，粘土模块和砂土模块中的计算公式不同，但程序流程相同，见图1～图3。

1.4 算例

算例的筒型基础的基本尺寸为直径4 m，总长12 m，贯入深度为11 m，壁厚为15 mm，筒型基础自重400 kN，地质资料如表3所示，计算筒型基础在位时的竖向极限承载力。

根据自编程序得到各层土的计算结果见表4。

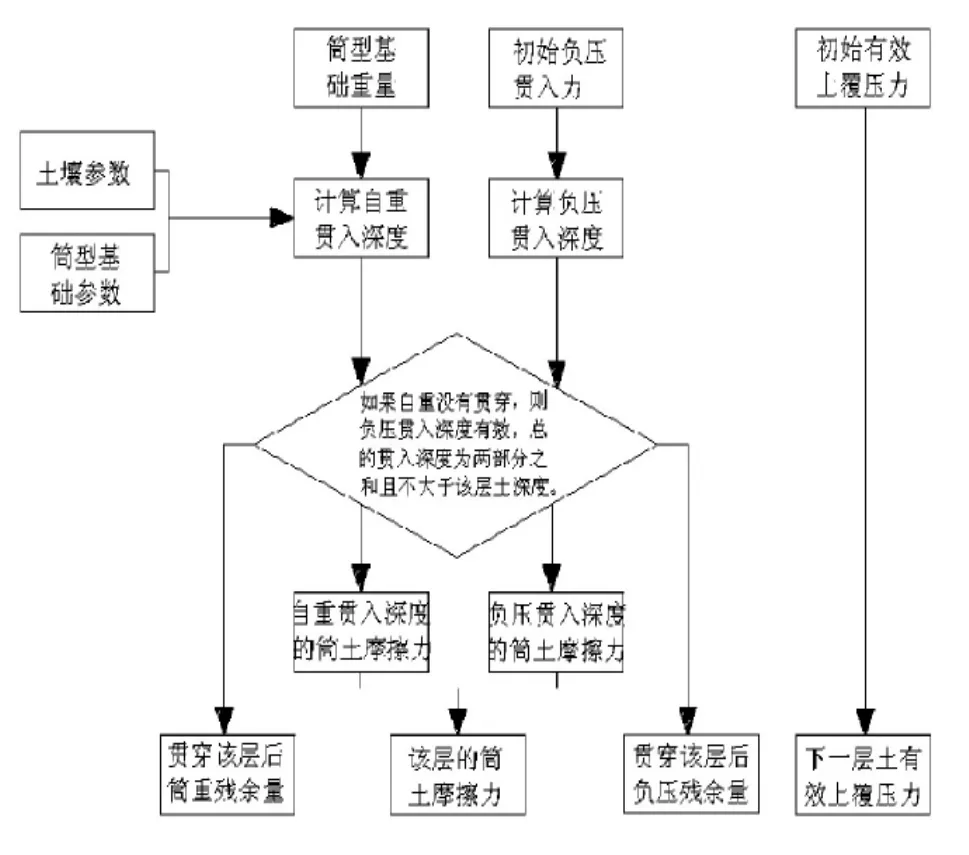
图1 第一层土中的计算流程

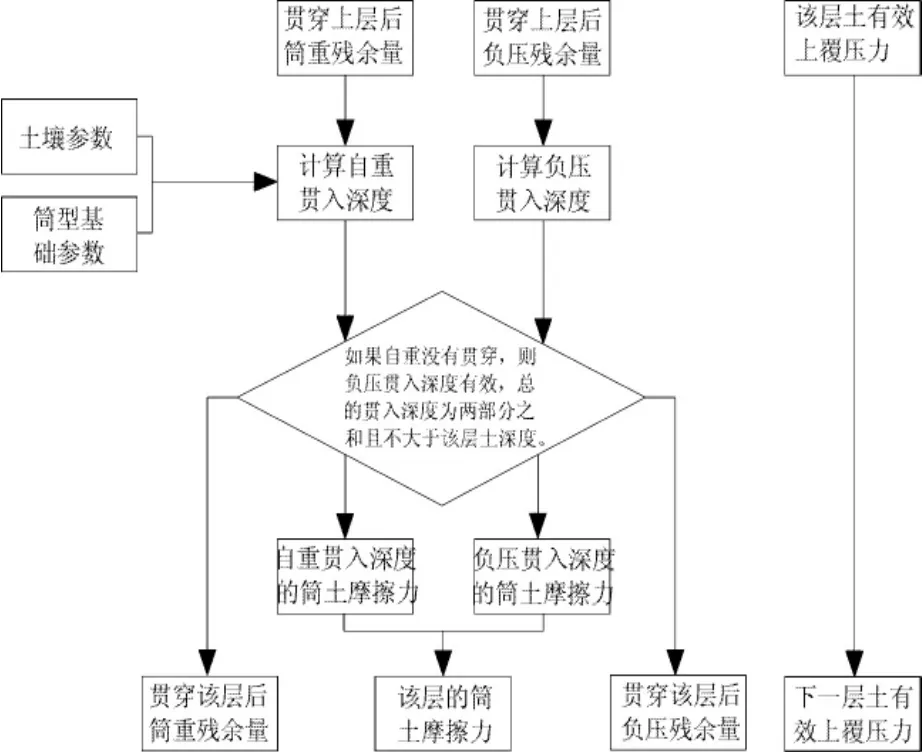
图2 其余层土内的计算流程

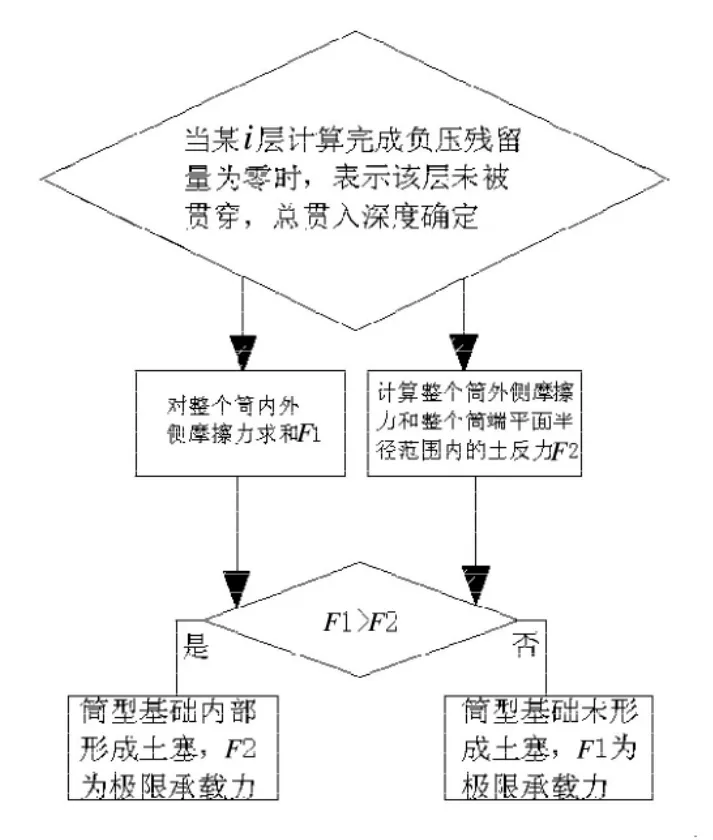
图3 结束层

表3 海底土层实测资料

表4 各层土的计算结果

筒型基础自重贯入5.856 m（各层自重贯穿深度之和），达到最终贯入深度需要施加负压力1 100 kN，土体完成固结后筒型基础的承载力为1 723.6 kN（各层侧壁摩擦力之和）。

2 极限承载力的有限元分析

使用通用有限元计算软件ABAQUS和ANSYS对上述例子中筒型基础的极限承载力进行分析，并将其与规范方法的计算结果进行对比分析。

考虑结构的对称性，采用一半模型。根据筒型基础的尺寸大小，模型选用：土层半径2.5D=10 m，土层高度2H=25 m。在对称面上设置对称约束，在土层侧面设置除了高度方向的约束，在土层的底面设置全约束，筒土界面采用接触的方法进行处理，见图4。

图4 接触对设置

接触面分析对于筒型基础承载能力的有限元分析至关重要。对于粘土而言，由于在贯入过程中重塑区的土发生重塑导致再固结后，抗剪强度降低，从而低于完好土体的抗剪强度，而重塑区只是筒土界面的一个薄层，厚度不超过筒的厚度；对于砂土而言，虽然在贯入过程中，不会发生土体重塑导致抗剪强度降低，但是筒土之间的摩擦角小于土的内摩擦角，也就是说筒土界面的强度小于土本身的强度，所以可以认为筒土接触面的破坏是先于土体破坏的。也就是说，一旦筒土接触面发生了整体滑移即接触面上的摩擦力已经达到最大值，筒型基础便达到了其极限承载力。

土体在贯入开始之前内部存在自重造成的应力场，该应力场作为初始条件必须正确施加，可通过地应力平衡法进行该初始条件的加载，地应力平衡之后的土体位移如图5和图6所示。

图5 ABAQUS土体位移计算结果

图6 ANSYS土体位移计算结果

由图5、图6，可见两种软件的土体位移计算结果为1.704×10-3mm和0.135×10-3mm，远远小于模型的尺寸，可以认为地应力平衡的效果很好。

在完成地应力平衡之后，土体中竖向应力分布见图7、图8。

图7 ABAQUS土体竖向应力计算结果

图8 ANSYS土体竖向应力计算结果

从图7、图8中可以看出地应力平衡后土体中的应力与天然地基应力分布呈现相同的分层现象。

在地应力平衡完成后，筒-土接触面上已经产生了接触应力，由于接触应力和土体竖向应力间存在线性关系，所以接触应力也出现分层的现象，且随着土体深度的增加而增长，如图9和图10。

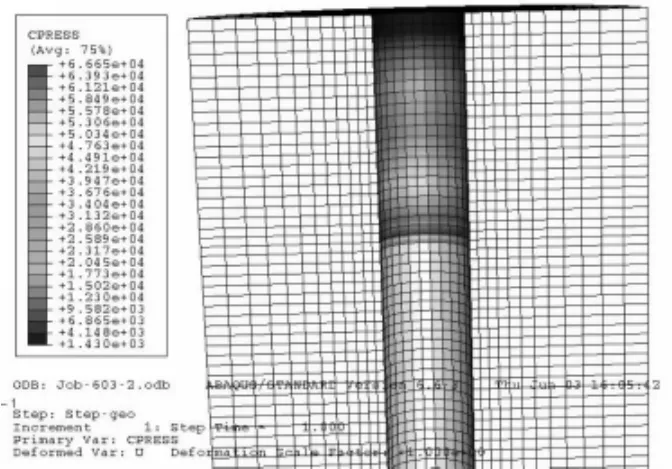
图9 ABAQUS接触应力计算结果

图10 ANSYS接触应力计算结果

在程序中分为3个载荷步进行计算。在初始载荷步中完成了对模型边界和接触条件的设置，并且在提交计算时，计算程序会根据所设的参数调整接触面上的接触对；在第二个载荷步中，对模型施加重力，配合添加的命令行和输入文件，完成对地应力的平衡过程；在第三个载荷步中，添加工作荷载，采用线性加载的方式，即荷载和时间呈线性关系而逐步增大，直至荷载添加至极限值。

在ABAQUS和ANSYS中，当筒土接触达到其极限值后，筒体便会出现刚体位移，此时筒型基础即达到极限承载力状态。对于例中加载1 200 kN（有限元模型只有半个筒）竖向载荷，ABAQUS计算载荷因子达到0.722 6，而ANSYS中则为0.723，两者十分接近，将计算时间换算成筒形基础承载力，并且与自编程序进行对比，可得表5。

表5 承载力比较/kN

ABAQUS和ANSYS两者之间结果十分接近，同时与规范解相差在1%左右，可以看出有限元方法进行筒型基础承载力的计算是可行的，规范方法不能计算筒型基础受轴向偏心载荷、水平载荷以及弯矩作用下的极限承载力，有限元方法可以解决这个问题，所以可以作为规范方法的补充。

3 土壤参数对承载力的影响

塑性指数Ip是反映土的塑性的重要参数，土的塑性指数越大塑性也越大。灵敏度St是反映土结构性的参数，土的灵敏度越高，其结构性越强，受扰动后土的强度降低的就越多。当筒型基础位于粘土层时，分析了粘土数据中塑性指数Ip和灵敏度St对筒型基础承载力的影响。表6是自编程序对算例中筒型基础及土参数计算所得的随粘土灵敏度和塑性指数变化的承载力。

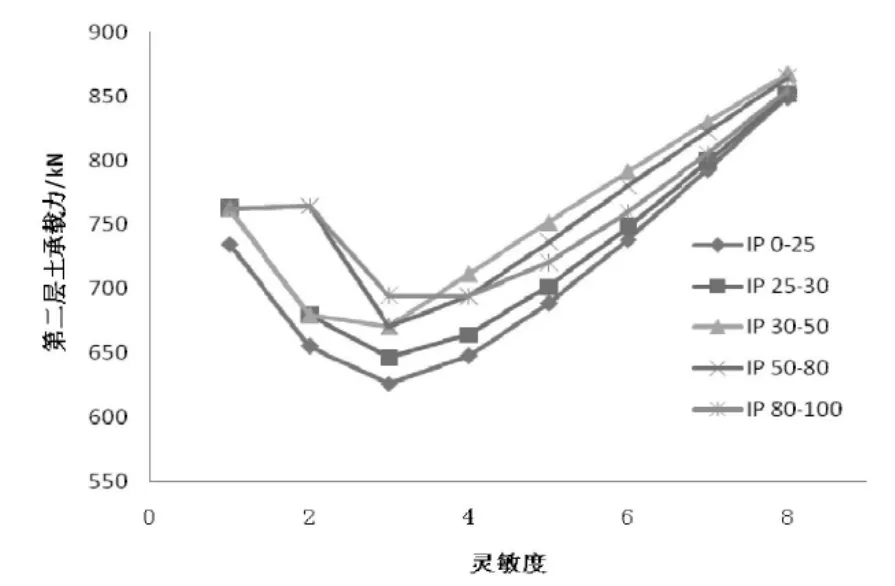
图11 粘土灵敏度和塑性指数对地基承载力影响曲线

从表6和图11中可以看出，针对该土层分布，自重贯入深度在粘土层中，粘土层灵敏度为3时承载力最小；在灵敏度相同的情况下，粘土层的承载力在塑性指数为30～50时

最大。粘土层灵敏度影响粘土层承载力，由于总的贯入深度是固定的，所以第1层和第3层砂土的承载力并没有变化。而随着粘土灵敏度的增大，贯入计算中筒侧摩阻力减小，筒型基础在粘土中自重贯入深度增加，而负压贯入深度相对减少，自重贯入范围内相同贯入深度所能提供的承载力要比负压贯入范围内的要大，所以灵敏度增大导致粘土层以及总的承载力增大。

表6 不同灵敏度和塑性指数下粘土的承载力

4 结论

借鉴国内外的最新研究成果，结合相关规范，对筒型基础竖向极限承载力进行了深入研究，根据相关研究成果自编了筒型基础承载力计算程序，并且运用有限元软件进行对比验证，得出以下结论：

（1）根据土力学相关理论以及船级社的推荐做法，研究了筒型基础外型尺寸与承载力的内在关系，自编了筒型基础承载力计算程序，使用时，仅需输入各层土壤参数即可得到设计尺寸的筒型基础的极限承载力，可以用于筒型基础的初步选型。

（2）通过设置接触面属性来模拟筒-土之间的滑移破坏，采用地应力平衡模拟初始地应力状态，根据规范方法计算结果和有限元软件ANSYS，ABAQUS分析结果的对比，表明这种模拟方法是合理可行的。

（3）当筒型基础自重贯入深度在粘土范围内时，灵敏度影响筒型基础自重贯入深度，从而影响筒型基础在粘土范围内的承载力；塑性指数在30～50之间时，负压贯入深度内的承载力是最高的。

[1]陈仲颐，周景星，王洪瑾.土力学[M].北京：清华大学出版社，1994.

[2]吴梦喜，时忠民.桶形基础的承载特性与承载力计算[J].中国造船，2003（Z1）：441-446.

[3]DETNORSKE VERITAS.DNV-RP-E303.Geotechnical design and installation ofsuction anchors in clay[S].Norway：GANGrafisk,2005-10-1.

[4]API-RP2A WSD：Recommended Practice for Planning，Designing and Constructing fixed Offshore Platforms Working Stress Design[S].21st Edition，2000.

[5]费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2010.

[6]祝效华，余志祥.ANSYS高级工程有限元分析范例精选[M].北京：电子工业出版社，2004.

Vertical Ultimate Bearing Capacity Analysis of Bucket Foundation

DENG Kai1,YU Jian-xing1,QIAO Xiao-guo1,YIN Han-jun2,ZHOU Quan-zhi1,YAO Tao2
(1.School of Civil Engineering,Tianjin University,Tianjin 300072,China;2.Offshore Oil Engineering Co.Ltd,Tianjin 300452,China)

Combining the newest research achievement,the bucket foundation vertical ultimate bearing capacity calculating program(“Program” for short)can be used for the primary dimensions design of bucket foundation depending on the soil property and bearing capacity.The finite element model(FEM)is established with ANSYS and ABAQUS,the interface of the bucket and soil is simulated with non-linear contact method,the result of the vertical ultimate bearing capacity of bucket foundation with FEM and the Program are almost the same.At last,the soil property which affects the vertical bearing capacity of the bucket foundation is discussed.

bucket foundation;ultimate bearing capacity;contact;finite element method

P75

A

1003-2029（2011）04-0096-06

2011-04-01

邓凯（1978-），男，在读博士，研究方向为船舶结构可靠性。Email：juwosuozhi@sina.com