近海海洋水体光散射特性研究——以蓬莱近岸海域为例

韩 冰，李铜基，朱建华

（国家海洋技术中心，天津 300112）

近海海洋水体光散射特性研究
——以蓬莱近岸海域为例

韩 冰，李铜基，朱建华

（国家海洋技术中心，天津 300112）

对水体散射特性的分析方法进行了研究，并以蓬莱附近海域水体为例对方法进行了验证。从分析结果可以看出，烟台蓬莱附近海域水体散射占据主导，单次散射反照率ω0在0.6～0.8之间变化，且后向散射比例Bp在0.08～0.17间变化，虽高于Mobley给出的0.03的上限，但与Mie理论模拟计算的结果相吻合，属于具有强后向散射特征的II类水体；该区域的粒子折射指数*np高于1.15，说明水体具有典型的矿物质颗粒特征。通过对实测数据的分析发现，文中提出的方法适合于我国近岸水体，可为研究我国近岸水体的水体散射特性提供借鉴。

水体散射；折射指数；后向散射比例；单次散射反照率；蓬莱

海水散射特性的测量与研究有利于揭示区域性海洋水色形成机理以及开发区域性水色生物－光学应用算法。当光入射到水体时，水中不同物质的折射指数np不同，导致在界面处形成反射与折射作用并改变了由一个介质透射到另一个介质的辐射亮度场[1]。虽然水温、盐度和压力对折射指数np有影响，但对折射指数np起决定性作用的是各成分的类型与浓度。介质折射指数的实部决定了该介质的散射特性，而虚部决定了其吸收特性[2]。

入射光受到水体成分的吸收和散射的影响，其中一部分被后向散射出海面，给人们从视觉上呈现出海水的颜色。水色遥感卫星就是通过感知这部分离水辐射量，从而实现对水体主要成分类型和浓度的探测。太阳光从某一角度射入海水经过水中物质的吸收和散射后形成一个散射光场（图1）。散射光场的形成遵循水体的辐射传输理论[3]。

图1 水中的散射光场

体散射函数β（ψ；λ）[2]描述了水体中散射光的角度分布，即：

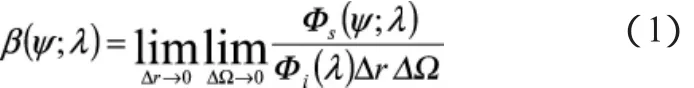
式中：Φs为散射光能量；Φi为入射光能量；Δr为径向距离；ΔΩ为立体角。而水体散射相函数是经散射系数b（λ）归一化，表征光被散射到角度ψ的概率函数（图2），即：

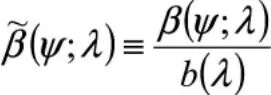
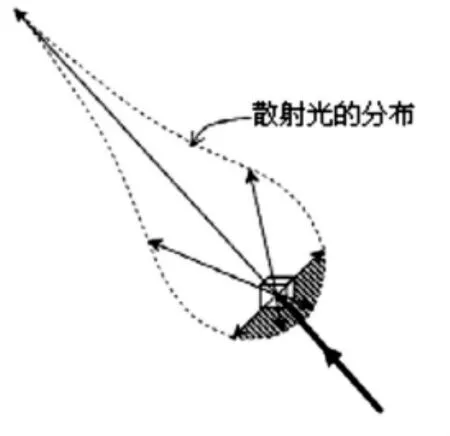
图2 散射相函数示意图

体散射函数（Volume Scattering Function,VSF）与水体吸收系数，是两个最基本的水体光学特性。Mobley等[3]指出，吸收系数和体散射函数决定了海水的固有光学特性。相比于吸收系数的研究进展，体散射函数研究却缓慢得多，一方面是由于多角度散射测量仪器的研制更具复杂性，另一方面是由于体散射的分析理论要比吸收更复杂。水体散射可以看作是水中各物质成分散射的线性叠加，与成分类型和含量存在相关关系。体散射函数描述了水中光场的分布，是研究水体光学特性不可或缺的重要参数。而散射相函数消除了体散射函数中环境不同形成的量值差异，是研究水体散射特性的理想参数。水体散射相函数 P（λ，θ）决定了水体散射系数 b（λ）、后向散射系数bb（λ）、单次散射反射率ω0、粒径分布斜率ξ、颗粒折射指数np和后向散射比Bp（λ）等重要参数。Twardowski[4]给出藻类细胞折射指数约为1.04～1.05，有机非生命物质为1.05，无机非生命物质为1.14～1.18。Jelov[5]研究认为火星浮游植物折射指数为1.01～1.09，碎石和无机颗粒物为1.15～1.20，Mobley[2]认为浮游植物的折射指数为1.05，无机颗粒物为1.16。李铜基等[6]对黄东海水体的后向散射系数进行了研究，得到了遥感反射比与412 nm后向散射系数的经验关系。宋庆君等[7]等对黄东海的水体散射特性进行了研究，得到了后向散射系数与散射系数为一种乘幂关系。崔廷伟等[8]建立了遥感反射率光谱数据与后向散射系数的反演模型。周雯[9]等利用Mie理论模型对海水中颗粒的吸收和散射特性进行了模拟计算和分析。马荣华[10]等对太湖水体的后向散射概率进行了研究，表明太湖水体的颗粒物后向散射概率可表示为波长的二次函数。然而，目前国内对水体散射特性的研究缺乏系统性和深入性，研究成果往往仅限于某个具体的区域或者某些具体的实验数据集，无法得到广泛的普及和推广。

水体散射相函数因其在水体光场研究中的重要性而被广泛研究和应用。1972年Petzold[11]对三种典型水体的水体散射测量，获得深海洁净水体、近海浑浊水体以及港口极浑浊水体的散射相函数，该结果至今仍被广泛引用。Henyey和Greenstein[12]提出的HG相函数因其形式简单而被广泛采用。其它的散射相函数还包括了Kattawar提出的三参数相函数[13]、Haltrin 相函 数[14]、Cornette-Shanks 相 函 数[15]和 Reynolds-Mc Cormick提出的两参数相函数[16]等。这些散射相函数在应用时都有一定的局限性，即不能与实际的相函数相吻合[17]。Fournier和Forand等给出的散射相函数[18]几乎能够表现所有实际的相函数，但是其复杂的理论表达形式限制了它的应用。Mobley[3]等研究了散射相函数形状对于水下辐照度和辐亮度以及反射率的影响，发现5°～90°和90°～180°范围内散射相函数的形状变化对其影响非常明显。苏丽萍等[19]假定海水中悬浮粒子的尺寸分布采用双曲线模型，利用Mie散射理论计算了海水中悬浮粒子的归一化体散射函数。詹海刚、施平、陈楚群等[20]开展的准分析算法研究时利用水分子与悬浮颗粒后向散射相函数作用的光学模型作为前向模型。目前，国内对水体的体散射函数和散射相函数的研究方面，可参考的成果较少。

我国海域水体多为II类水体，领海空间跨度大，且有广阔的大陆架及诸多河流的注入，造成水体成分类型复杂、分布区域性特点突出，因此，在我国海域开展散射特性的测量与分析研究是促进水色遥感算法开发、遥感数据应用的基础之一。

1 水体散射数据分析理论基础

水体中单色光的辐射传输方程[2]如（2）式：

吸收和散射的相对比例可用单次散射反照率ω0=b/c描述，单次散射反照率给出光子在介质中交互作用的散射概率。根据准单次散射的理论近似，遥感反射比仅与后向散射因子（或称后向散射比）B=bb/b有关，B描述了任何散射事件中，光子在散射角ψ≥90°时的概率。然而，在考虑多次散射时，所有的辐射量是基于所有散射角度范围的相函数，即相同的B值、不同的散射相函数（ψ）形状会使相关辐亮度分布不同。当然，这种差异的幅度不仅仅依赖于˜（ψ）的函数形式，还依赖于水体中多次散射的重要性（即依赖于ω0）以及如太阳天顶角等外部参数[3]。由此可见，后向散射因子与表观光学参数有着密切的关系，而同时，它又是水体颗粒物成分散射特性的指标之一。

海洋颗粒物散射的角度分布，即体散射函数，依赖于颗粒物的尺度分布和折射指数np。Twardowski[4]开发了一种由实测光谱光束衰减系数c（λ）和颗粒后向散射因子Bp估算np和ξ的方法[3]。由于仅依赖于ACS和HS6/ECO-VSF3测量的IOP数据，因此很方便。

通常粒子尺度分布的形状（PSD）可用Junge-type模型描述，即分布遵循双曲线形式，斜率为ξ，如（3）式：

式中：N（D）是颗粒直径在D～dD间的数量；D0是颗粒数量为N0的参考直径[21-22]；ξ为微分斜率参数，通常在2.5～5之间[3-4,21]，ξ越大说明粒子的平均尺度越小。

基于Mie理论分析，并将其应用到非吸收性、折射指数不变且具有幂函数粒子尺度分布的粒子时，粒子的衰减光谱可以得出如下[4,23]：

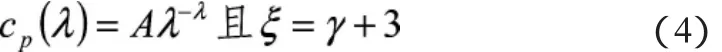
上述关系仅在粒子范围为[0,∞]时成立。

ξ与颗粒物吸收系数cp（λ）之间存在如（5）式[4,23]：

Boss[21]对上式提出了改进，认为在绝大多数情形下，（6）式是适用的。

需要提到的是，（5）式和（6）式的差项 0.5exp（-6γ）在 γ≥1.035时小于0.001，可以忽略。

Twardowski[4]根据Mie式理论开发了一个利用ξ和Bp（λ）估算np（λ）的分析模型，（7）式。

（7）式的限定条件是 2.5≤ξ≤4.5；0≤Bp≤0.3。

Fournier和Forand[18，24]给出了一种根据粒子尺度分布计算散射相函数的方法，（8）式。

根据（8）式可以通过理论计算得到粒子的后向散射比例（9）式为：

式中：δ90为 δ在 ψ=90°的值。

Mobley[3]给出了折射指数np与粒子分布斜率ξ的关系，如（10）式和（11）式：

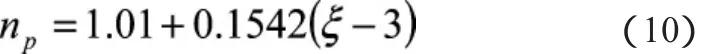
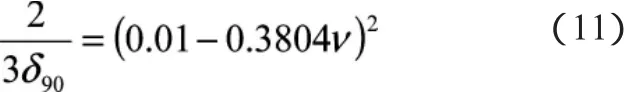
根据上述分析，利用水体的吸收系数、散射系数和后向散射系数可以获取水体后向散射比例、粒子折射指数、单次散射反照率及水体散射相函数等重要参数。这为研究水体的散射特性提供了一种简便、可操作性强的途径。

2 蓬莱附近海域水体散射特性分析

文中采用2010年8月份烟台蓬莱附近海域的试验数据对上节的散射特性分析方法应用和验证。2010年8月的试验中，测量的要素主要包括吸收、散射及辅助数据。试该验基本情况如表1所示。

表1 2010年8月蓬莱试验基本情况

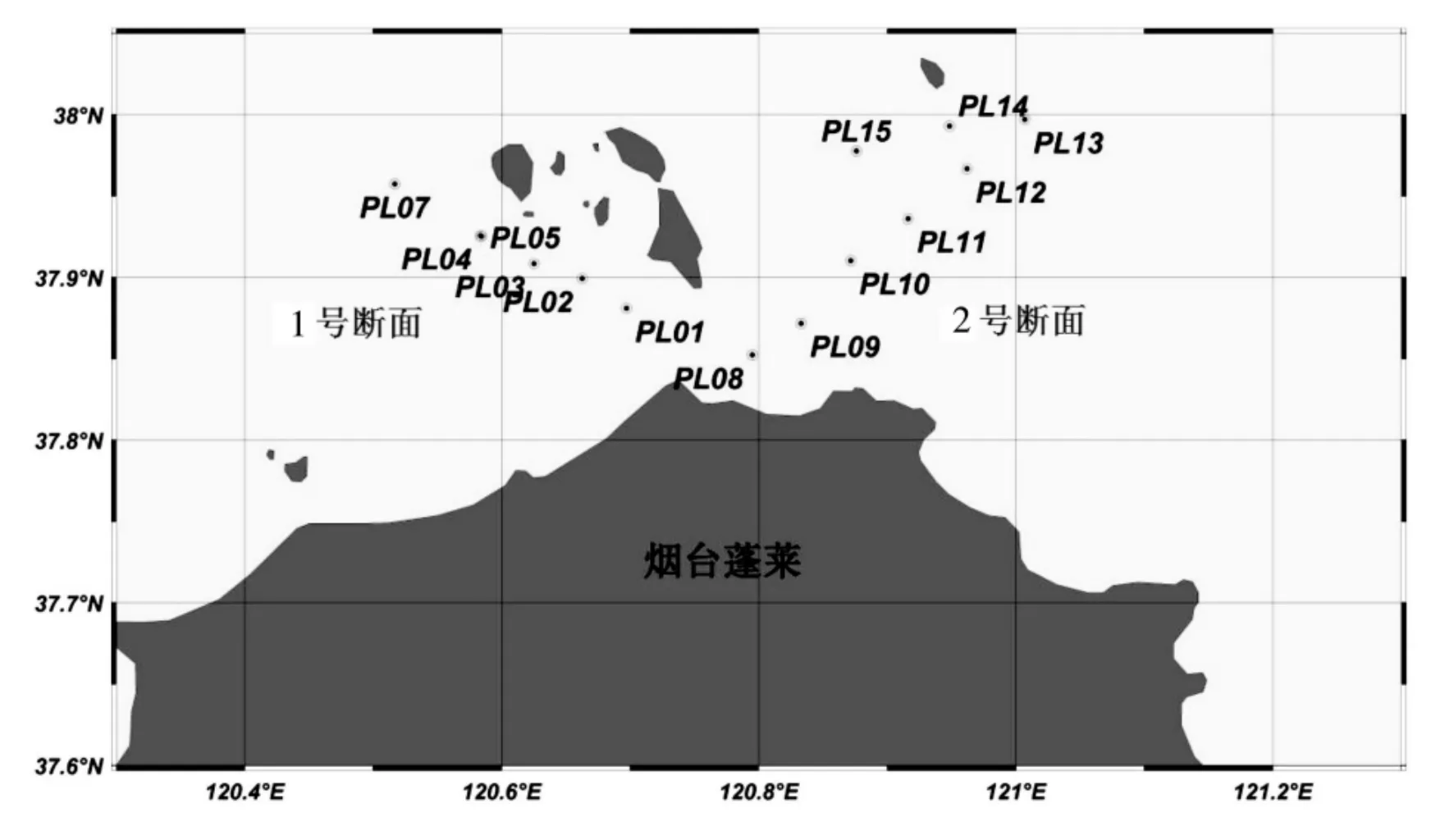
图3 烟台蓬莱试验站位图

为使试验数据能更好描述该区域的水体散射特性，共设计了两条断面，分别从蓬莱码头出发向西北方向（1号断面）和东北方向（2号断面）延伸。试验站位如图3所示。

一般来说，水体后向散射占水体总散射能量的比例很小，水中颗粒物的类型和浓度不同后向散射比例变化可达1～2个数量级。因此，为保证试验数据的质量，在水体后向散射的测量过程中，使用了两种不同类型的仪器同步测量。

通过比较发现，对于绝大多数站位，两种仪器获取的532 nm后向散射系数的相对偏差不超过20%，数据的一致性较好。为保证分析结果的准确，本文仅选用符合该标准的数据作为后续的数据分析的对象。

根据上节描述的原理和方法，利用ACS和ECO-VSF3测量的数据可以计算包括单次散射反照率ω0、粒子后向散射比例Bp、颗粒折射指数np、粒子谱分布斜率ξ等重要的光学参数。表2给出了不同站位不同水层的单次散射反照率ω0。

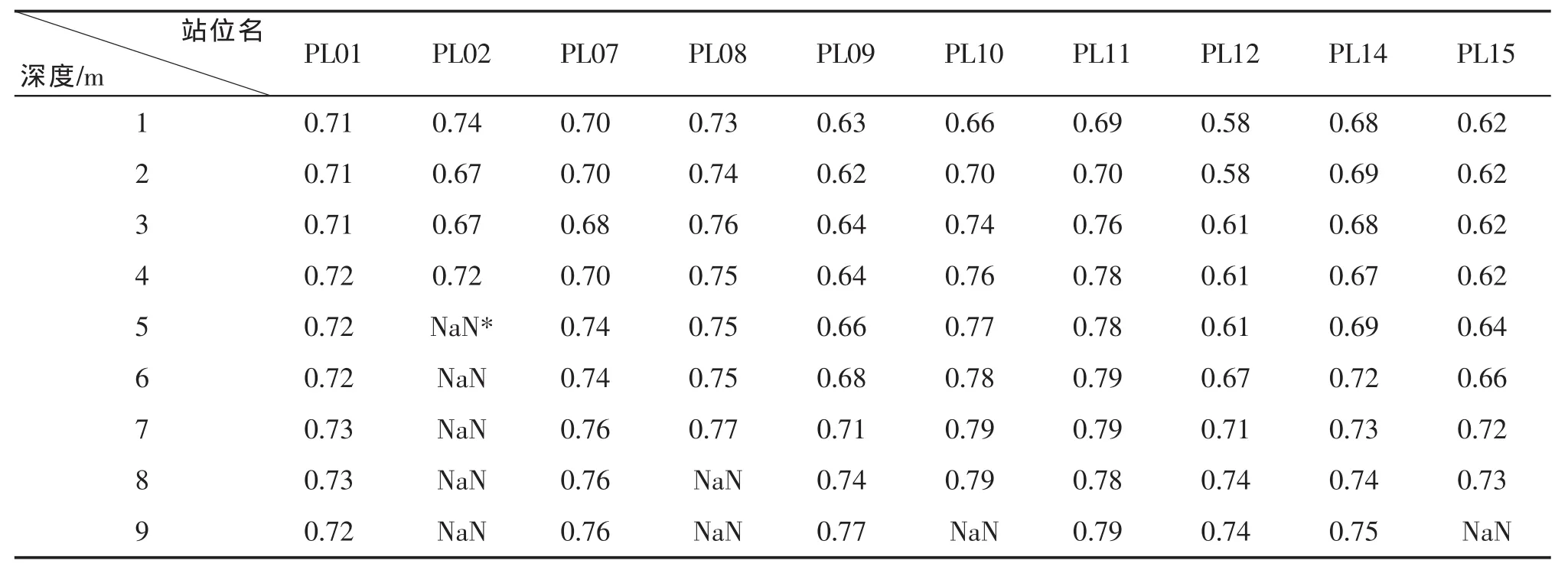
表2 各站位不同深度水体的单次散射反照率ω0

在海水中，ω0可由0.1（吸收为主水体）到0.9（散射为主水体）变化。从表2可以看出，该区域水体的ω0最小值超过0.6，最高的接近0.8，说明散射占据绝对的主导地位。对某一固定站位，绝大多数情况下ω0随深度增加而增大；而从站位间的比较来看，离岸较近的 PL01，PL02，PL08，PL09 的 ω0显著较离岸较远的PL12，PL14和PL15大。图4给出了2号断面ω0的垂直剖面分布。

从图中可以看出，对任一固定站位，ω0随水深增加而逐渐增大。然而，在不同区域，ω0随水深递增的速率存在较大差异。ω0垂直分布呈现出显著的“U”形特征。在该断面中间的站位ω0显著高于其它区域，表明该区域散射占据主导地位。

图4 2号断面单次散射反照率ω0的垂直分布，其中右图为断面站位示意图

表3 各站位不同水层的后向散射比例Bp

表3给出了不同站位不同水层的粒子后向散射比例Bp。

从表3可以看出，后向散射比例Bp最小值出现在PL12，PL14和PL15站位，均位于离岸最远且受岛屿影响最小的区域，5 m以上水层Bp约为0.08；而最大值出现在PL08站位，离岸最近，5 m以上水层Bp约为0.17。

为说明数据的合理性，图5给出了利用Mie理论模拟的粒子散射相函数，在模拟过程中，模拟波长为532 nm，介质为海水，其折射指数为1.34，粒子假设为球形，其折射指数为1.15，粒子的半径分别为 0.5 μm，0.4 μm，0.3 μm，0.2 μm，0.15 μm 和 0.1 μm。

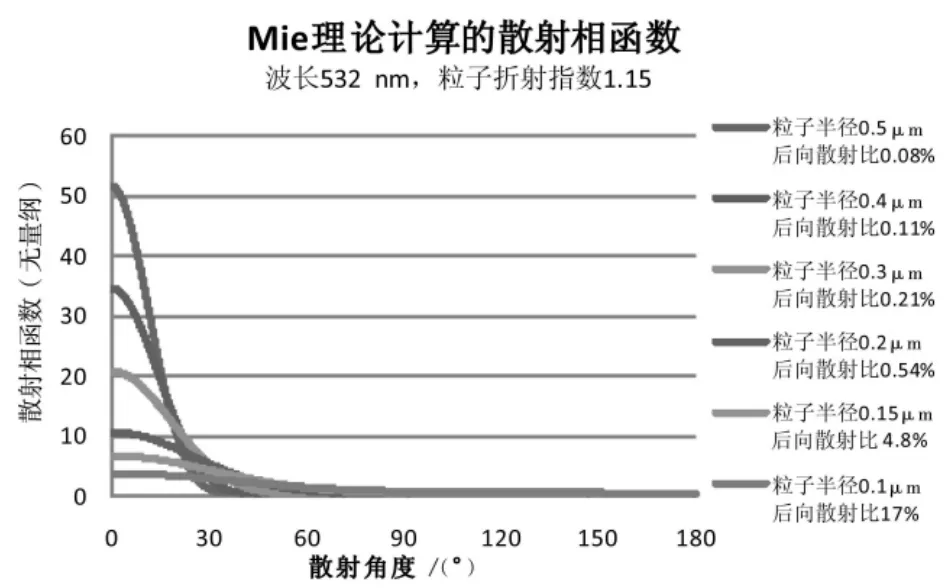
图5 Mie理论模拟的粒子散射相函数

图5的图例标识了不同模拟情形下的粒子半径及计算的后向散射比。从图中可以看出，在模拟波长、介质折射指数、粒子折射指数固定的情况下，随着粒子半径的减小，粒子的后向散射比逐渐增大。在粒子半径（0.5 μm）与波长相当时，后向散射比仅为0.08%，而粒子半径减小到0.1 μm时，后向散射比增加到17%，增长迅速。当粒子半径继续减小时，后向散射比将继续增加。另外，粒子折射指数在1.15～1.2间变化和介质折射指数轻微变化时，上述变化规律依然适用。

由此可见，虽然实际计算的后向散射比与Mobley[3]给出的典型海水Bp值在0.005～0.03之间的结论差别较大，但通过理论模拟证明，本文给出的反演结果是合理可信的。这也充分说明了该区域的水体属于典型的具有强后向散射特征的II类水体。图6给出了2号断面粒子后向散射比例的垂直分布图。

从图中可以看出，粒子后向散射比例靠近陆地或岛屿的区域较大，而在远离陆地的区域较小。这可能是陆源输入的粒子引起的，也可能是海底悬浮物质再悬浮引起的。

根据（5）式和（6）式，表4给出了根据衰减系数斜率得到的粒子尺度分布斜率ξC。

从表4可以看出，粒子尺度分布斜率ξ的最小值已经超出了4.5，即超出了（7）式的适用范围。因此，本文利用另外一种方法计算折射指数，并获得散射相函数。

图6 2号断面粒子后向散射比例的垂直分布，其中右图为断面站位示意图

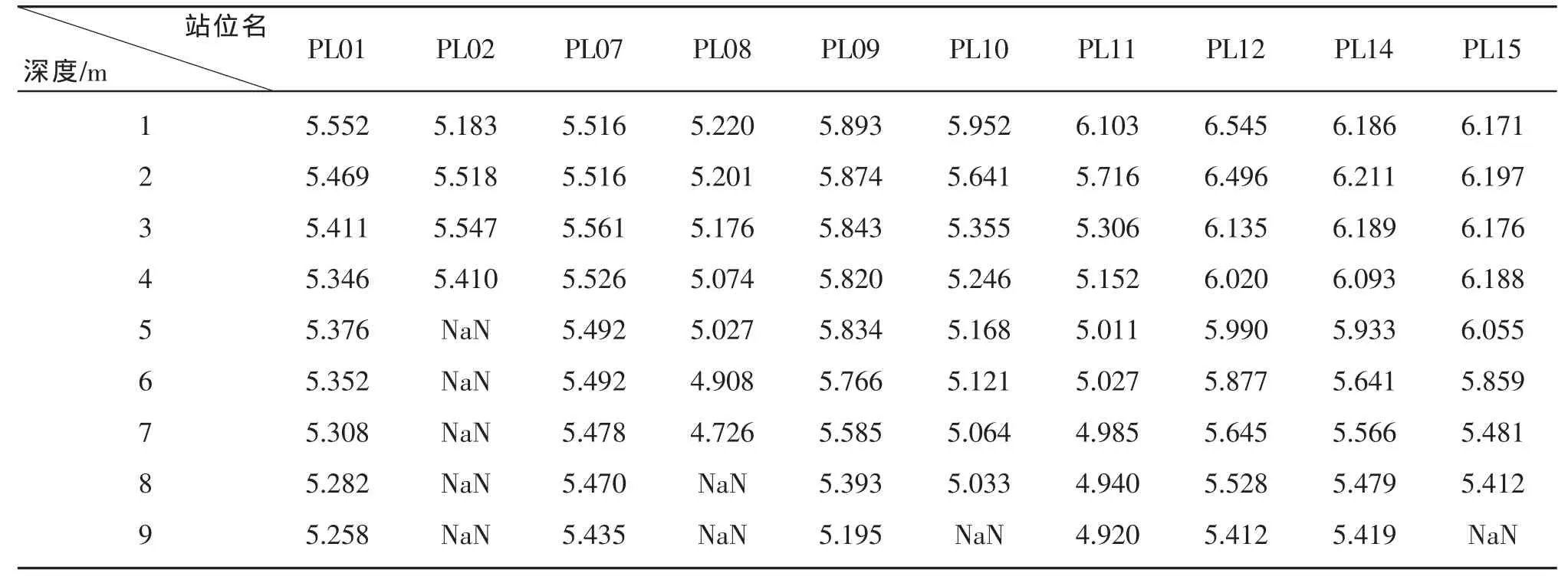
表4 根据（5）式计算得到的各站位不同水层的粒子尺度分布斜率ξC

根据（9）式和（10）或（11）式可以确定组合（np，ξ）。表5给出了粒子折射指数np。

从表5可以看出，对于绝大多数站位，表层水体的粒子折射指数np要略低，而随水深增加np逐渐增加，只有PL08站位（离岸最近）的np最大值出现在中间水层（3～5 m）；而对比各站位间的差异，np均大于1.15，尤其是PL08，PL09和PL10站位的np明显高于其他站位。根据Mobley[3]，该海域的粒子应属于折射指数在1.15量级的矿物颗粒。图7给出了2号断面粒子折射指数的垂直分布图。

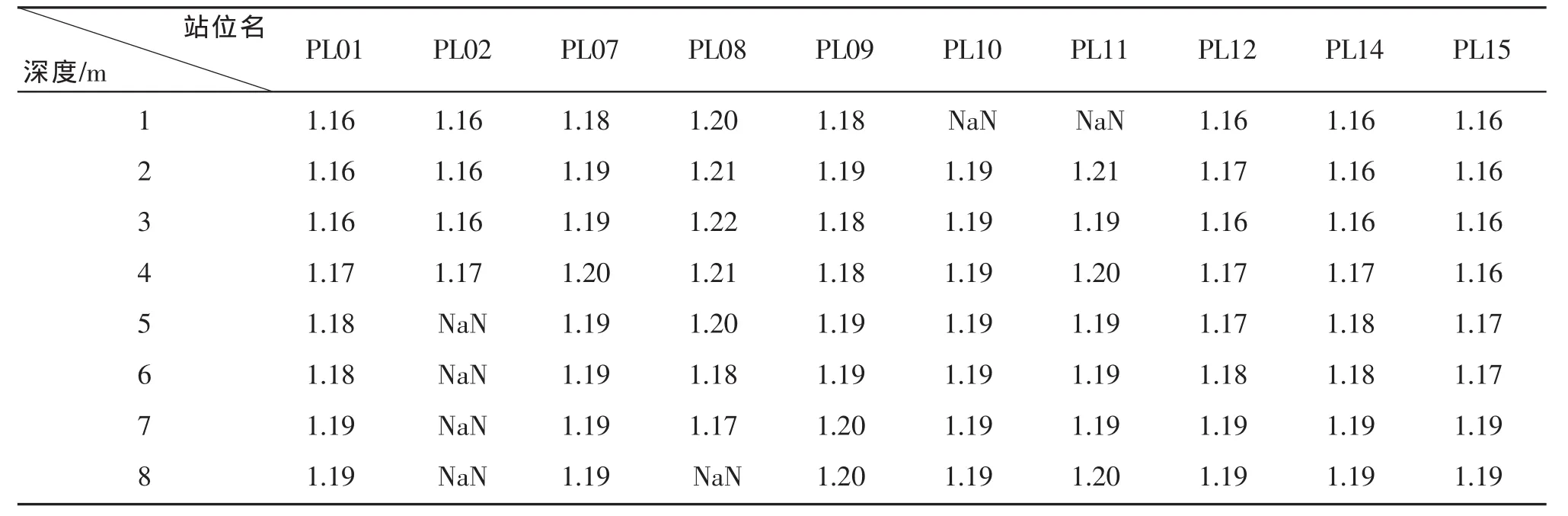
表5 各站位不同水层的粒子折射指数np

从图中可以看出，np的分布规律性较差，无论是不同站位还是不同深度，np均存在忽大忽小的现象。离岸最远的区域，np最小。因此，np的分析需要在今后的研究中更加细化和有针对性。表6给出了粒子尺度分布斜率ξ。

图7 2号断面粒子折射指数的垂直分布，其中右图为断面站位示意图

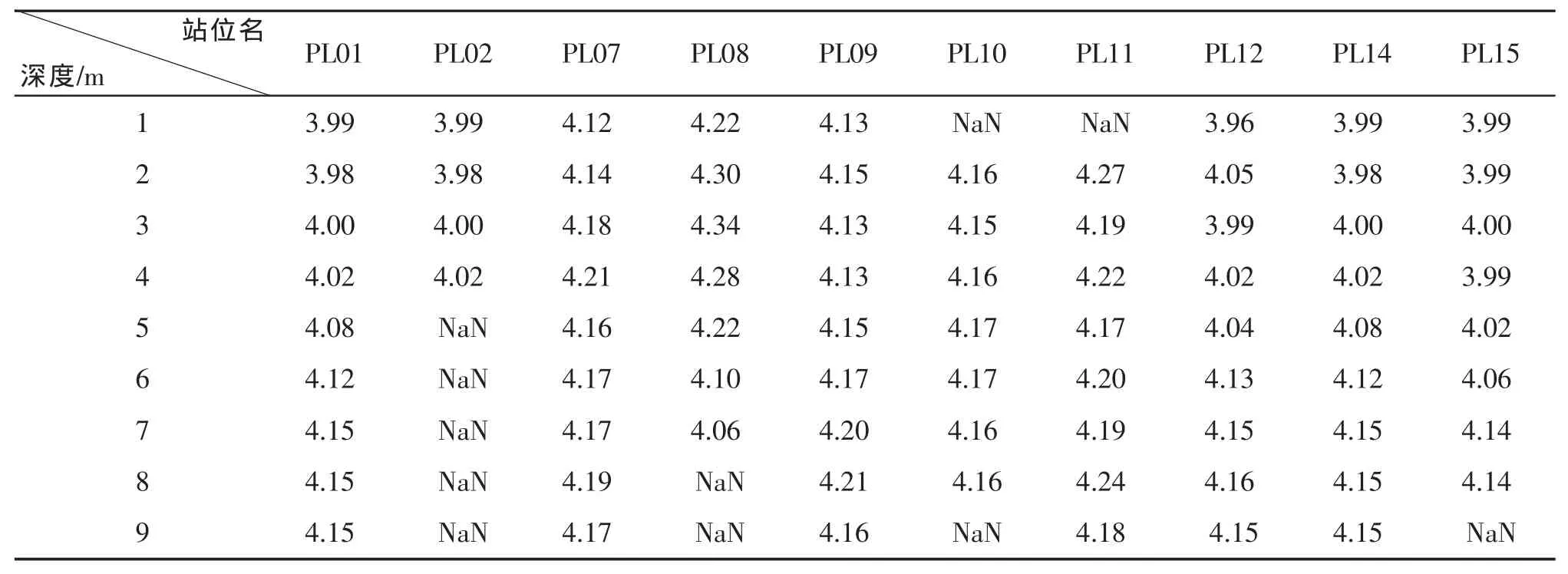
表6 各站位不同水层的粒子尺度分布斜率ξ

从表6可以看出，不同站位不同水层的ξ均大于3.9。对于绝大多数站位，表层水体的粒子尺度分布斜率ξ要略低，而随水深增加ξ逐渐增加，只有PL08站位（离岸最近）的ξ最大值出现在中间水层（3～5 m）；而对比各站位间的差异，PL07，PL08，PL09，PL10和PL11显著高于其他站位，这说明这些站位的平均粒子尺度要比其他站位小，按照散射理论，其散射要强于其它站位，这也能更好的佐证表3的结论。然而，需要对该区域海水中的粒子进行进一步研究，以便更好地了解该区域的粒子尺度分布情况。

3 结论

本文应用水体光学散射理论基础，分析了水体散射特性数据的应用方法，并将其应用到烟台蓬莱附近的试验数据，取得了较好的效果。利用ACS衰减系数获取的粒子尺度分布斜率ξ超出了（7）式的应用范围，因此采用（9）式和（10）或（11）式获取粒子折射指数np和粒子尺度分布斜率ξ。从分析结果可以看出，烟台蓬莱附近海域水体散射占据主导，且后向散射比例超过了Mobley给出的0.03的上限，属于具有强后向散射特征的II类水体。经过Mie模拟计算，在粒子半径为0.1 μm时，粒子的后向散射比达到了17%，证明了本文结果的合理性。不过，由于水体散射特性受到粒子尺度、折射指数等诸多要素的影响，本文仅对试验数据进行了初步分析，未对造成该海域散射特性分布差异的原因做进一步分析，仍有待进一步研究。

[1]FARGIONGS,MUELLER J L.Ocean optics protocols for satellite ocean color sensor validation,Revision 3[R].NASA/TM-2002-21004,2002.

[2]CDMobley.Light and Water：Radiative Transfer in Natural Waters[M].Academic,San Diego,Academic Press，1994.

[3]Curtis DMobley,Lydia KSundman,Emmanuel Boss.Phase function effects on oceanic light fields[J].Appl Opt，2002,41：1035-1050.

[4]Twardowski MS,Boss E,Macdonald JB.Model for estimating bulk refractive index from the optical backscattering ratio and the implications for understandingparticle composition in case I and case II waters[J].Journal ofGeophysical Research,2001,106(C7)：14129-14142.

[5]JerlovNG.Marine Optics[M].NewYork：Elsevier scientific Pulishingcompany,1976：1035-1050.

[6]李铜基，陈清莲，杨安安，等.黄东海春季水体后向散射系数的经验模型研究[J].海洋技术，2004,23(3)：10-14.

[7]宋庆君，唐军武.黄海、东海海区水体散射特性研究[J].海洋学报，2006,28(4)：56-63.

[8]崔廷伟，张杰，马毅，等.渤海近岸水体后向散射系数反演模型[J].光学学报，2008，28（11）：11.

[9]周雯，曹文熙，李彩.海水中矿物质颗粒吸收和散射特性Mie理论分析[J].热带海洋学报，2008，27（1）：1.

[10]马荣华，宋庆君，李国砚，等.太湖水体的后向散射概率[J].湖泊科学，2008,20(3)：375-379.

[11]Petzold,Theodore J.Volume ScatteringFunctions for Selected Ocean Waters[M].San Diego：Scripps Institution ofOceanography,1972.

[12]LCHenyey，J LGreenstein.Diffuse radiation in the galaxy[J].Astrophys J,1941，33：70-83.

[13]GWKattawar.Athree-parameter analytic phase function for multiple scatteringcalculations[J].J Quant Spectr.Radiat.Transfer.1975，15：839-849.

[14]V I Haltrin.Exact solution of the chatacteristic equation for transfer in th eanistropically scattering and absorbing medium[J].Appl Optics,1988,27（3）：599-602.

[15]W M Cornette，J G Shanks.Physically reasonable analytic expression for the single-scattering phase function[J].Appl Optics,1992，31（16）：3152-3160.

[16]LOReynolds，NJ McCormick.Approximate two-parameter phase function for light scattering[J].J Opt Soc Amer,1980，70：1206-1212.

[17]VI Haltrin.Theoretical and empirical phase functions for Monte Carlocalculations oflight scatteringin seawater[C]//Proceedings ofthe Fourth International Conference Remote Sensingfor Marine and Coastal Environments：Technologyand Applications,Envir.Res.Inst.Of Michigan(ERIM),Ann Arbor,MI,1997,I：509-518.

[18]GR Fournier，J LForand.Analytic phase function for ocean water,SPIE[M].Ocean Optics XII,J SJaffe,ed,1994，2258：194-201.

[19]苏丽萍，任德明，曲彦臣，等.海水中悬浮粒子归一化体散射函数的研究[J].激光杂志.2006,27(5)：65-66.

[20]詹海刚,施平,陈楚群，等.基于贝叶斯反演理论的海水固有光学特性准分析算法[J].科学通报,2006,51(2)：204-210.

[21]Boss E,MSTwardowski，S Herring.The shape ofthe particulate beamattenuation spectrumand its relation tothe size distribution ofoceanic particles[J].Applied Optics,2001，40：4885-4893.

[22]Boss E,WS Pegau,WDGardner,et al.The spectral particulate attenuation and particle size distribution in the bottomboundarylayer of a continental shelf[J].Journal ofGeophysical Research,2001：9509-9516.

[23]Diehl P,H Haardt.Measurement of the spectral attenuation to support biological research in a “plankton tube”experiment Oceanol.Acta,1980，3：89-96.

[24]G Fournier，MJonasz.Computer-based underwater imaging analysis in Airborne and In-water Underwater Imaging,G.Gilbert,ed.,Proc.SPIE 3761,1999：62-77.

Preliminary Research on Scattering Properties of Penglai Offshore Seawater

HAN Bing,LI Tong-ji,ZHU Jian-hua
（National Ocean Technology Center,Tianjin 300112， China）

Suitable methods are selected to analyze scattering properties and then verified using experimental data obtained from seawater near Penglai.As can be seen,scattering dominates in water attenuation with single scattering albedo (ω0)varying between 0.6 and 0.8.Also,the fact that backscatter ratio(Bp)varies between 0.08 and 0.17,which is much higher than 0.03 given by Mobley(2002),indicates high backscattering characteristic of seawater of typical Type II water.However,the result is consistent with simulation based on Mie theory.Particle refractive index (np),higher than 1.15,indicates the characteristic of mineral compared to that of living microorganism between 1.01 and 1.09.The field experiments show that such methods as listed here are feasible,which could provide reference for studying the scattering properties of China’s offshore seawater.

water scattering;refractive index;backscattering ratio;single scattering albedo;Penglai

P7；TP7

B

1003-2029（2011）04-0074-08

2011-05-20

国家海洋局青年海洋科学基金资助项目—体散射特性精确测量与分析技术研究（2010414）

韩冰（1980-），男，大学本科，工程师，研究方向为水色遥感机理与应用。Email：hotrice@sina.com

*本文提到的粒子折射指数均指相对子水的相对折射指数