一种特殊零件的数控编程与加工
2011-01-07伍小建
伍小建
(广东省梅州市高级技工学校,广东 梅州514071)
在某市举行的数控车工技能竞赛中,有一个特殊零件(如图1)需要加工(采用手工编程)。
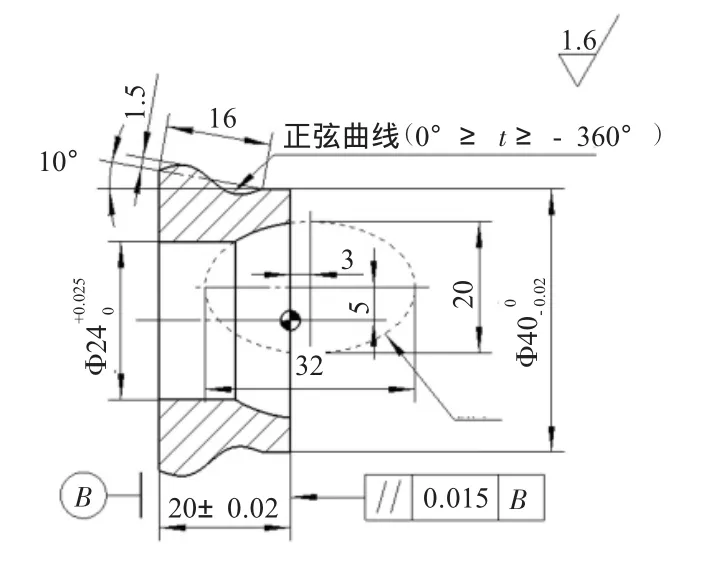
图1 技能竞赛中特殊零件
加工这个零件有一定的难度,主要有如下问题需要解决:
(1)确定加工工艺;
(2)旋转正弦曲线如何编程;
(3)保证总长尺寸精度及平行度。
1 加工工艺
比赛现场提供的毛坯中有一根为Φ50 mm×100 mm的45钢棒料,供图1零件与另一个长度为72 mm的零件合用。从结构、精度、效率和现场条件等方面考虑,图1零件不宜采取车好一头后调头装夹车另一头的方法,故采取如下加工工艺:
(1)用三爪卡盘夹Φ50 mm×100 mm的棒料,伸出长度为28~30 mm;
(2)用Φ22 mm的麻花钻钻孔;
(3)车外圆(正弦曲线)及右端面;
(4)车内孔;
(5)用内尖刀在总长20 mm末端预先车出内倒角;
(6)把工件切断,保证总长(20±0.02)mm及平行度。
2 旋转正弦曲线的编程
2.1 非圆曲线手工编程难点的原因
非圆曲线用CAM软件进行自动编程相对简单一些,但在绝大多数情况下,数控车床主要还是依靠手工编程。非圆曲线的手工编程,是数控编程中的难点,主要原因有:
(1)数控系统本身不存在加工非圆曲线的指令,要用许多微小的直线段来逼近非圆曲线轮廓,要编制宏程序,要熟悉数学计算,使用循环语句或条件转移语句等,进行变量编程。
(2)要熟悉参数变化及其相互关系。程序中的参数如选取不当,很容易产生过切或欠切等现象,甚至造成工件报废。
(3)为了保证加工精度,精车需要选取较小的步距,并进行刀尖圆弧半径补偿。但步距过小(即线段过短),又无法进行半径补偿;步距过大,则拟合误差过大;而加工中能够执行的最小步距,又与刀尖圆弧半径的大小有关。因此要根据实际情况合理选取步距。
2.2 旋转正弦曲线编程难的原因
如果非圆曲线的轴线与数控车床Z轴(或X轴)平行(如本零件中的32 mm×20 mm椭圆),则难度还不是很大,这里就不再叙述。而本零件中的正弦曲线轴线与数控车床Z轴呈一定夹角(即旋转了一个角度),编程难度大大增加,原因除了上述几点之外,还有下列两点:
(1)常用的车床数控系统没有坐标旋转指令。
(2)非圆曲线旋转后数学计算更加复杂。
2.3 计算和编程方法
如图2,先以本零件正弦曲线起点O1为原点建立一个直角坐标系X'O1Z',坐标系的O1Z'与正弦曲线的轴线重合。

图2 旋转正弦曲线的坐标
正弦曲线参数为t,起点t为零。正弦曲线上任一点 P到 O1X′的距离为 B'P,到 O1Z'的距离为A'P。根据正弦曲线的参数方程,P在X′O1Z'坐标系中坐标值的计算公式为
X'=A'P=O1B'=1.5 sin t
Z'=B'P=O1A'=16 t/360°
(t为0°~-360°范围内的任一角度)
再以O1为原点建立一个与数控车床坐标系平行的坐标系X1O1Z1,该坐标系相当于X'O1Z′坐标系绕原点O1逆时针旋转10°。正弦曲线中任一点P到O1X1的距离为BP,到O1Z1的距离为AP,P在X1O1Z1坐标系中坐标值的计算公式为
X1=O1B=AP=AD+DP=CA'+DP
=O1A'sin(-10°)+A'P cos(-10°)
=Z'sin(-10°)+X'cos(-10°)
=16 t/360°sin(-10°)+1.5 sin t cos(-10°)
Z1=BP=O1A=O1C-AC=O1C-DA'
=O1A'cos(-10°)-A'P sin(-10°)
=Z'cos(-10°)-X'sin(-10°)
=16 t/360°cos(-10°)-1.5 sin t sin(-10°)
而数控加工时,以工件右端面中心点为原点,由图1可知,正弦曲线起点O1在工件坐标系中的坐标值为
X=40(直径编程)
Z=16 cos(-10°)-20
=-4.243
故正弦曲线上任一点在工件坐标系中的坐标值为
X=2 X1+40(直径编程)
=2[16 t/360°sin(-10°)+1.5sin t
cos(-10°)]+40
Z=Z1-4.243
=16 t/360°cos(-10°)-1.5 sin t sin(-10°)
-4.243
根据上述计算,编制旋转正弦曲线的加工程序如下(FANUC 0i系统):
O0011;(程序号)
T0202 G00 X100 Z100;(选择2号刀,即外圆尖刀VBMT160404 HQTN60,快速定位在X100 Z100处)
M03 S900;(主轴正转,900 r/min)
M08;(冷却液开)
G00 X52 Z2;(刀具快进至 X52 Z2处)
G73 U5.5 W0 R5;(用G73指令进行粗车循环)
G73 P1 Q3 U0.8 F0.12;(粗加工 N1—N3段程序,X方向留精车余量0.8 mm)
N1 G00 X40;(轮廓第一段程序)
G01 Z-3.5 F0.08;(直线插补至Z-3.5处)
#1=0(变量#1赋初值0,即起点处t=0°)
N2#2=1.5*SIN[#1];[变量#2为正弦曲线在坐标系X'O1Z'中的X'值(半径)]
#3=16*#1/360;(变量#3为正弦曲线在坐标系X'O1Z'中的 Z'值)
#4=#3*SIN[-10]+#2*COS[-10];[变量 #4 为正弦曲线在坐标系X1O1Z1中的X1值(半径)]
#5=#3*COS[-10]-#2*SIN[-10];(变量 #5 为正弦曲线在坐标系X1O1Z1中的Z1值)
#6=2*#4+40;[变量#6为正弦曲线在工件坐标系中的X值(直径)]
#7=#5-4.243;(变量#7为正弦曲线在工件坐标系中的Z值)
G01 X#6 Z#7 F0.08;(直线插补至 X#6 Z#7 处,用微小直线段逼近正弦曲线进行加工)
#1=#1-1.8;(#1步距为1.8,即正弦曲线参数t值每循环一次减少1.8°)
IF[#1 GE-360]GOTO 2;(如果#1≥ -360时,则返回N2程序段,继续循环;否则执行后面程序段)
G01 W-4;(车切断部位外圆)
N3 G00 X50;(轮廓最后一段程序)
G00 X55 Z5;(快速退刀至 X55 Z5处)
S1500;(主轴转速 1500r/min)
G42 G00 X52 Z2;(刀具快进至X52 Z2处,并用G42指令进行刀尖圆弧半径补偿)
G70 P1 Q3;(用G70指令精车N1—N3段程序确定的轮廓)
G40 G00 X100 Z100;(快速退刀至 X100 Z 100处,并用G40指令取消刀尖圆弧半径补偿)
M30;(程序结束)
外圆刀VBMT160404 HQ TN60的刀尖圆弧半径为R0.4,在采用刀尖圆弧半径补偿的情况下,正弦曲线参数变量#1的步距取1.8,能保证比较高的拟合精度。
数控系统的G73等粗车循环指令不执行G41、G42刀尖圆弧半径补偿(G70精车指令才执行),故程序中精车余量不能过小,以免粗车过切而造成精车时正弦曲线与外圆刀副偏角对应的一侧无加工余量。这里余量取0.8 mm是比较合适的。
3 切断取总长及防碰伤
这个零件本身没有合适的装夹部位,且零件两端面平行度公差为0.015 mm,在没有软卡爪或专用夹具的情况下,不宜采取车好一头后调头装夹车另一头的方法,所以采取切断时取总长的工艺,既保证精度,又提高效率。但本零件的总长公差为0.04 mm,要求比较高,切断刀Z轴方向的对刀和切断程序的编制至关重要。由于取总长是通过切断刀右刀位点的切削来保证的,为了减小对刀和测量误差,并避免Z轴反向间隙的影响,采取如下方法:
选取刀宽3 mm、刃口锋利的切断刀,准备一个平面度较好(有一面即可)的垫块。对刀时,一手将垫块平面度较好的一面压在工件右端面上,一手摇操作面板手轮,使切断刀从Z轴的负方向往正方向移动(消除反向间隙),右刀尖轻轻碰到垫块左端面即停止(如图3)。刀具在Z轴方向不动,在刀偏中输入“Z0”,按“测量”按钮,即完成切断刀Z轴方向的精确对刀。
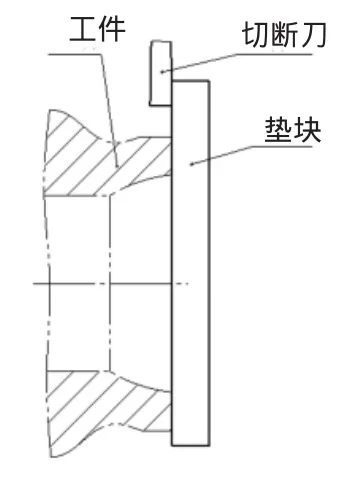
图3 对刀方法
切断编程如下:
O0012;(程序号)
T0303 G00 X100 Z100;(选择3号刀,即切断刀,以右刀尖为刀位点,快速定位)
M03 S700;(主轴正转,700 r/min)
M08;(冷却液开)
G00 X50 Z-20.5;(刀具快速移动至X50 Z-20.5处)
Z-20;(刀具从Z-20.5往Z-20移动,消除反向间隙)
G01 X23 F0.04;(切断)
G00 X50;(快速退刀至 X50处)
X100 Z100;(快速退刀至 X100 Z100处)
M30;(程序结束)
程序中消除反向间隙很重要,刀具到达切断位置前要从Z轴的负方向往正方向移动(与对刀时的状况一致)。
上述方法能保证工件比较高的总长尺寸精度及两端面平行度。
还要预防工件切断后掉下来碰伤。一般情况下可事先在工件下方准备一个塑料桶,或其他比较柔软的盛具,工件落在其中就不会碰伤。
如果上述方法不便实施,还可采取如下措施:
(1)对于空心工件,可用一根较长的塑料棒或木棒等插入工件空心处,工件切断后主轴立即停转(刀具先不要退出),工件被挂住就不会掉下来。
(2)对于实心工件,切断刀切到工件断口直径还剩下Φ2.5 mm左右即停止进给,主轴停转(刀具先不要退出,以免划伤工件端面),然后用手工把工件折断。如果断口直径切得太小,则在进给力、切削力和工件本身重力的作用下自动断裂,如果断口直径切得太大,则手工难以折断。
4 结束语
通过上述编程和加工方法,保证了旋转正弦曲线的形状精度,保证了总长尺寸精度和平行度,提高了生产效率,同时避免了工件碰伤现象。
[1]冯志刚.数控宏程序编程方法、技巧与实例[M].北京:机械工业出版社,2007.
