不确定性机器人的神经网络自适应控制

周景雷

（菏泽学院机电工程系，菏泽274015）

不确定性机器人的神经网络自适应控制

周景雷

（菏泽学院机电工程系，菏泽274015）

针对一类不确定性机器人轨迹跟踪问题，提出了一种神经网络自适应控制。首先利用反馈控制技术把基于拉格朗日方程的多关节机器人动力学模型转化成二阶系统。其次，将神经网络自适应控制方法和所转化的二阶系统相结合，找到了一种新方法来研究机器人系统，该方法是应用RBF神经网络自适应控制思想来设计控制器，所设计的控制器能够保证机器人的实际运动轨迹渐近无误差地跟踪给定的期望轨迹。最后，以两关节机器人系统为例，给出其仿真试验结果。

不确定性；机器人；神经网络；自适应控制；渐近稳定

机器人系统是一类时变、强耦合和高度非线性的动力学系统，并且存在着大量的不确定性因素，因而想获得机器人的精确数学模型是不可能的。

近些年来基于机器人的智能控制受到控制领域的广泛关注，提出了很多非线性补偿控制方法［1－4］。文献［3］采用了自适应控制方法，能够通过在线估计未知参数，并且根据其估计值修正控制策略，然而其设计的控制器有着变结构的形式，这样必然会存在"抖振"现象。文献［4］采用了神经网络控制，虽然在逼近区域内利用神经网络其到了补偿作用，能够克服变结构的“抖振”，但最大的问题是如何得到准确的在线训练数据和怎样解决实时控制差的问题。这两种智能控制都有着一定的问题，于是人们开始将自适应控制和神经网络控制结合起来［5－6］。文献［5］将这种结合应用到了空间机器人上，这不具有一般性；文献［6］在自适应控制和神经网络控制的基础上又增加了迭代学习控制，这虽然有助于提高控制的精度和稳定性，但是这必然增加了难度，不宜操作。同时，上述文献均未将基于拉格朗日方程的机器人动力学模型，转化成一个比较简单的、易于控制的模型。

考虑到上述不足之处，本文提出一种神经网络自适应控制，将其直接应用到带有外界干扰的不确定机器人系统当中去。首先将基于拉格朗日方程的机器人动力学模型转化成二阶系统，这是一状态空间模型，于是可以利用现代控制理论对其进行控制。

然后，采用了神经网络自适应控制方案，通过李雅普诺夫稳定性分析设计了控制器和自适应调整律，很好地保证了实际运动轨迹渐近无误差地跟踪给定的期望轨迹。

1 机器人系统描述

基于拉格朗日方程的n关节机器人动力学模型可由下面二阶非线性向量微分方程来描述

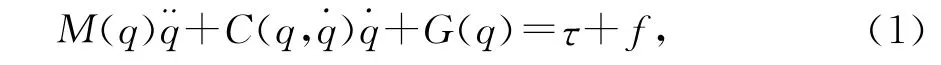
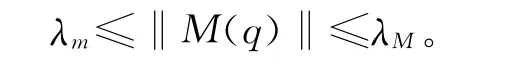
对于外界不确定性干扰需要满足假设：假设外界不确定性干扰f有界。

令

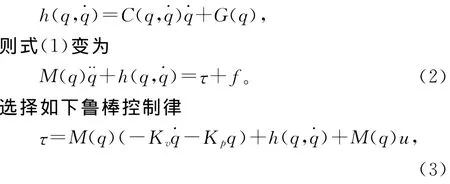
式（3）中，Kv，Kp为选定的正定增益阵，分别可理解为微分和比例增益。为简便起见，下文设它们都为对角阵。

由式（2）～（3）得到系统误差动态方程

如果再令d＝M－1（q）f，则得到更简单的状态方程

上式中，u为外界控制输入量，d包含了外界不确定性干扰。再令x＝［］T，x1＝q，x2＝˙q，则机器人系统就可以写成

式（4）中，f（x）＝－Kv˙q－Kpq，假设其未知，因为我们是不知道实际运动轨迹的，目的就是控制实际轨迹跟踪给定的期望轨迹qb，所以这样的假设是可以的。根据d＝M－1（q）f中M（q）的有界性和对外界干扰f所做的假设知，有‖d‖≤d0，d0为已知的正常数。

我们再定义跟踪误差e＝q－qd，显然，qd二阶连续可导。那么对于系统（4）的控制目的，就是设计外界控制输入u，使实际轨迹qd渐近地跟踪给定期望轨迹e，也即跟踪误差e趋于零。

2 神经网络自适应控制器

2.1 神经网络估计

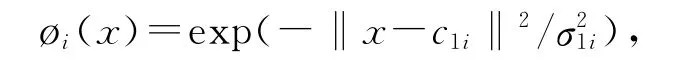
上式中，cji∈R2n和σji（j＝1，2）分别表示第i个基函数的中心向量和宽度。cji和σji是可调的参数，在实际工程应用上，为了数学上处理方便，可以根据对象的一些信息，将它们的取值固定，不过有时也利用局部训练技术来获取它们的值［7］。

下面给出2个假设。

这里要注意：（A1）所说的是神经网络估计误差的能力，已经证明了只要加权矩阵也就是神经元的个数足够多，那么网络估计误差会变得任意小［8］。

我们采用径向基（RBF）神经网络来估计未知函数 ，其估计＾f（x）为

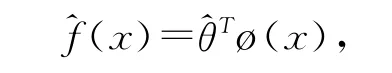
这里＾θ是网络加权矩阵θ的估计。下面我们要设计网络加权的自适应修正律来保证这种网络性能的一定要求。向量ø（x）是高斯型函数，其第i个元素分别有如下数学表示形式

2.2 控制器设计

为了下面的需要，我们在这里先定义一个开关函数

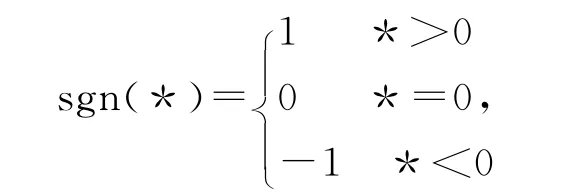
其中，星号表示一个任意的标量。

再给出一个引理：设a，c∈Rn为列向量，D∈Rn×n为方阵，则有a′Dc＝tr（D′ac′）。

对于系统（4），我们选取如下控制律

式（5）中，

随着大数据的广泛应用和新技术的层出不穷，智慧城市建设得到有序推进，创新融合理念深入人心。作为公共文化服务机构，图书馆如何在自动化、数字化、智能化的基础上，顺应时代发展要求，开展图书馆智慧化建设；如何以读者需求为导向，建立智慧化的信息系统，提高馆员工作效率和资源利用率，是当前我们图书馆人应该思考的课题。新一代智慧图书馆信息系统的建设面临着诸多不确定性，比如技术进步、社会环境变化等，但可以确定的是，智慧化、复合型是新一代智慧图书馆信息系统的重要特征，也是图书馆转型与超越的必然要求。

这里，α，β∈Rn×n为正定增益矩阵，在一般情况下为了解耦方便，都取它们为对角阵。sgn（e1）为一列向量，其中的每一个元素sgni（e1i）都满足上面定义的开关函数。e1为定义的滤波误差［9］，有e1＝［P2P3］S，S＝［eT˙eT］T。［P2P3］为下面李雅普诺夫方程（9）的解P的一部分

把式（5）～（7）代入式（4），得误差状态方程

式（8）中

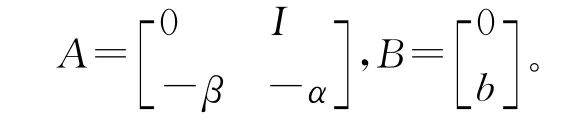
其中

矩阵A是稳定矩阵［10］，于是，对于下面的李雅普诺夫方程，总存在正定解P

选择如下的权矩阵修正算法

式（9）中，η为正常数，作为自适应律。很容易得出下面的结论：考虑系统（4）和上述所做的假设，如果控制器由式（5）～（6）组成，权矩阵由式（10）来调节，那么跟踪误差e渐近收敛到0点。

证明，我们构造如下李雅普诺夫函数

进一步，把修正法则（10）带入上式并根据引理得

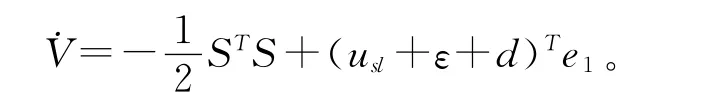
根据式（7）以及（A1）和对d所做的有界性的限定，容易证明下面的不等式成立

对于第i个分量，设e1i＞0，有

同理，当e1i＝0，不等式（11）仍然成立。并容易得知，当e1i＝0，不等式（11）变成了等式。因此，不等式（11）总是成立的，于是

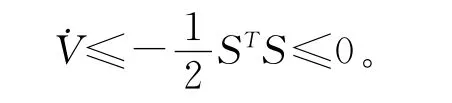
这样我们就证明了李雅普诺夫函数 是单调递减的，那么就可以得出闭环系统是全局渐近稳定的，也就是当t→∞有S→0，那么跟踪误差e和它的导数˙e也都渐近收敛于0。

3 举例仿真

下面以两关节机器人为例来验证我们的控制方法，这种机器人机械臂的结构图及参数：连杆质量m1，m2（kg）连杆长度l1，l2（m）角坐标q1，q2（rad）如图1所示。

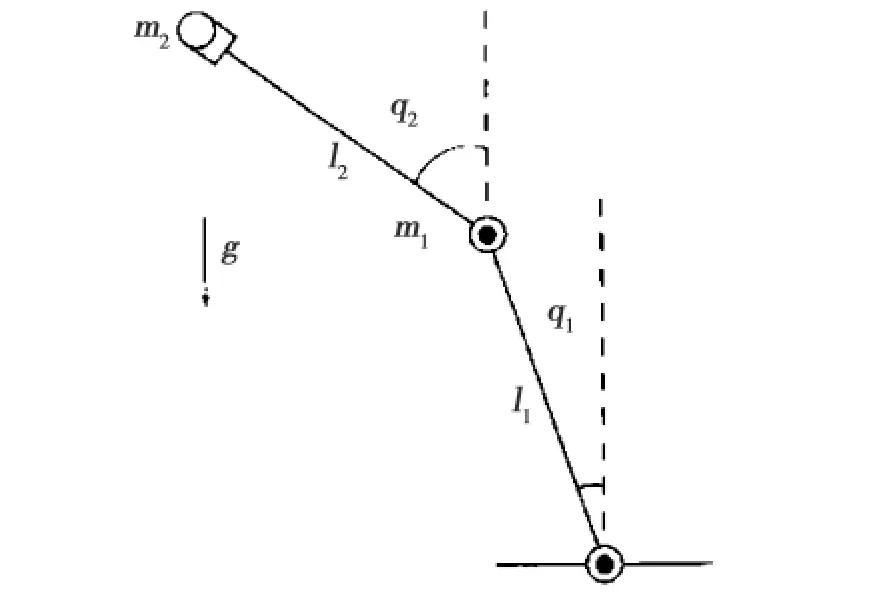
图1 两关节机器人Fig.1 The t wo－link robot

动力学模型（1）中的参数为

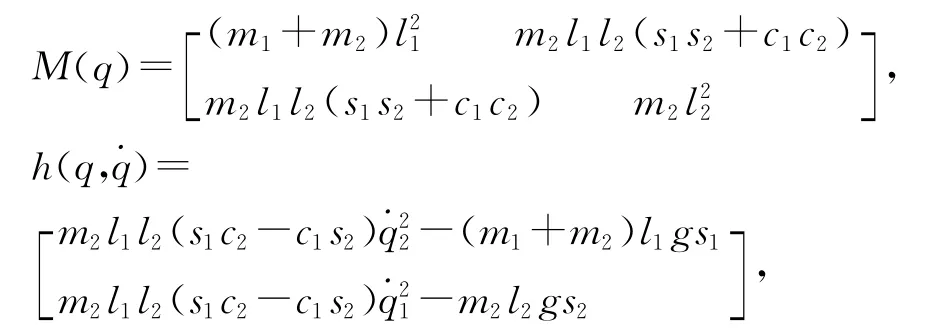
这里q＝［q1，q2］T，ci＝cos（qi），si＝sin（qi），i＝1，2。

为了仿真简便，我们简单的取各参数值如下m1＝1（kg），m2＝10（kg），l1＝l2＝1（m），初始坐标选为q1（0）＝q2（0）＝－0.5，˙q1（0）＝˙q2（0）＝0，外界干扰f＝［0.5cos（t） 0.5sin（t）］T，期望轨迹qd1＝0.5cos t，qd2＝0.5sin t，a0＝4I2，a1＝2I2。

选择2×20×1的RBF神经网络来估计f（x）＝－Kv˙q－Kpq，Kq，Kv＝Kp＝I2。选取加权矩阵的初值为＾θ（0），宽度σ＝0.2，中心ci在（－0.2，0.2）任意选择。仿真图如图2所示。图2中，点划线表示的是实际轨迹，实线表示期望轨迹。从仿真图中，我们可以看出，经过很短的时间，实际轨迹就与期望轨迹重合了，这说明我们的理论可行。

图2 轨迹曲线Fig.2 Track curve

4 小结

本文根据状态空间中的李雅普诺夫思想来设计权矩阵修正律和控制器，对机器人系统的神经网络自适应控制器进了研究，其思路清晰，设计简单。所设计的控制器很好地保证了机器人系统的稳定性，使机器人的实际运动轨迹渐近无误差地跟踪给定的期望轨迹。

［1］Ham C，Qu Z，Johnson R.Robust f uzzy control for robot manipulators［J］.IEE Peoceedings on Control Theory and Application，2000，147（2）：212－216.

［2］Jin M L，Lee J，Chang P H，et al.Practical nonsingular ter minal sliding－mode control of robot manipulators for high－accuracy tracking control［J］.IEEE Transactions on Industrial E－lectronics，2009，56（9）：3593－3601.

［3］Su H H，Li C F.A fully adaptive decentralized control of robot manipulators［J］.Automatica，2006，42（5）：1761－1767.

［4］张文辉，齐乃明，尹洪亮.不确定机器人的神经网络轨迹控制［J］.自动化与仪表，2010，30（5）：22－25.

［5］谢箭，刘国良，颜世佐，等.基于神经网络的不确定性空间机器人自适应控制方法研究［J］.宇航学报，2010，31（1）：123－129.

［6］王跃灵，沈书坤，王洪斌.不确定机器人的自适应神经网络迭代学习控制［J］.武汉理工大学学报，2009，31（24）：135－139.

［7］Sanner R M，Sloting J J E.Gaussian net wor ks for direct adaptive control［J］.IEEE Transactions on Neural，Networ ks，1992，3（6）：837－863.

［8］Chen B S，Lee T S，Feng J H.A nonlinear H∞control design in robotic systems under parameter perturbation and external disturbance［J］.International Journal of Control，1994，59（2）：439－461.

［9］Niu Y G，Zou Y，Yang C W.Neural net work－based adaptive tracking control for a class of nonlinear systems［J］.Control Theory and Applications，2001，18（3）：461－464.

［10］周景雷，张维海.一种机器人轨迹的鲁棒跟踪控制［J］.控制工程，2007，14（3）：336－339.

Adaptive Control for Uncertain Robot Based on Neural Net work

ZHOU Jinglei
（Department of Machine and Electronic，Heze College，Heze 274015，China）

A kind of neural net work adaptive control for a sort of uncertain robotic system is presented.First，the multi－joint robotic dynamical model based on the lagrange equation istransf or med into a two－order system via feedback control technique.Then，combine the two－order system with the neural net work adaptive control，finding out a new way to study the robotic systems.This way is to use the RBF neural net work adaptive control methods to design the controller，which can guarantee the actual tracks of robot asymptotically tail after the given desired tracks without any error.At last，take a two－joint robot as an example and give its simulation results.

uncertain；robot；neural net work；adaptive control；asymptotically stable

TP242

A

1007－7383（2011）03－0390－04

2011－01－23

山东省自然科学基金项目（ZR2009GZ001）

周景雷（1981－），男，硕士，研究方向为机器人控制、鲁棒控制。