非局域铅玻璃介质中偶极稳态孤子解探究
2011-01-05曹雅平黄春福
曹雅平,黄春福
(天津师范大学 物理与电子信息学院,天津 300387)
非局域铅玻璃介质中偶极稳态孤子解探究
曹雅平,黄春福
(天津师范大学 物理与电子信息学院,天津 300387)
在无限非局域铅玻璃介质中,假设(1+1)维偶极孤子的试探解为具有普遍意义的带传播常数项exp(iλZ)形式的波函数,利用变分法得到描述偶极孤子稳态解的一般参数耦合方程;推导出孤子振幅平方(B2)与束宽六次方(W6)的乘积为一定值,且振幅B随束宽W的增大而减小;得到传播常数与孤子功率和介质宽度的关系式,说明传播常数是表示功率大小的参量,同时还是介质宽度的函数.最终,通过数值模拟验证了变分计算的结果,观察到(1+1)维偶极光束在该参数方程的制约下都能形成偶极孤子并稳定传输.
非线性光学;偶极孤子解;铅玻璃;变分法;传播常数
当由介质非线性引起的自聚焦效应与光束本身的衍射效应达到平衡时,在介质中传输的光束即形成空间光孤子,又称自导光束.由于在光信息处理、全光开关、光波导和光互联器件等方面的应用前景,空间光孤子得到了众多学者的广泛关注,特别是近几年对非局域材料中空间孤子的研究[1-14],目前常见的非局域材料有向列相液晶[2-4]、热致非线性铅玻璃材料[5-7]和非局域 kerr介质[8-14]等.文献[3]采用Gauss形式的试探解,对向列相液晶中非局域空间孤子的传输进行了理论研究,得到Gauss孤子和临界功率附近呼吸子的解析解;文献[4]不仅从理论上得到了液晶孤子传输的解析解,而且从实验上观察了空间光孤子在向列相液晶中的传输,找到不同束宽下空间光孤子的临界功率;李少华等人研究了不同形状铅玻璃对各阶厄密高斯光束稳定传输的影响[5];Dong等人用数值模拟方法研究了铅玻璃中(1+1)维多级孤子的稳定性,得出基孤子和偶极孤子均可以在存在的区域内稳定传输,三极以上孤子的不稳定区域随样品宽度的增加而增大[6];Bai等人以普遍意义的ψ(x,z)=u(x)exp(iλz)形式波函数作为(1+1)维Kerr介质中 H-G光束簇的试探解,利用变分法研究了其传输的物理特征,并用数值法观察了不同非局域程度下光束传输的稳定性,得出传播常数λ是介质非局域程度的量度[8];而后,杨振军等人利用变分法对Kerr介质中的一类反向两极孤子模型进行研究,得到m不同时描述该类孤子的参数耦合方程,并通过数值模拟得到光束能量不同时两极孤子的传输规律和克尔介质中m=0时高斯孤子的参数耦合方程,但并没有给出m=1时偶极孤子的具体参数耦合方程[9].
本研究对无限非局域铅玻璃介质中(1+1)维的偶极稳态孤子解进行求解,假设偶极孤子的试探解为具有普遍意义的带有传播常数项exp(iλZ)形式的波函数,利用变分法求解出该形式下描述偶极孤子稳态解的一般参数耦合方程组,解释传播常数在此系统下的物理意义,并通过数值模拟验证了变分计算结果和在该参数方程组制约下形成的偶极孤子的稳定性.偶极孤子是高阶孤子的最简单形式,本研究对偶极孤子稳态解参数耦合方程组的求解是对非局域铅玻璃介质中偶极孤子解析解的普遍描述,为寻求更高阶孤子具有普遍意义的形式解埋下伏笔,并为研究热非线性系统中高阶孤子的相互作用及其偏转特性奠定了基础.
1 理论模型及其偶极孤子解
在不考虑损耗的情况下,(1+1)维傍轴光束在非局域热非线性铅玻璃介质中的传输可以用非局域非线性薛定谔方程和泊松方程来描述[5-7]
耦合方程组式(1)和式(2)是归一化后的结果,但由于其变分问题比较难解,为此先假设一试探解.偶极孤子是高阶孤子的最简单形式解,这里选取具有普遍意义的(1+1)维偶极波函数ψ(X,Z)作为式(1)的偶极孤子试探解

设正方形截面铅玻璃介质的宽度为2d,偶极光束由介质对称中心入射并沿Z轴方向传播,光束热源入射对介质进行加热,热扩散效应会引起介质折射率N的变化,易知有边界条件


式(17)表明传播常数λ是表示偶极孤子功率大小的参量,它与介质半宽度有关,随着宽度的增大而增大.
因为d≫W,图1是在介质的半宽度d=10时,传播常数λ与功率P的对应关系图(P取正值).由图1可知,每个入射功率P都有相应的传播常数λ与之对应,即传播常数λ是代表孤子功率大小的量,
试探波函数复相位中的传播常数λ不同则表示形成的孤子具有不同的能量.

图1 孤子功率P随传播常数λ变化的关系图Figure 1 Power P versus the propagation constantλfor dipole solitons
根据式(13)可知,孤子振幅的平方(B2)与束宽的六次方(W6)具有反比关系,二者乘积为一常数.图2为由式(13)决定的孤子振幅B随束宽W变化的曲线图,由图2可以看出,偶极孤子的振幅B随束宽W的增大而不断减小,即铅玻璃介质中的入射光束束宽越宽,则形成偶极孤子的振幅越小,光强越弱.

图2 振幅B随束宽W变化的曲线图Figure 2 Amplitude B versus the beam width W for dipole solitons
综上所述,在正方形截面的热非线性铅玻璃介质中,当介质半宽度d远大于偶极入射光束束宽W时,对于试探波函数参数中给定的一组(d,λ)值,根据参数耦合方程组式(13)、式(15)和式(16)可以很容易得到关于稳态偶极孤子试探解的参数(W,B和P)的值,写出可以形成偶极孤子的具体波函数解析解,从而确定该偶极孤子所具有的能量和光强度.传播常数λ是代表孤子功率大小的量,只要λ,W和B满足上述偶极孤子参数耦合方程,理论上都可以得到铅玻璃介质中具有不同功率的稳定偶极孤子解析解,如果假设成立则表示此参数耦合方程组式(13)、式(15)和式(16)具有一般意义.同时,在正方形截面的热非线性铅玻璃介质中,偶极孤子振幅平方(B2)与入射光束束宽六次方(W6)的乘积为一定值,孤子振幅B随束宽W的增大不断减小,即入射铅玻璃的光束束宽越宽,形成偶极孤子的振幅越小,光强越弱;传播常数λ是表示偶极孤子功率大小的参量,同时还与介质半宽度有关,它随宽度的增大而增大,即试探波函数复相位中的传播常数λ越大表示形成的孤子具有的能量越强.
2 数值模拟
为了验证通过变分法得到的计算结果,即不同λ能否都形成很好的偶极孤子稳定传输,参照上面得出的参数耦合方程组式(13)、式(15)和式(16),采用对称分步傅里叶法对式(3)和式(4)进行数值模拟.假设初始光束采取如下形式:

式(18)中,λ,W和B满足参数耦合方程组式(13)、式(15)和式(16),这里取介质半宽度d=10,此时偶极光束在该铅玻璃介质中的传播规律模拟图如图3所示.
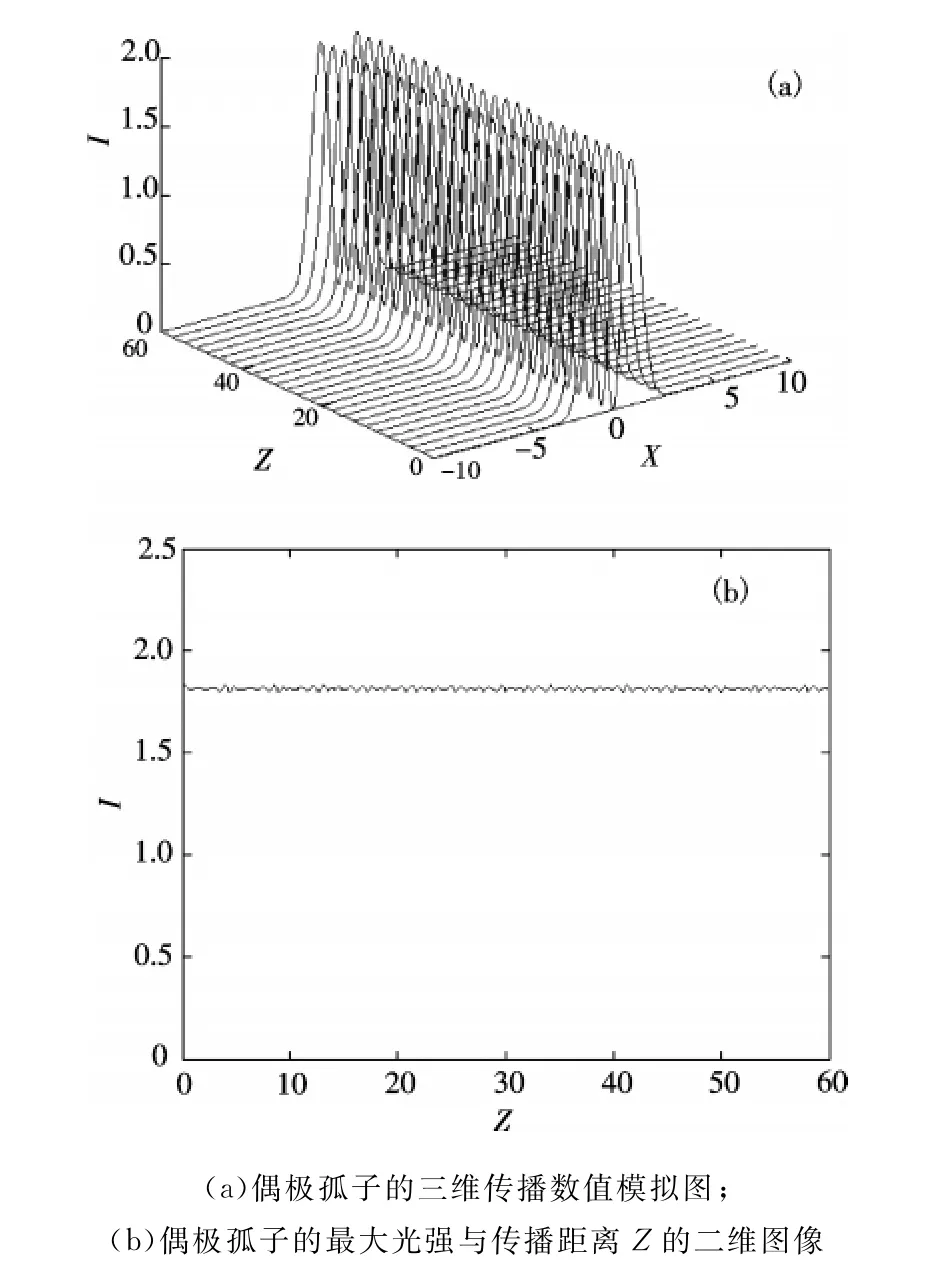
图3 d=10,λ≈17.735 4,W=1,B≈2.202 0,P≈4.297 1时,铅玻璃介质中的传播规律模拟图Figure 3 Dynamic propagation of dipole solitons when d=10,λ≈17.735 4,W=1,B=2.202 0,P≈4.297 1
图3(a)为λ≈17.735 4,W=1,B≈2.202 0,P≈4.297 1时,数值模拟偶极试探解在非局域铅玻璃中的三维传播图,图中X轴表示介质的横向宽度从-10~10个归一化距离,Z轴表示偶极孤子的传播方向和60个瑞利距离,纵轴表示孤子的光强I=
|U|2.取W=1是为了验证将式(13)、式(15)和式(16)制约的参数带入波函数试探解是否能在此系统下形成孤子.由图3(a)可以看出,根据由参数耦合方程得出的各参数模拟出的结果理想,偶极孤子在传播了60个瑞利归一化距离或是更远都可以保持稳定.图3(b)是在同样的参数条件下,较细致地观察图3(a)所对应的偶极孤子最大光强与传播距离Z关系的二维图像,可以看到图3(a)中孤子的光强确实保持不变,几乎为一条水平直线,证明了该孤子的传播具有良好的稳定性.
为了验证参数方程式(13)、式(15)和式(16)的普适性,分别取束宽W大于1和小于1的情况,即λ=25,W≈0.898 2,B≈3.038 7,P≈5.930 0和λ=10,W≈1.193 7,B≈1.294 6,P≈2.526 3两种情况,验证两种条件下的光束是否均可以形成很好的偶极孤子并传输稳定,图4和图5分别为2种情况下典型孤子的传播图像.
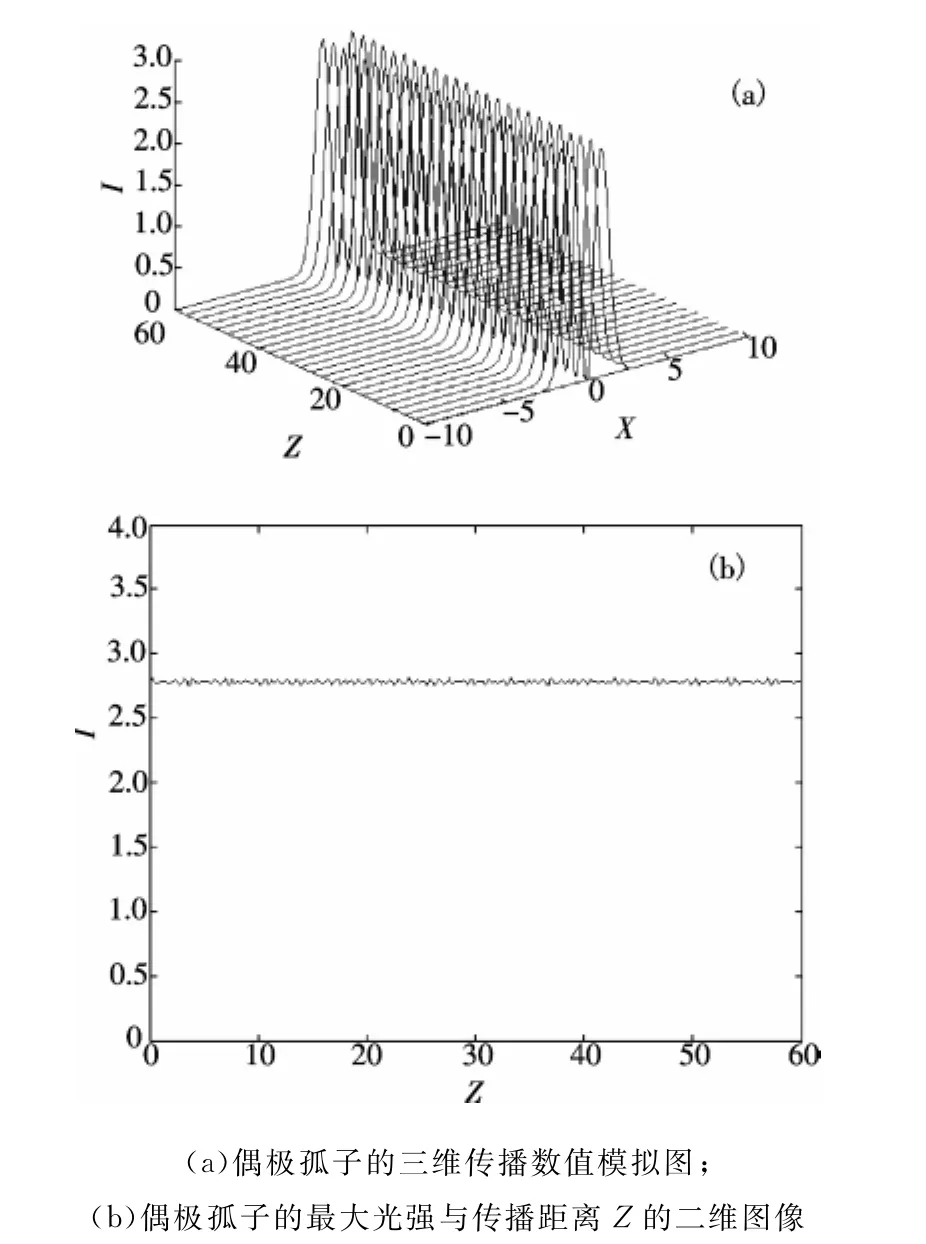
图4 d=10,λ=25,W≈0.898 2,B≈3.038 7,P≈5.930 0时,典型孤子的传播图像Figure 4 Dynamic propagation of dipole solitons when d=10,λ=25,W≈0.898 2,B≈3.038 7,P≈5.930 0
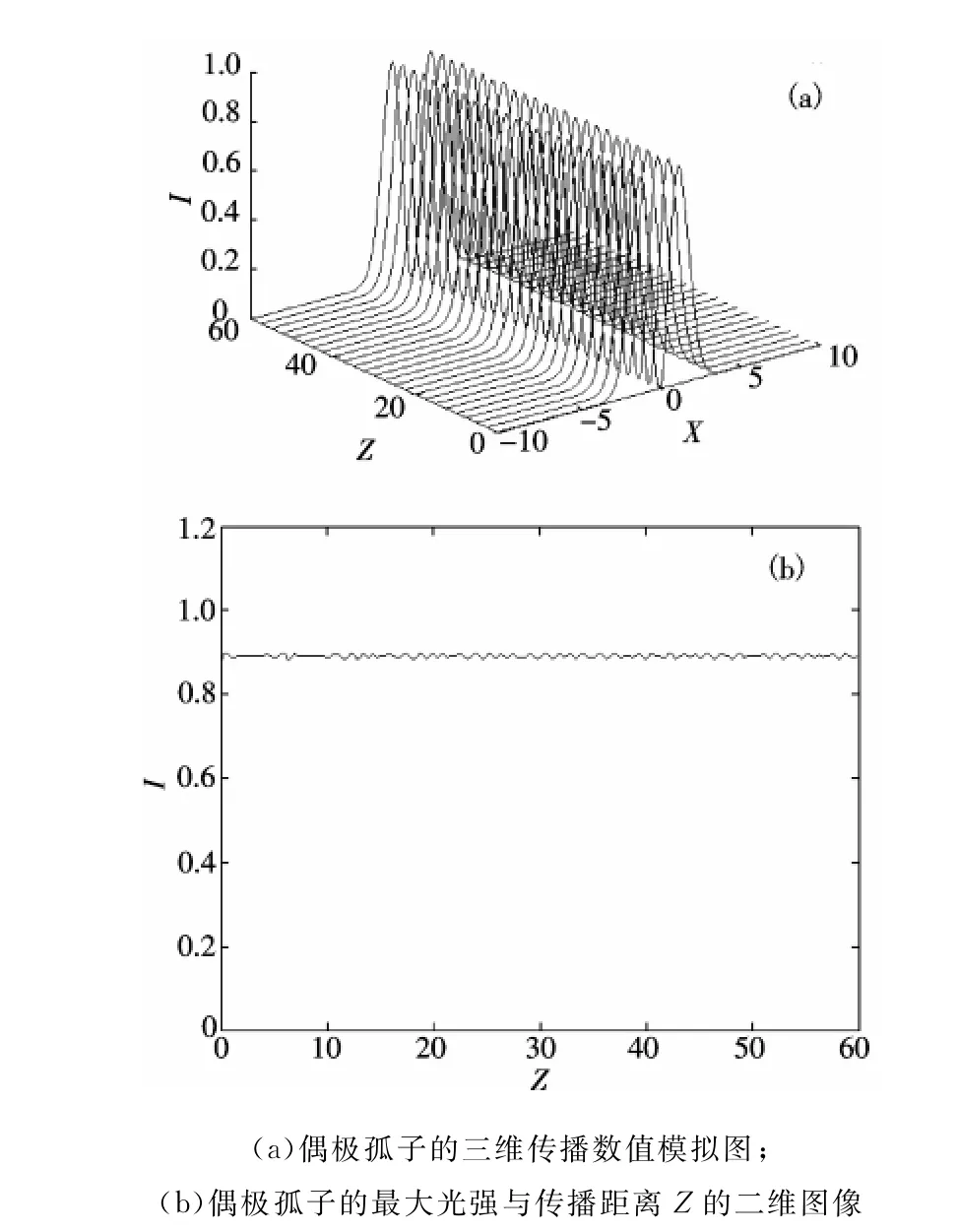
图5 d=10,λ=10,W≈1.193 7,B≈1.294 6,P≈2.526 3时,典型孤子的传播图像Figure 5 Dynamic propagation of dipole solitons when d=10,λ=10,W≈1.193 7,B≈1.294 6,P≈2.526 3
由图4(a)和图5(a)可以看出两组参数情况下,根据参数耦合方程得出的由各参数确定的试探解都可以模拟出很好的偶极孤子,且孤子在传播了60个瑞利距离或更远时仍保持稳定.图4(b)和图5(b)是相应条件下,偶极孤子三维传播数值模拟图中偶极孤子最大光强与传播距离Z关系的二维图,图中孤子的光强均基本保持不变,说明铅玻璃介质中形成了偶极孤子,孤子传播的稳定性很好.
从以上3组随机选取的参数所形成的偶极孤子在热非线性铅玻璃介质中传输的数值模拟图可以看出,根据参数耦合方程,对于给定的一组(d,λ)值,都能够找到很好地形成偶极孤子参数B,W和P与之对应,进而得到该系统具体的波函数解,且形成的孤子可以稳定传输60个瑞利距离或更远,说明偶极孤子参数耦合方程的正确性,证明其确实具有一般意义,同时表明前面所假设的带传播常数项exp(iλZ)形式的试探解是热非线性耦合方程很好的近似解,验证了变分法计算结果的正确性.
3 结论
本研究针对非局域热非线性系统中(1+1)维偶极稳态孤子解的探究问题,假设系统的偶极孤子试探解为具有普遍意义的带传播常数项exp(iλZ)形式的波函数,利用变分法得到了描述偶极孤子稳态解的一般参数耦合方程;推导出孤子振幅平方(B2)
与束宽六次方(W6)的乘积为一确定常数,且振幅B
随束宽W的增大不断减小;得到传播常数λ、孤子功率P和介质宽度d的关系式,通过图像得出传播常数λ随孤子功率P的增大而增大,表明传播常数是表示功率大小的参量.通过随机取不同参数(λ,
W,B,P)组合带入试探解对系统薛定谔方程与泊松方程构成的耦合方程进行直接的数值模拟,得到较好的偶极孤子传播图像,验证了由变分计算得到的偶极孤子解参数方程的普适性,为研究热非线性系统中高阶孤子的相互作用及其偏转特性奠定了基础.
[1] 张霞萍,郭旗.强非局域非线性介质中光束传输的厄密高斯解[J].物理学报,2005,54(7):3178-3182.
[2] Hu W,Zhang T,Guo Q,et al.Nonlocality-controlled interaction of spatial solitons in nematic liquid crystals[J].Appl Phys Lett,2006,89(7):71111-71113.
[3] 龙学文,胡巍,张涛,等.向列相液晶中强非局域空间光孤子传输的理论研究[J].物理学报,2007,56(3):1397-13103.
[4] 张涛,胡巍,龙学文,等.向列相液晶中强非局域空间光孤子的实验观察[J].光学学报,2007,27(1):1431-1437.
[5] 李少华,杨振军,陆大全,等.厄密-高斯光束在热非局域介质中传输的数值模拟研究[J].物理学报,2011,60(2):24214-24222.
[6] Dong L W,Ye F W.Stability of multipole-mode solitons in thermal nonlinear media[J].Phys Rev A,2010,81(1):13815-13818.
[7] 江群,寿倩,郑亚建,等.非局域空间光孤子在矩形边界铅玻璃中偏转研究[J].物理学报,2010,59(1):329-335.
[8] Bai D F,Huang C C,He J F,et al.Variational solutions for Hermite-Gaussian solitons in nonlocal nonlinear media[J].Acta Phys Sin,2009,18(7):2853-2857.
[9] 杨振军,李少华,陆大全,等.非局域非线性克尔介质中两极孤子的变分解[J].物理学报,2010,59(7):4707-4714.
[10] Krolikowski W,Bang O,Rasmussen J J,et al.Modulational instability in nonlocal nonlinear Kerr media[J].Phys Rev E,2001,64:16612-16619.
[11] Bang O,Krolikowski W,Wyller J,et al.Collapse arrest and soliton stabilization in nonlocal nonlinear media[J].Phys Rev E,2002,66:46619-46623.
[12] Zhao J Y,Wang Q,Shen M,et al.The propagation of dipole solitons in highly nonlocal medium[J].Chin Phys B,2010,19(5):54211-54215.
[13] Shen M,Wang Q,Shi J,et al.Partially coherent accessible solitons in strongly nonlocal media[J].Phys Rev E,2006,73:56602-56607.
[14] 白东峰,郭旗,胡巍.非局域克尔介质中厄米高斯光束传输的变分研究[J].物理学报,2008,57(9):5684-5689.
Investigation of dipole soliton solutions in nonlocal thermal media
CAOYaping,HUANGChunfu
(College of Physics and Electronic Information Science,Tianjin Normal University,Tianjin 300387,China)
A wave function with the propagation constant term exp(iλZ)is assumed as(1+1)D dipole soliton solution in nonlocal thermal media system,and the coupled parameter equations are obtained to describe a series of stable dipole soliton solutions by using the variational method.It is found that the product of square of amplitudeBand six powers of beam widthWis a fixed value,Bwould decrease with the increase ofW.And the propagation constant equation about the dipole soliton power and the width of the thermal media is obtained.It shows that the propagation constant is the quantitative measure for dipole soliton power,which is concerned with the width of the thermal media.Finally,the results of variational calculations are confirmed by numerical simulation,which implies that the incident beam can form dipole solitons and propagate stably under the parameter equations.
nonlinear optics;dipole soliton solutions;thermal media;variational method;propagation constant
O437
A
1671-1114(2011)04-0033-05
2010-07-05
天津师范大学青年教师科研启动基金资助项目(5RL074)
曹雅平(1986—),女,硕士研究生.
黄春福(1977—),男,博士,讲师,主要从事非线性光学和光学空间孤子方面的研究.
(责任编校 纪翠荣)
