基于李群李对称方法求解一类偏微分方程
2011-01-05张晓莉赵小山
张晓莉,赵小山
(天津职业技术师范大学 理学院,天津 300222)
基于李群李对称方法求解一类偏微分方程
张晓莉,赵小山
(天津职业技术师范大学 理学院,天津 300222)
基于李群李对称方法求解一类偏微分方程,得到方程的对称约化和精确解及幂级数解等.
李对称分析;幂级数;精确解;相似约化
自然科学领域中存在大量的线性与非线性问题,而其中许多问题最终可用偏微分方程来描述,因此如何求解偏微分方程一直是数学家和物理学家研究的重要课题,Bucklund法[1]、齐次平衡法[2]、Painleve展开法[3]、Jacobi椭圆函数展开法[4-5]、F展开法[6-7]、双曲正切函数展开法[8]、变换迭代法[9]都是比较成熟的求解方法.其中对称理论在数学、物理学、化学等领域起着十分重要的作用.文献[10]对齐次平衡法进行改进,提出了一个新的相似约化法,该方法等价于直接约化法[11].本研究利用李群方法[12-13]求解一类偏微分方程,李群方法是研究偏微分方程的有力工具之一,应用李群可得到方程的不变群和约化方程.
考虑一类偏微分方程[14]
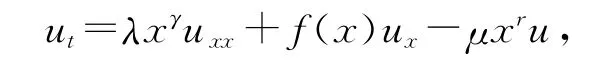
其中,λ>0,μ,γ和r是常数.该偏微分方程具有充分大量的对称群,这类偏微分方程在金融数学及其他领域具有广泛应用.文献[15]得到了方程的李对称积分变换的精确解.本研究利用李对称分析,考虑γ=

本研究所得的一些新的精确解,如幂函数解等是对文献[15]的补充.
1 李群李对称方法的思想

开集M上的向量场,则其第n阶延拓是定义于M(n)的向量场

第二步:利用Maple求出方程(2)的所有生成元(向量场),运用兼容性分别对生成元讨论方程(2)的相似约化和不变量,求出相应的约化方程.
第三步:利用其他方法对约化方程进行求解.这样便利用所求出的生成元得到了变系数偏微分方程的精确解.
2 偏微分方程的李对称分析

3 对称约化和精确解


4 结论
采用李群李对称方法求出了一类偏微分方程的对称,得到了方程的相似约化,并求出了方程的一些新的精确解.
[1] 谷超豪.孤立子理论及其应用[M].杭州:浙江科技出版社,1990.
[2] Wang M L,Zhou Y B,Li Z B.Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J].Phys Lett A,1996,216:67-75.
[3] 楼森岳.推广的Painleve展开及KDV方程的非标准截断解[J].物理学报,1998,9(12):1937-1945.
[4] Dai C Q,Zhang J F.Jacobian elliptic function method for nonlinear differential-difference equations[J].Chaos Soliton Fract,2006,27(4):1042-1047.
[5] Fan E C,Zhang J.Applications of the Jacobi elliptic function method to special-type nonlinear equations[J].Phys Lett A,2002,305(6):383-392.
[6] Abdou M A.The extended F-expansion method and its application for a class of nonlinear evolution equations[J].Chaos Soliton Fract,2007,31(1):95-104.
[7] Fu Z T,Liu S K,Liu S D.Exact Jacobian elliptic function solutions to sinh-Gordon equation[J].Commun Theor Phys,2006,45(1):55-60.
[8] 李志斌,张善卿.非线性波方程准确孤立波解的符号计算[J].数学物理学报,1997,17(1):81-89.
[9] He J H.Some asymptotic methods for strongly nonlinear equations[J].Internat J Modern Phys B,2006,20(10):1141-1199.
[10] 范恩贵.孤立子和可积系统[D].大连:大连理工大学,1998.
[11] 范恩贵.齐次平衡法,Weiss-Tabor-Carnevale法及Clarkson-Kruskal约化法之间的联系[J].物理学报,2000,49(8):1409-1412.
[12] 田畴.李群及其在微分方程中的应用[M].北京:科学出版社,2001.
[13] Olver P J.Applications of Lie Groups to Differential Equations[M].Berlin:Springer-Verlag,1993.
[14] Craddock M,Lennox K A.Lie group symmetries as integral transforms of fundamental solutions[J].Differential Equations,2007,232:652-674.
[15] Craddock M.Fundamental solutions,transition densities and the integration of Lie symmetries[J].Differential Equations,2009,246:2538-2560.
[16] Liu H Z,Li J B.Lie symmetry analysis and exact solutions for the short pulse equation[J].Nonlinear Analysis,2009,71:2126-2133.
[17] Liu H Z,Li J B,Liu L.Lie group classifications and exact solutions for two variable-coefficient equation[J].Applied Mathematics and Computation,2009,215:2927-2935.
Solving a kind of partial differential equations by Lie group Lie symmetry
ZHANG Xiaoli,ZHAO Xiaoshan
(School of Science,Tianjin University of Technology and Education,Tianjin 300222,China)
A kind of nonlinear partial differential equations is solved by the Lie symmetry analysis and group classifications.As a result the symmetry reduction and some new exact solutions have been obtained,including the power series solution and so on.
Lie symmetry analysis;power series method;exact solution;similarityreductions
O175.2
A
1671-1114(2011)04-0020-03
2010-11-09
天津市自然科学基金资助项目(08JCYBJC12100)
张晓莉(1983—),女,硕士研究生.
赵小山(1968—),男,副教授,博士,主要从事非线性动力系统稳定性分析及应用统计方面的研究.
(责任编校 马新光)
