导管架平台的疲劳损伤计算方法研究

施昌威，程承吉，张 丽

（1.中国石油集团海洋工程有限公司工程设计院，北京 100028；2.中国石油青海油田分公司冷湖油田管理处，青海海西817400；3.新疆油田公司克拉玛依物业公司，新疆克拉玛依 834000）

导管架平台的疲劳损伤计算方法研究

施昌威1，程承吉2，张 丽3

（1.中国石油集团海洋工程有限公司工程设计院，北京 100028；2.中国石油青海油田分公司冷湖油田管理处，青海海西817400；3.新疆油田公司克拉玛依物业公司，新疆克拉玛依 834000）

导管架平台在服役期间承受风、浪、流、冰的作用，如何准确评估导管架平台在海上复杂环境条件下的疲劳损伤是海洋工程界面临的一大难题。文章结合Miner线性法则、Paris公式和Manson公式，分析了单一谱载荷作用下导管架的疲劳损伤，探讨了随机载荷作用下海上导管架的总疲劳损伤的计算方法，并给出算例。

导管架；疲劳；裂纹；损伤；分析计算

渤海湾是中国海上油气勘探开发的重要领域，同时也是中国石油集团海洋工程的主战场之一。渤海湾海况恶劣，导管架平台长期承受海水的腐蚀，海浪、海冰、地震、风、特殊机械等载荷的作用，由于裂纹的萌生与扩展，有可能突然发生疲劳断裂，造成生命和财产的严重损失。如：1968年，渤海老二号平台被冰推倒，事故的本质原因是冰激振动产生的疲劳损伤发展到一定程度后，疲劳裂纹的低温脆性扩展而使桩腿失去了承载能力[1]；1980年，“Alexander Keyland”号半潜式平台在北海倾覆沉没，造成123人死亡，事故是由于一根撑杆发生疲劳破坏引起平台整体强度不足造成的[2]。因此，研究估算海上导管架的疲劳寿命具有十分重要的意义。

目前，疲劳分析的传统方法是先分析单一谱载荷作用下的疲劳损伤，再对随机载荷作用下的总损伤采用单一谱载荷损伤线性相加的方法获得。由于不同类型的谱载荷作用在导管架上产生的响应不同，传统线性相加的方法求得的损伤相对于实际情况偏大，从安全角度考虑，传统做法是可取的，但面临尽可能降低成本的经济压力，需要对导管架的疲劳寿命做出更准确的评估。本文在Miner线性准则、Paris公式和Manson公式[3]的基础上进一步推导，探讨随机载荷作用下的疲劳分析公式，供同行参考。

1 Miner线性累积疲劳损伤准则

1945年，Miner提出了线性累积疲劳损伤准则，指材料的总损伤等于每种载荷单独作用于无损伤材料所产生损伤的线性迭加[4]。这种模型的数学表达通式为：

式中D——总疲劳损伤；

N——载荷作用次数；

Nf——给定应力幅 （应变幅）下的疲劳寿命，以总循环次数计；

β——与应力幅 （应变幅）有关的参数，其物理概念是总损伤，当β=1时：

显然，式 （2）即为Miner线性累积损伤模型。若应力幅 （应变幅）水平是变化的，则总损伤为：

式中ni——在应力幅作用下，材料的实际循环作用次数；

Ni——在该应力幅作用下的疲劳寿命。

2 基于Pairs公式的推导

导管架平台在服役过程中受风、浪、流的长期作用，地震是偶然和瞬时载荷，冰是特殊区域载荷（如我国渤海和黄海北部，每年冬季都有海冰出现）。海浪和海冰是结构设计最重要的环境载荷，对结构的疲劳起控制作用。本文针对在海冰和海浪交替出现的环境条件下，对导管架结构的疲劳损伤进行分析。

在不同类型载荷谱的作用下，若采用线性累积疲劳损伤模型，则未考虑载荷之间的相互作用。本节基于线弹性断裂力学中的应力强度因子描述裂纹的扩展特性，即通过Pairs公式来进一步推导[5]：

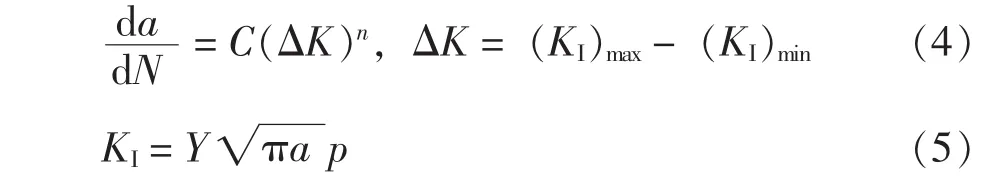
式中a——裂纹的特征尺寸；

C——材料常数；

ΔK——应力强度因子幅值；

（KI）max——最大应力强度因子；

（KI）min——最小应力强度因子；

Y——裂纹几何和结构物几何的作用；

p——描写外场 （机械外应力、或温度激发的外应力等）的作用。

则其疲劳寿命为：

式中a0——裂纹初始尺寸；

ac——裂纹临界尺寸。

式中K——Boltzmann常数；

δ——外场应力。

[2]得：

式中U2、A——材料常数；

T——绝对温度。

将C和ΔK代入式 （6），得：

假设导管架在某服役阶段中承受三种谱载荷的作用 （具体根据工程中实际情况确定），考虑三种载荷产生的累积裂纹等于等效应力作用下产生的裂纹：

3 基于Manson公式的推导

考虑某些导管架在服役中由于工程要求，需要改造或另作他用，载荷会发生变化 （如：前期作为单点系泊装置，后期改造为风机塔架等）。类似公式 （18），后一阶段的等效循环次数N2可用公式（19）表达，即：

式中C1、C2、C3——分别为第二阶段另外三种谱载荷作用下的材料常数；

ΔK1、ΔK2、ΔK3——分别为第二阶段三种谱载荷作用下的应力强度因子；

n1、n2、n3——分别为第二阶段三种谱载荷作用下的实际循环次数；

Na、Nb、Nc——分别为第二阶段三种谱载荷作用下的许用循环次数。

导管架在前后两阶段的疲劳损伤，可采用最简单的Miner线性累积损伤法则，第二阶段的使用寿命T后为：

式中T后——第二阶段的使用寿命；

N前——第一阶段的等效循环次数；

N后——结构改造后第二阶段的等效循环次数；

n——第一阶段的使用年数；

N——总累积循环次数。

传统的Miner线性法则计算较方便，但没有考虑前后两阶段之间的相互作用，一般说应力历史对高应力疲劳寿命影响较小，对低应力影响较大，参考Manson从实验基础上建立的模型[3]，试样在应力S1下循环n1周后，下一级应力下的剩余寿命n2为：

式中N1、N2——一、二级应力下的许用循环次数；

NP——材料的静强度许用循环次数。

Manson考虑了两级载荷的疲劳循环次数，在Manson理论的基础上进一步推导可得，三级载荷下的剩余许用循环次数为：

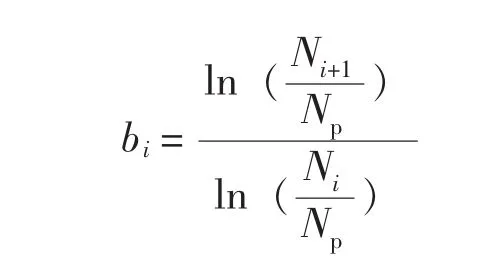
将式 （18）、 （19） 代入式 （21）， 这里 N1即为第一级荷载等效循环次数N前，N2即为第二级荷载等效循环次数N后，相应有n1即n前，n2即n后，于是可得，

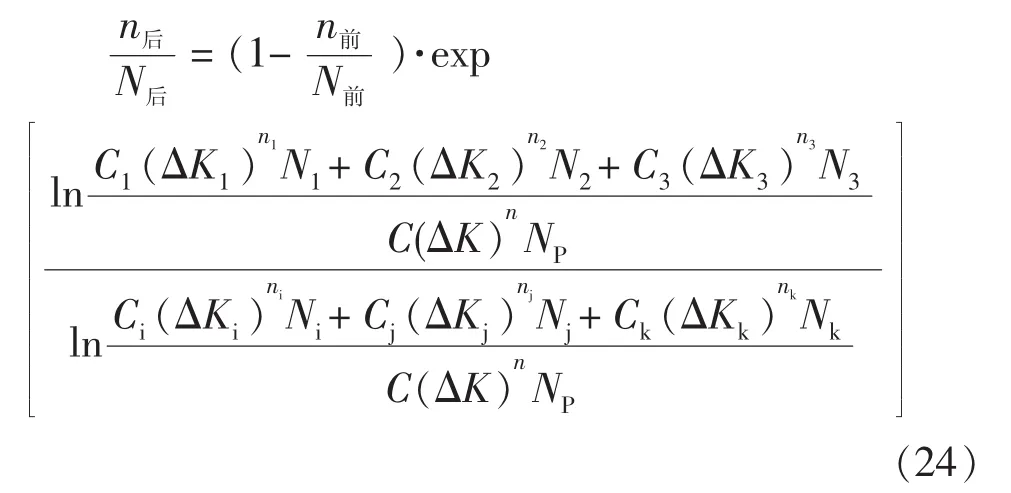
式中n前——导管架在单点系泊阶段的实际循环次数；

n后——导管架在后期改造阶段的剩余许用循环次数。

4 两种算法的计算及对比

以某油田的单点导管架为例进行计算分析。该平台为四桩腿的导管架，导管架在服役过程中经历两个阶段[6]：单点系泊阶段 （1989～2009年），承受海冰、波浪、FPSU系泊载荷的作用；FPSU解脱阶段 （2009年以后），承受海冰、波浪的作用。

4.1 传统Miner线性损伤方法计算结果

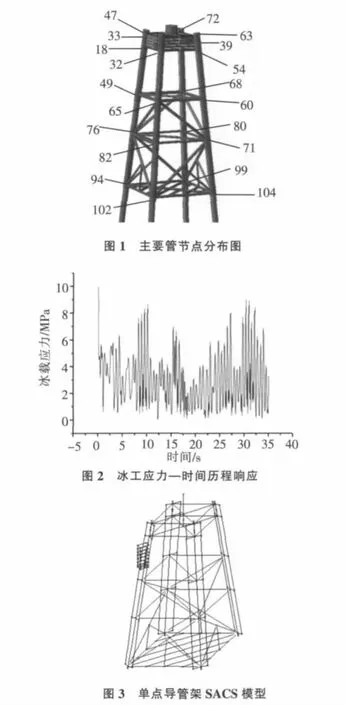
单一载荷的疲劳损伤计算方法已经较成熟，导管架的损伤研究主要关注管节点处，图1为主要管节点分布图。图2为冰激振动计算中提取的冰载应力—时间历程响应，结合API RP 2A[7]的S-N曲线和雨流计数法，可获得冰激载荷[8]和FPSU系泊载荷年损伤。图3为单点导管架SACS模型，图4为单点导管架三维示意，通过SACS软件可以获得波浪载荷的年损伤。这样可以分别获得单一载荷作用下的疲劳损伤和载荷作用次数。

根据公式 （3），即传统Miner线性累积疲劳损伤算法，这三种载荷作用下导管架的总疲劳损伤可以用各自单独作用下的疲劳损伤按式 （25）计算：

式中D——总损伤；

DI、DS、DW——冰激、FPSU系泊、波浪单独作用下导管架的疲劳损伤。

根据公式 （25）得到的导管架的年损伤计算结果列于表1。

取管节点中最小的寿命为导管架的使用寿命，由表1可得，99号管节点的疲劳寿命最短，为64年。

4.2 基于Pairs公式及Manson公式的计算结果

由于作用在导管架上的冰激振动载荷、FPSO载荷以及波浪载荷三者的频率相差较远，各自引起的导管架动力响应具有完全不同的形式，因此，根据传统Miner线性累积疲劳损伤可得，这三种载荷作用下导管架的疲劳损伤可以用各自单独作用下的疲劳损伤按式 （24）计算获得，参考有关文献，式 （24）经化简后得式 （26）， 计算结果列于表1。

根据式 （26）、 （27） 得到的导管架的损伤计算结果列于表1。

表1 导管架主要管节点的年损伤 （安全系数取2）

取管节点中最小的寿命为导管架的使用寿命，由表1可得，99号管节点的疲劳寿命最少，为90年。

5 结论

本文对海上导管架在复杂环境条件下的疲劳损伤进行了较深入的研究，在Paris公式和Manson公式的基础上进一步推导，将多种载荷对导管架疲劳的影响综合在一起，对多载荷谱工况下的疲劳损伤问题进行了探讨。该算法与传统方法相比，传统方法趋于保守，而本算法获得的疲劳寿命更长，从经济上考虑相对节约成本。

该文的创新之处：对各单一工况下，特别在随机冰载和波浪载荷交替作用下，海上导管架的疲劳损伤进行了计算；结合Miner法则和Paris公式，对组合工况作用下导管架的疲劳损伤及裂纹扩展进行了较深入的探索，为同行开展进一步研究打下了较好的基础。

参考文献：

[1]方华灿．渤海采油平台低温冰载作用下设计问题的研究[J].石油矿场机械，1995，24（1）：2-8.

[2]龚顺风．海洋平台结构碰撞损伤及可靠性与疲劳寿命评估研究[D].杭州：浙江大学，2003.

[3]方华灿．海洋石油钢结构的疲劳寿命[M]．东营：石油大学出版社，1990.

[4]Miner M A.Cumulative damage in fatigue[J].Journal of Applied Mechanics，1945，（12）：1-2.

[5]Pairs F A.Critical analysis of crack propagation laws[J].Journal of basic engineering，1963，（8）：2-3.

[6]刘杰鸣．单点系泊导管架疲劳分析[J]．中国海上油气，2003，15（3）：22-24.

[7]API RP 2A-WSD，Recommended Practice for planning,designing and Constructing Fixed Offshore Platforms——Working stress Design（2000）[S].

[8]段梦兰．海冰环境中海洋石油钢结构的破坏分析[J]．石油学报．1999，20（3）：72-76.

Research on Fatigue Damage Calculation Method for Jacket Platform

SHI Chang-wei（Engineering Design Institute of China National Petroleum Offshore Engineering Co.,Ltd.,Beijing 100028,China）,CHENG Cheng-ji,ZHANG Li

A jacket platform works under the wind,wave,ice （in special area） and mechanical loads in offshore conditions,it’s a major challenge to accurately assess the jacket damage in complicated environments.This paper analyzes the fatigue damage under the action of single spectrum load and derives a new formula from the Miner linear rule,Paris formula and Manson formula,and discusses the calculation methods for the total fatigue damage under random loads.And it gives a calculation example.

jacket;fatigue;crack;damage;analytic calculation

TE951

B

1001－2206（2011）增刊－0017－05

施昌威 （1984-），男，湖北仙桃人，助理工程师，2009年毕业于长江大学机械工程学院，硕士，主要从事海洋工程平台结构设计研究工作。

2011-08-10；

2011-08-23