数学软件Mathematica在积分计算中的应用

2011-01-04王绍恒高成政刘雪莲吴梦蝶

重庆三峡学院学报 2011年3期

欧鹏王绍恒高成政刘雪莲吴梦蝶

（重庆三峡学院数学与统计学院，重庆万州，404100）

借助数学软件辅助教学多年以来，[1]收到了较好的效果.积分是高等数学系列课程的重要组成部分，某些题目的积分计算量较大，过程繁琐，甚至无法用学过的数学方法求解.为使学生借助Mathematica软件快速、准确地解决上述问题，笔者结合实验与学习经历，通过借助Mathematica软件计算积分的典型例子，总结了几种常见方法，供读者参考.

1 不定积分

Mathematica软件的命令格式：Integrate[f[x]，x]，运行的结果就是f[x]的原函数F[x]，但不带任意常数.

1.1 初等函数的不定积分

命令Integrate与命令D表示一对互逆运算，即命令D[f [x]，x]表示函数f [x]对x求导.

含参数不定积分：命令Integrate中，若被积函数含有积分变量以外的变量，运行时均独立于积分变量而把此类变量当做常量.

由此可见，正确指定积分变量的重要性.

积分变量可以为任何表达式.

（其中f( x)可以是任意函数表达式）

大多数情况下，积分可以纯粹的根据诸如指数函数、对数函数和三角函数等基本初等函数进行运算.事实上，如果给出一个仅含这种初等函数的积分，那么Integrate的重要能力之一是如果该积分能用初等函数表示，那么Integrate总能成功计算出结果.

1.2 特殊函数的不定积分

有些函数的不定积分不能用初等函数表示，这里Mathematica软件通常能夠用特殊内部函数表示.

其中LogIntegral[x]为系统内部函数.

有时候为了某种特殊需要，需修改命令Integrate的参数，例如下面的积分不能用初等函数来表示.

如果想加入自己定义的积分规则，需要把函数Integrate的保护属性去掉，即：

运行Unprotect[Integrate]得

{Integrate}

定义自己的积分规则：例如定义函数

sin(cos(a+ bx))的积分为 [,]/ JSinCos a x b.运行Integrate[Sin[Cos[a_.+b_.x_]]，x_]：=JSinCos[a，x]/b之后再运行

退出系统后，对Integrate的修改自动还原.

1.3 无法计算的不定积分

如果不定积分既不能用初等函数表示，也无法用特殊函数表示，Mathematica直接以不定积分形式输出.

2 定积分

2.1 初等函数与定积分

对于简单的定积分，只需按照命令格式输入相应的被积函数，积分变量及积分限即可进行计算.

计算定积分时，也可首先通过先求不定积分，然后计算相应积分限处的值的办法，但值得注意的是有些函数的不定积分不能用初等函数表示，但其定积分仍可以计算.

运行Integrate[Cos[Sin[x]]，x]

Integrate[Cos[Sin[x]]，{x，0，2Pi}]

得2 BesselJ[0，1].

与不定积分一样，在计算定积分的时候，积分变量也可以为任何表达式.对于那些积分变量以外的变量均当作常量处理.

2.2 特殊函数与定积分

在计算定积分时，有时求出来的定积分结果里面含有特殊函数，这些函数是Mathematica内部函数，我们可以对求出的结果取近似值得出近似解.如对例9中的定积分.

运行Integrate[Cos[Sin[x]]，{x，0，2Pi}]得2 BesselJ[0，1]再运行N[%]得4.80788也可以直接运行NIntegrate[Cos[Sin[x]]，{x，0，2Pi}]得到同样结果.

计算定积分时，还可对命令Integrate进行设置参数，通过这些参数设置，可以更加灵活地计算定积分.在我们常见的函数中，参数GenerateConditions以及参数Assumpions使用较多.对于参数GenerateConditions的使用，如设置GenerateConditions-＞False，则 Mathematica会把被积函数中的参数当作最普通的值，不考虑其特殊情况.

例11：运行

Integrate[x^n，{x，0，1}，GenerateConditions-＞ False得1/n+1.不加参数GenerateConditions-＞False的计算结果参看例17.

2.3 数值积分的计算

在Mathematica中，当积分算不出准确值时，我们可以通过NIntegrate[f[x]，{x，a，b}]求近似值.而且对于命令 Integrate能够计算的，NIntegrate也能计算；有些函数不能用 Integrate计算的，用函数NIntegrate还能计算.

此类定积分用人工计算比较复杂，但借助函数Integrate计算较容易.

运行

如果希望得到近似数值解，运行：

NIntegrate[x*Exp[x]Sin[x]，{x，0，1}]得0.643678

对于NIntegrate命令的一个重要的作用是能处理被积函数无界的函数，函数NIntegrate在积分区间内自动检查被积函数有无瑕点，因此对无界函数仍可直接用 NIntegrate 命令计算.NIntegrate[f，{x，xmin，xmax}]会从xmin到xmax积分f，在每个点检查其奇异性.

由于x=0是瑕点，直接用函数NIntegrate将给出出错信息.

如果在5.0版本下运行NIntegrate[1/Sqrt[Abs[x]]，{x，-1，1}]将输出

该提示表明x=0为被积函数的瑕点.我们只要加入0作为中间点，就可以计算其数值解了.

运行NIntegrate[1/Sqrt[Abs[x]]，{x，-1，0，1}]得4.

在7.0以上版本下运行

NIntegrate[1/Sqrt[Abs[x]]，{x，-1，1}]

可以直接得出结果4.

除此之外，数值积分不但可以求近似解，而且还可以设置参数WorkingPrecision的值控制输出结果的精度.

运行NIntegrate[Exp[-x^5]，{x，-1，0，1}，WorkingPrecision-＞20]得

2.094968171321203348 4.

该命令等价于

N[Integrate[Exp[-x^5]，{x，-1，0，1}]，20].

NIntegrate利用自适应算法计算积分的近似值，它对积分区间进行分割，直到达到指定的精确度为止.

2.4 广义积分

无穷区间上的广义积分的计算仍然可行.

如果广义积分发散，Mathematica就给出一个提示后原样输出.

运行

Integrate[1/x^(1/2)，{x，1，Infinity}]输出提示：

如果广义积分的敛散性与某个符号的取值有关，Mathematica也能给出在不同情况下的积分结果.

一般地，我们采用分别讨论a与p的取值，去判断积分收敛或者发散，而利用 Mathematica求解上述广义积分：运行Integrate[1/x^p，{x，a，Infinity}]得

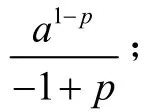
无界函数的广义积分有时要把间断点加入才能计算.

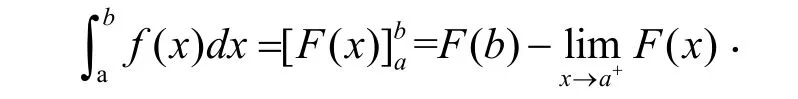
类似地，如果b为瑕点有：

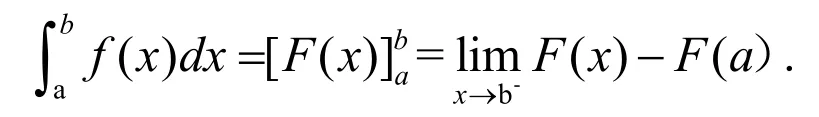
如果c(a＜c＜b)为瑕点时：

2.5 重积分的计算

对于重积分的计算，在Mathematica中，处理方式与定积分相似，只是在处理多个变量积分时，需要给出它们各自的取值范围.

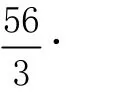
与我们在数学上处理积分时原则一样，Mathematica先对y积分时，积分限可以为x的函数.同时，多重积分限也可以为任何表达式.

运行Integrate[x^2+y^2，{x，a，b}，{y，x，x+1}]得

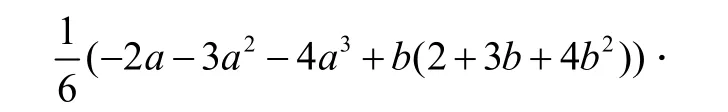
2.6 重积分的可读性计算

运用Integrate求解重积分的确方便快捷.但不足之处是没有体现积分过程.那么运用Mathematica求解积分，到底能不能将其过程展现出来呢？我们的答案是肯定的.只是在求解过程中，要运用到更多的参数选项.其命令格式相对较复杂.

可读性计算程序如下：

Clear[x，y];

f[x_，y_]：=x^2+4y^2+1；Print[“f(x，y)=”，f[x，y]]；

a= -1；b=1；c=-Sqrt[1-x^2]；d=Sqrt[1-x^2]；

If[NumberQ[a]&&NumberQ[b]， g[x_]：=Integrate[f[x，y]，{y，c，d}]；Print[g[x]]；Integrate[g[x]，{x，a，b}]，h[y_]：=Integrate[f[x，y]，{x，a，b}];Print[h[y]]；Integrate[h[y]，{y，c，d}]]

求解过程及结果为：