一种求解最优控制问题的非均匀控制向量参数化方法

雷 阳，李树荣，张 强，张晓东

(中国石油大学信息与控制工程学院，山东青岛 266555)

一种求解最优控制问题的非均匀控制向量参数化方法

雷 阳，李树荣，张 强，张晓东

(中国石油大学信息与控制工程学院，山东青岛 266555)

传统的均匀参数化方法在求解固定终端时刻最优控制问题时，不能精确地逼近最优控制轨迹。针对这一问题，提出一种非均匀控制向量参数化的数值解法。首先将控制时域离散化为不同长度的时间段，各时间段长度作为新的优化参数;然后引入时间尺度因子，将非均匀参数化的最优控制问题转化为标准化时域上的均匀参数化问题;最后建立目标和约束函数的Hamilton函数，通过求解伴随方程计算梯度，采用序列二次规划方法获得数值解。针对两个经典的化工过程最优控制问题进行仿真研究，仿真结果验证了所提出算法的有效性。

最优控制;化工过程;非均匀控制向量参数化;序列二次规划(SQP);固定终端时刻

近年来，为了提高产品质量，节约生产成本，化工过程的最优控制问题(OCP)越来越受到人们重视［1］。由于化工过程大多是复杂的非线性模型，存在各种约束条件，因此要获得一个高质量解通常十分困难。目前，固定终端时刻的OCP数值求解多采用控制向量参数化(CVP)方法［2］。CVP的优点在于它是一种可行路径方法，有效地减少了优化参数和约束条件的个数。但是，CVP中的时间网格通常是均匀划分，并且在优化过程中不会改变，而大多数化工过程的最优控制轨迹都具有切换结构，精确描述切换时间和控制结构显得尤为重要。为了克服均匀 CVP 的缺陷，Binder［3］和 Schlegel等［4］提出了自适应网格划分的CVP方法，在迭代过程中通过对上一步解的小波分析来调整时间节点的划分;Schlegel［5-6］提出了一种自动检测切换结构的CVP方法，将动态优化问题转化为一个多段优化问题，然后重新参数化求解;Hadiyanto［7］通过灵敏度分析，对超过灵敏度阈值的时间段进行细分。这些方法均需要多次求解OCP，过程较为复杂。为有效求解固定终端时刻最优控制问题，笔者提出一种非均匀CVP方法，同时优化控制参数和时间节点。

1 最优控制问题描述

终端时刻固定的最优控制问题可以描述为寻找控制函数u(t)，最小化性能指标如下:

式中，x表示状态向量;u表示控制向量;g为终端时刻状态的非线性约束函数;umax和umin分别为已知的控制上下限;tf为已知的固定终端时刻。

定义Hamilton函数

式中，λ为伴随向量;^x和 ^u分别表示最优状态轨线和最优控制;μ为终端时刻的不等式约束的Lagrange乘子，且满足

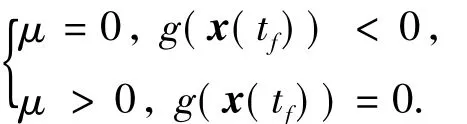
式(6)～(11)所述为一个两点边值问题，直接求解十分困难。目前，OCP的数值求解多采用CVP方法，先将控制时域离散化为等长的时间段，然后在优化时域内对系统模型积分，将OCP中的系统模型约束完全消去，转化为非线性规划(NLP)问题，最后用NLP方法求解，有效地避免了求解两点边值问题。

2 求解策略

2.1 非均匀控制向量参数化

CVP是利用分段函数近似控制作用，进而将OCP转化为NLP问题进行求解的方法［2］。一般可采用分段常数函数、分段线性函数或高阶B-样条函数进行参数化，而且大多数情况下分段常数函数能够很好地完成对控制量的逼近［3-4］，因此本文中采用分段常数近似。

首先，将优化时域［t0，tf］离散化为N个时间段，选取相应的控制时间节点

所谓非均匀控制向量参数化，是指各时间节点之间的间距不相等，除了初始和终端时刻以外，每个时间节点ti均需要优化。若节点间等距，则称为均匀控制向量参数化。

然后，在各时间段内用分段常数函数逼近连续控制量，即

经过参数化处理控制变量以后，形如式(1)～(5)的最优控制问题即可转化为含有N-1个时间节点参数和N个控制参数的NLP问题。

非均匀CVP方法能够同时优化时间节点和控制参数，因此可以很好地逼近复杂的最优控制策略。但是，优化时间节点参数时，需要保证时间节点的先后次序不变，这增加了大量约束条件，而且性能指标J对各个时间节点ti的梯度难以求得。即使可以通过有限差分求得近似梯度，相邻迭代时间节点的不一致也会导致控制参数的更新没有意义。本文中通过引入标准化时间变量，将非均匀参数化的最优控制问题转化为均匀参数化问题求解。

定义每个时间段长度

其中，vi≥0(i=1，2，…，N)。 通过优化各时间段长度vi，可以间接确定出各个时间节点。

引入一个标准化的时间变量τ，在时间段［ti，ti+1］上定义 dτ，使其满足

式中，α为时间尺度因子。这样原控制时域［0，tf］就转化为标准化时域 [0 ，]。对式(15)两边同时

问题(20)的各标准化时间节点τi间距相等，可以采用均匀参数的方法求解。

2.2 梯度计算

对约束OCP(20)，将v(τ)也看作控制变量，定义

首先不考虑末端状态不等式约束对系统的影响，求解目标函数对控制作用的梯度。定义问题(20)中目标函数的Hamilton函数

3 优化算法

针对均匀参数化的OCP(20)，用离散的控制量在优化时域内对状态方程积分，将优化问题中的动态系统模型约束完全消去，得到如下NLP问题:

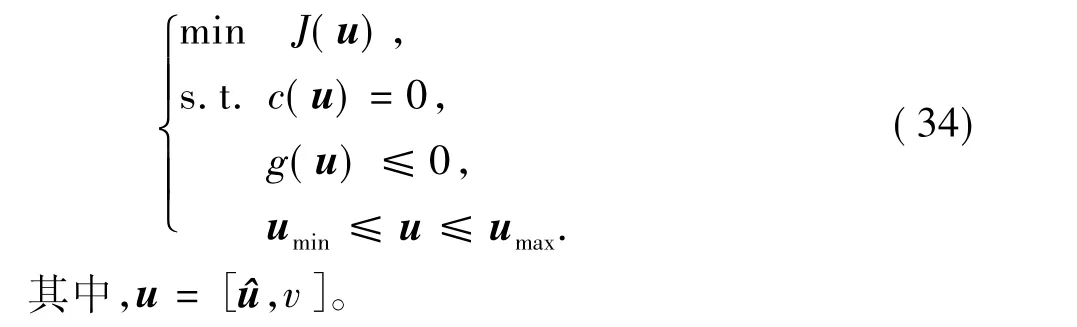
SQP是求解上述约束优化问题的最优方法之一，在非线性规划中已经得到了广泛的应用［8-9］。SQP方法将非线性规划问题转化为迭代求解一系列的二次规划(QP)子问题，其第k步迭代相应的QP问题为

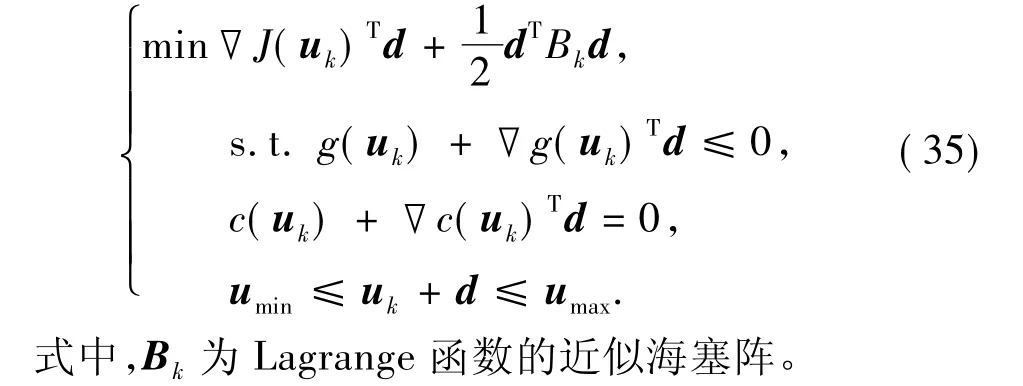
求解QP子问题，得到第k步的搜索方向dk，则第k+1步控制为

搜索步长αk通过一维线搜索获得。具体迭代过程如下:

(1)初始化状态x(0)，控制u(0)，迭代精度ε＞0。初始迭代k=1。

(2)正向求解状态方程获得状态变量值，反向求解伴随方程获得伴随变量值。

(3)利用步骤(2)获得的状态变量和伴随变量值，计算目标函数和终端约束函数的值及各自对决策变量的梯度。

(4)求解第k步QP子问题(34)，生成新的迭代步uk+1。若‖J(uk+1)-J(uk)‖ ＜ε，则获得最优解，迭代结束;否则，令k=k+1，返回步骤(2)继续求解。

4 仿真实例

4.1 化学反应器最优控制问题

Reddy和Husain［10］研究了一类固定终端时刻的化学反应器OCP，可以描述为

分别采用本文中提出的算法与均匀参数化方法求解此问题。对于本文中提出的非均匀参数化方法，时间尺度因子选为α=0.02，时间域经标准化后变为τ∈［0，50］，时间段数N=10。状态变量采用四阶龙格库塔方法计算，仿真步长为0.05。初始控制u(0)=0.25，时间段初始长度v(0)=0.5。采用SQP方法进行数值求解，迭代32步达到最优值J=0.72390。采用均匀参数化方法求解，迭代23步达到最优值J=0.72298，其结果比较见图1。通过结果可以看出，最优控制轨迹在t=0.5796时发生切换，所提出的算法可以精确地指示切换时间，而均匀参数化方法由于时间网格固定，不能很好地描述控制结构。

图1 化学反应器最优控制轨迹Fig.1 Optimal control trajectory for chemical reactor

4.2 酒精发酵最优控制问题

Bojkov［11］研究了一种酒精发酵补料分批反应器模型的固定终端时刻OCP。优化策略是通过控制进料速率和反应时间，使酒精的产量达到最大，具体描述为

式中，x1为生物浓度，g/L;x2为基质浓度，g/L;x3为酒精浓度，g/L;x4为溶液体积，L;C和D分别为比生长率和比生产率，h－1。 初始状态值为 x(0)=［1 150 0 10］T，进料速率的上下限约束为0≤u≤12(L/h)，反应终止时，溶液体积需满足0≤x4(tf)≤200。

首先采用提出的非均匀控制向量参数化方法求解该问题。选取时间尺度因子α=0.02，时间域经标准化后变为τ∈［0，50］，时间段数N=10。状态变量采用四阶龙格库塔方程计算，仿真步长为0.05。初始控制u(0)=3 L/h，时间段长度v(0)=6 h。采用SQP方法进行数值求解，经过98步迭代，获得最优性能指标J=20840。此结果优于文献［11］中的结果(J=20838)和文献［12］中的结果(J=20 747)。然后采用均匀参数化方法求解，经49步迭代，获得最优性能指标J=20663，比较结果见图2。从图2可以看出，最优控制轨迹存在切换结构，虽然最后一个时间段长度较短，但对于性能指标的影响很大。这也说明非均匀参数化方法可以很好地逼近复杂的控制策略。

图2 酒精发酵最优控制轨迹Fig.2 Optimal control trajectory for alcoholic fermentation

5 结束语

针对固定终端时刻OCP，提出一种非均匀CVP方法。将各时间段长度与控制参数同时作为优化变量，可以用较少的时间段数精确地描述控制结构，获得高质量的解;通过时间标准化将原问题转化为均匀参数化问题，利用伴随方法推导出目标函数和约束函数的梯度表达式，采用SQP方法求解，具有较快的收敛速度。两个化工过程最优控制问题的仿真试验证明，非均匀CVP方法在求解固定终端时刻OCP上具有令人满意的数值精度，是求解OCP的一种有效方法。

［1］ENGELL S.Feedback control for optimal process operation ［J］.Journal of Process Control，2007，17(3):203-219.

［2］INGE Spangelo.Trajectory optimization for vehicles using control vector parameterization and nonlinear programming［D］.Trondheim，Norway:Department of Engineering Cybernetics， The Norwegian Institute of Technology，1994.

［3］BINDER T，CRUSE A，CRUZ Villar C A，et al.Dynamic optimization using a wavelet based adaptive control vector parameterization strategy ［J］.Computers ＆Chemical Engineering，2000，24(2/7):1201-1207.

［4］SCHLEGEL M，STOCKMANN K，BINDER T，et al.Dynamic optimization using adaptive control vector parameterization［J］.Computers＆ Chemical Engineering，2005，29:1731-1751.

［5］SCHLEGEL M，MARQUARDT W.Detection and exploitation of the control switching structure in the solution of dynamic optimization problem ［J］.Journal of Process Control，2006，16(3):275-290.

［6］SCHLEGEL M，MARQUARDT W.Adaptive switching structure detection for the solution of dynamic optimization problems［J］.Industrial＆ Engineering Chemistry Research，2006，45(24):8083-8094.

［7］HADIYANTO H，ESVELD D C，BOOM R M，et al.Control vector parameterization with sensitivity based refinement applied to baking optimization［J］.Food and Bioproducts Processing，2008，86(2):130-141.

［8］GOH C J，TEO L K.Control parameterization:a unified approach to optimal control problems with general constraints［J］.Automatica，1988，24(1):3-18.

［9］COSTA C B B，da COSTA A C，MACIEL Filho R.Mathematical modeling and optimal control strategy development for an adipic acid crystallization process［J］.Chemical Engineering and Processing，2005，44(7):737-753.

［10］REDDY K V，HUSAIN A.Computation of optimal control policy with singular subarc［J］.The Canadian Journal of Chemical Engineering，1981，59(4):557-559.

［11］BOJKOV B，LUUS R.Optimal control of nonlinear systems with unspecified final times［J］.Chemical Engineering Science，1996，51(6):905-919.

［12］ARPORNWICHANOP A，SHOMCHOAM N.Studies on optimal control approach in a fed-batch fermentation［J］.Korean Journal of Chemical Engineering，2007，24(1):11-15.

A non-uniform control vector parameterization approach for optimal control problems

LEI Yang，LI Shu-rong，ZHANG Qiang，ZHANG Xiao-dong

(College of Information and Control Engineering in China University of Petroleum，Qingdao 266555，China)

The traditional uniform control vector parameterization method can not obtain accurate optimal control policy when solving optimal control problems with fixed final time.For this reason，a non-uniform control vector parameterization approach was proposed.Firstly，the given time interval was divided into several time stages of varying lengths which were defined as new optimization parameters.Secondly，the original optimal control problem was transformed into a uniform parameterization problem by introducing a time-scaling factor.Finally，the adjoint equations were solved to obtain the gradients by constructing the Hamilton functions of objective and constraint functions.The numerical solution was obtained by sequential quadratic programming method.Simulation results on two optimal control problems of chemical process show the effectiveness of the proposed method.

optimal control;chemical process;non-uniform control vector parameterization;sequential quadratic programming(SQP);fixed final time

TP 273

A >

10.3969/j.issn.1673-5005.2011.05.034

1673-5005(2011)05-0180-05

2011－02－10

国家自然科学基金项目(60974039);国家科技重大专项课题(2008ZX05011)

雷阳(1984－)，男(汉族)，山东阳谷人，博士研究生，研究方向为油田及化工过程最优控制。

(编辑 修荣荣)