黏弹性流体环空内脉动层流流动的理论解析

黄善波，李兆敏

(1.中国石油大学储运与建筑工程学院，山东青岛 266555;2.中国石油大学石油工程学院，山东青岛 266555)

黏弹性流体环空内脉动层流流动的理论解析

黄善波1，李兆敏2

(1.中国石油大学储运与建筑工程学院，山东青岛 266555;2.中国石油大学石油工程学院，山东青岛 266555)

结合运动方程和本构方程，建立同心环空内上随体Maxwell型黏弹性流体在周期性压力梯度作用下脉动层流流动的数学模型，采用固有函数法对模型进行理论求解，得到环空内的速度分布，并讨论各种因素对环空内速度分布的影响。结果表明:受周期性压力梯度作用的影响，环空内的速度随时间呈周期性变化;流体的弹性作用使环空内的速度剖面具有显著区别于牛顿流体的特征。

脉动流;黏弹性流体;Maxwell流体;环空;周期性压力梯度

横截面积均匀一致的同心环空内的流动现象在化学、食品、石油、环境保护等工业领域内有广泛的应用背景。同心环空内牛顿流体与非牛顿流体的定常流动规律已研究得比较充分［1-8］，而在平均值不为零的周期性压力梯度作用下的同心环空内的非定常脉动流中，由于脉动流的物理机制复杂，并具有一定的非常规特性，使这方面的研究具有一定的难度。目前，对圆管内的非定常脉动流已有一定的研究基础［9-16］，而对同心环空内的脉动流，特别是黏弹性流体在同心环空内脉动流的研究报道尚不多见。笔者以上随体Maxwell型黏弹性流体为研究对象，通过理论分析的方法得到其在同心环空内充分发展的层流脉动流的分析解。

1 物理及数学模型

在如图1所示的同心环空内，常物性、不可压缩的黏弹性流体在如下的周期性压力梯度作用下产生了脉动流:

式中，pz为环空内的平均压力梯度，Pa/m;pA为压力梯度脉动的振幅，Pa/m;ω 为脉动的频率，s－1。

忽略黏性耗散效应，并假设流动为已充分发展的层流流动，环空内的速度场可表示为

这样，柱坐标下黏弹性流体的运动方程可简化为

式中，τrz为剪切应力分量。

图1 同心环空的物理模型Fig.1 Physical model of concentric annuli

采用上随体Maxwell模型作为黏弹性流体的本构方程:式中，T为偏应力张量;A为一阶Rinlin-Erickson张量;λ为黏弹性流体的松弛时间，s;η0为流体的零剪切黏度，Pa·s;▽为上随体导数。

根据同心环空轴对称的特点，柱坐标系下本构方程中的τrz可简化为

这就是黏弹性流体环空内脉动流的数学模型。

2 数学模型的求解

式中，Fp(¯t)为非齐次项;Ha是表征黏弹性流体弹性和黏性相对大小的无量纲参数;Rev为脉动雷诺数;A为压力梯度脉动的无量纲振幅;α为环空内外半径之比。

方程(8)为二阶非齐次线性偏微分方程，采用固有函数法［17］进行求解。首先，通过分离变量法得到如下的本征函数:

方程(12)为二阶非齐次线性常微分方程，式(13)是其定解条件之一。为保证解的唯一性还需补充一个定解条件。为此，假设在初始时刻Tm(¯t)为¯t的线性函数，由方程(12)和(13)得到另一个定解条件为

3 计算结果分析

3.1 脉动流速度构成特点

由式(15)可以看出，黏弹性流体环空脉动流的速度分布是由3项构成的，其中空间项Cm(¯r)反映了速度在空间的分布规律，时间项Tmi(¯t)(i=1，2，3)则体现了速度随时间的变化规律。时间项Tmi(¯t)又由两项构成，其中Tmsi(¯t)项中不含有Rev，反映了平均压力梯度对速度分布的的贡献;Tmai(¯t)项中含有Rev，反映了脉动压力梯度对速度的贡献。这样，环空内的速度分布实际上是由两个分速度叠加构成的:一是在平均压力梯度作用下的分速度;二是在脉动压力梯度作用下的脉动分速度。

3.2 几种极限情形

通过对若干极限情形的分析，可以间接地验证上述推导过程的准确性。

3.3 速度分布规律

其他条件相同时(Rev=5.0、A=0.4和α=0.2)不同黏弹性流体在一个稳定脉动周期内不同时刻的速度剖面见图2(Tc为压力梯度的脉动周期)。由图2可见，流体的弹性对环空内速度剖面的形状有决定性的影响。由图2(a)可知，当Ha数较小时，流体的弹性效应不明显，此时环空内任一时刻的速度剖面均近似于抛物型，各点的速度变化同步，与稳态充分发展流动和牛顿流体脉动流时的速度剖面相似。但是，随着Ha数增加，流体弹性增强，速度剖面的抛物线形状逐渐发生变化，环空内各位置处的速度变化不再同步，某些时刻内壁面附近流体和外壁面附近流体的流动方向相反，如图2(b)所示。随着流体弹性的进一步增强，速度剖面呈现出波浪形，而且流体弹性越强，波数越多(图2(c)、(d))。显然，流体的弹性是产生这种变化的根本原因。

脉动Rev数对速度剖面的影响见图3(Ha=1.0，A=0.4，α =0.2)。

图2 不同黏弹性流体的速度剖面Fig.2 Velocity profile in annuli for different viscoelastic fluids

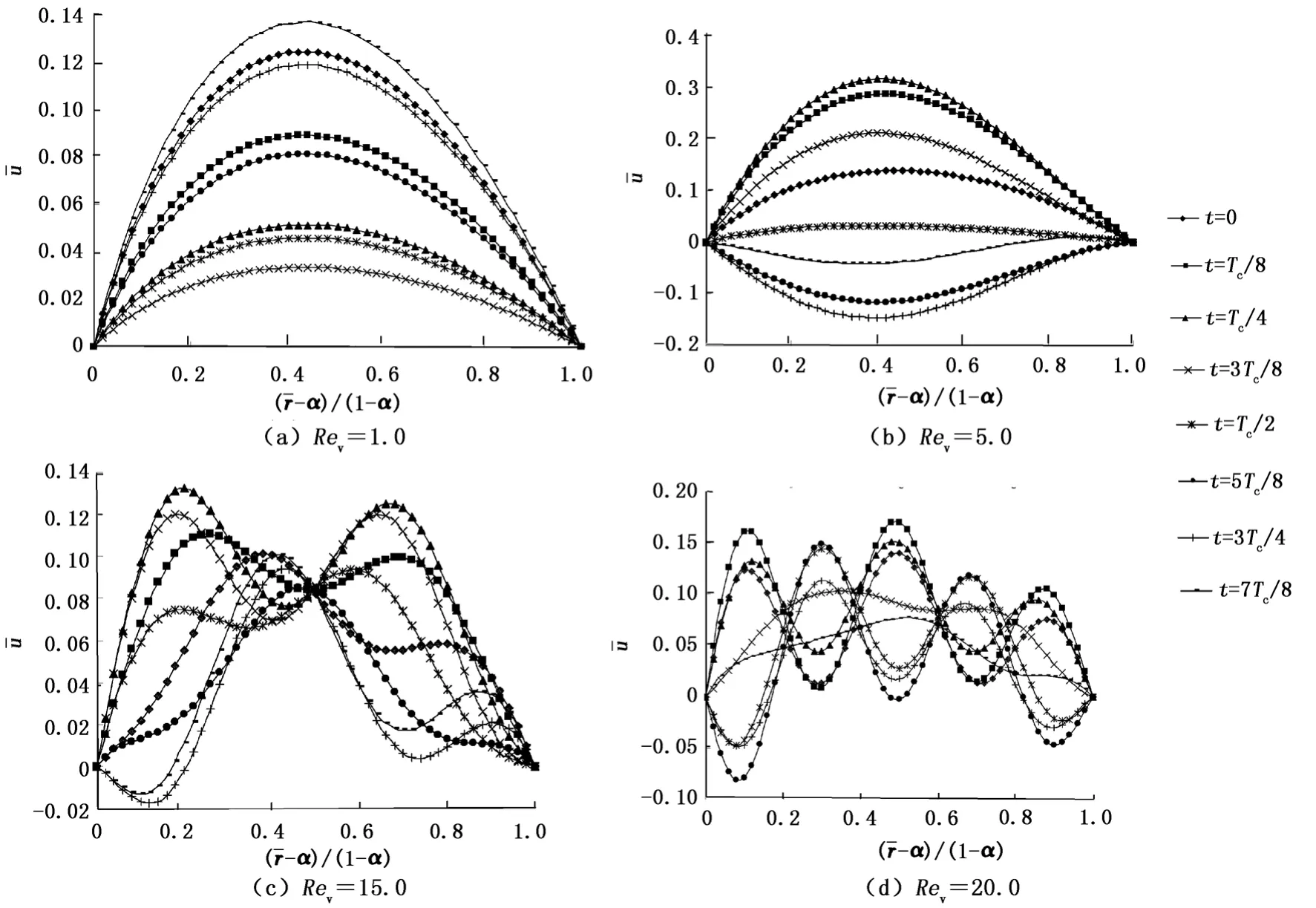
图3 不同Rev数下环空内的速度剖面Fig.3 Velocity profile in annuli for different Revnumber

在Rev数较小、脉动较弱时，环空内各时刻的速度分布均近似于牛顿流体的抛物线型分布。随Rev数不断增加，速度剖面逐渐偏离抛物线型，各点的速度变化也不再同步，并随Rev数增加而出现波浪形分布，并且速度剖面波浪形的波数随脉动的增强而逐渐增多。

压力脉动幅度对速度剖面的影响见图4。图4表明，脉动振幅基本上不改变环空内瞬时速度剖面的形状，但会影响到环空内各点速度变化的幅度。振幅越大，环空内各点速度变化的幅度就越大。

图4 不同脉动振幅下环空内的速度剖面Fig.4 Velocity profile in annuli at different pulse amplitude

4 结论

(1)黏弹性流体环空内的脉动流是由平均压力梯度作用下的分速度和脉动压力梯度作用下的脉动分速度构成的，是流体弹性和压力梯度脉动共同作用的结果。

(2)表征流体弹性的Ha数和表征脉动的Rev数对环空内速度剖面的影响规律相似。随着Ha数和Rev数增加，环空内的速度剖面不再是抛物线型分布，各位置处的速度变化也不再同步，速度剖面呈现出波浪形，而且流体的弹性越强或压力梯度的脉动频率越高，波数就越多。脉动振幅的变化基本不改变速度剖面的形状，但影响速度随时间的变化幅度。

［1］李兆敏，王渊，张琪.宾汉流体在环空中流动时的速度分布规律［J］.石油学报，2002，23(2):87-91.

LI Zhao-min，WANG Yuan，ZHANG Qi.The law of velocity distribution of Bingham fluid's flowing in the encircle pipe［J］.Acta Petrolei Sinica，2002，23(2):87-91.

［2］ESCUDIER M P，OLIVEIRA P J，PINHO F T.Fully developed laminar flow of purely viscous non-Newtonian liquids through annuli，including effects of eccentricity and inner-cylinder rotation［J］.Int Journal of Heat and Fluid Flow，2002，23:52-73.

［3］SHULMAN Z P.Calculation of a laminar axial flow of a nonlinear viscoplastic medium in an annular channel［J］.J Eng Phys，1973(19):1283-1289.

［4］HANKS R W，LARSEN K M.The flow of power-law non-Newtonian fluids in concentric annuli［J］.Ind Eng Chem Fundam，1979，18(1):33-35.

［5］FORDHAM E J，BITTLESTON S H，TEHRANI MA.Viscoplastic flow in centered annuli pipes and slots［J］.Ind Eng Chem Res，1991，30(3):517-524.

［6］PINHO F T，OLIVEIRA P J.Axial annular flow of a nonlinear viscoelastic fluid-an analytical solution［J］.J Non-Newtonian Fluid Mech，2000(93):325-337.

［7］LIU Xi-sheng，ZHAI Ying-hu.An analysis of properties of laminiar flow of power-law fluid in annular space［R］.SPE 14870，1986.

［8］袁谋，李兆敏，王渊.流体的黏弹性对周期性圆管层流流动规律的影响［J］.石油大学学报:自然科学版，2000，24(5):32-38.

YUAN Mou，LI Zhao-min，WANG Yuan.Effect of fluid viscoelasticity on the law of pulsating laminar flowing in pipeline［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，2000，24(5):32-38.

［9］UCHIDA S.The pulsating viscous flow superposed on the steady laminar motion of a incompressible fluid in a circular pipe［J］.Math Phys，1956，7:403-422.

［10］EDWARDS M F，NELLIST D A，WILKINSON W L.Pulsating flow of Non-Newtonian fluids in pipes［J］.Chemical Engineering Science，1972，27:545-553.

［11］黄善波，李兆敏.Maxwell流体在内壁面沿轴向做往复运动的环空内的流动规律［J］.中国石油大学学报:自然科学版，2009，33(4):112-117，124.

HUANG Shan-bo，LI Zhao-min.Law of Maxwell fluid flowing in annuli with inner wall reciprocating axially［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(4):112-117，124.

［12］PHAN-THIEN N.On pulsating flow of polymetric fluids［J］.Journal of Non-Newtonian Fluid Mechanics，1978，4:167-176.

［13］SHEMER L，WYGNANSKI I，KIT E.Pulsating flow in a pipe［J］.Journal of Fluid Mechanics，1985，153:313-337

［14］RAHAMAN K D，RAMKISSOON H.Unsteady axial viscoelastic pipe flow［J］.Journal of Non-Newtonian Fluid Mech，1995，57:27-38.

［15］HAMMAD K J，VRADIS G C.Pulsatile flows of a Bingham plastic in circular pipes［J］.ASME，Fluids Engineering Division，1996，237:685-690.

［16］黄善波，李兆敏.幂律流体同心环空内层流脉动流的数值分析［J］.中国石油大学学报:自然科学版，2011，35(2):127-130，136.

HUANG Shan-bo，LI Zhao-min.Numerical analysis of laminar pulsating flow for power-law fluid in concentric annulus［J］.Journal of China University of Petroleum(Edition of Natural Science)，2011，35(2):127-130，136.

［17］潘忠诚.数学物理方法教程［M］.天津:南开大学出版社，1993:317-341.

［18］黄善波，李兆敏.黏弹性流体环空内的起动流分析［J］.化工学报，2007，58(2):304-309.

HUANG Shan-bo，LI Zhao-min.Analysis of start-up flow of visco-elastic fluid in annular space［J］.Journal of Chemical Industry and Engineering，2007，58(2):304-309.

［19］张捷迁，张光华.真实流体力学［M］.北京:清华大学出版社，1986.

Theoretical analysis of pulsating laminar flow of viscoelastic fluid in annuli

HUANG Shan-bo1，LI Zhao-min2
(1.College of Pipeline and Civil Engineering in China University of Petroleum，Qingdao 266555，China;2.School of Petroleum Engineering in China University of Petroleum，Qingdao 266555，China)

By combining the momentum equation and the constitutive equation，a mathematical model for the pulsating laminar flow of the upper-convected Maxwell viscoelastic fluid under periodic pressure gradient in concentric annuli was set up.The velocity profile was obtained by using the intrinsic function method and the factors influencing the velocity profile were discussed.The results show that the velocity in annuli changes periodically with time due to the periodic pressure gradient.Fluid elasticity is responsible for the difference of velocity profile for Newtonian fluid and non-Newtonian fluid.

pulsating flow;viscoelastic fluid;Maxwell fluid;annuli;periodic pressure gradient

O 337

A >

10.3969/j.issn.1673-5005.2011.05.017

1673-5005(2011)05-0094-05

2011－02－26

教育部重点科学技术研究项目(109158);中国石油大学博士科研基金项目(Y081524)

黄善波(1970－)，男(汉族)，山东文登人，副教授，博士，主要从事非牛顿流体力学理论与应用研究。

(编辑 沈玉英)