倚岸型潮流脊体系中的深槽冲刷——以江苏如东海岸为例
2010-12-28刘秀娟高抒汪亚平
刘秀娟,高抒,汪亚平
(1.中国地质大学资源学院,湖北 武汉 430074;2.南京大学海岸与海岛开发教育部重点实验室,江苏 南京 210093)
倚岸型潮流脊体系中的深槽冲刷
——以江苏如东海岸为例
刘秀娟1,高抒2,汪亚平2
(1.中国地质大学资源学院,湖北 武汉 430074;2.南京大学海岸与海岛开发教育部重点实验室,江苏 南京 210093)
江苏如东海岸的潮流脊体系位于南黄海辐射状沙脊群南部,由沙脊及脊间深槽组成,为“倚岸型”潮流脊体系。本文采用水平一维模型模拟深槽从初始形态冲刷至均衡态的演变过程,用不同的潮差及初始剖面坡度等参数运行该模型,以了解深槽冲刷深度的主要控制因素及其对深槽均衡态的影响。数值实验结果表明:(1) 给定初始剖面的坡度、潮差等参数,经历一定时间的冲刷之后剖面达到均衡态,其后剖面形态保持稳定,不随时间改变;(2) 若仅给定初始剖面的坡度,则潮差越大,达到均衡态时深槽的冲刷深度越大,而且潮差的变化对冲刷深度有显著影响;(3) 若仅给定潮差,则初始剖面的坡度越大,均衡态时深槽的冲刷深度越小且初始剖面坡度的改变对冲刷深度有显著影响。
倚岸型潮流沙脊;均衡深度;潮差;数值模拟;江苏海岸
潮流脊是海岸或大陆架浅海海底特有的地貌形态,形成于沉积物供应充分和潮流较强的环境。潮流脊在世界范围的陆架区分布广泛,根据其一端是否和岸线相连可分为“倚岸型”潮流沙脊和“离岸型”潮流沙脊。国外对潮流脊的研究开始于20世纪60年代,Off于1963年提出了潮流脊 (Tidal Current Ridges) 的概念,并首次将潮流脊与水动力条件联系起来,认为潮流脊是潮流塑造的[1]。之后,学者们对欧洲北海的潮流沙脊进行了研究,探讨其水文、泥沙输运及沙脊形成与维持机制[2-5]。国内从20世纪60年代开始对黄海辐射潮流沙脊群进行研究,如1979-1985年间的江苏海岸带资源调查[6],1990-1995年国家自然科学基金“八五”重点课题“黄海辐射沙洲形成演变研究”等[7],并形成了一系列观点,如:潮流运动是潮流脊发育的动力[8-11];在潮流脊的演变过程中,潮流始终起着主导作用[12];南黄海沙脊群枢纽地区处于增长、扩张过程,南部区域变化较弱而北部变化强烈并继续维持原有的脊槽相间的形状[13],而刘振夏、夏东兴则认为潮流脊的建造力量是纵轴横向环流[14]。遥感和GIS也被用于辐射沙脊群的稳定性研究[15,16]。对辐射沙脊群脊间水道的悬沙浓度垂线分布及悬沙输移的动力机制也进行了初步分析[17]。
国内对潮流脊的形成、演变机制及稳定性的分析主要限于对沙脊群区域潮流场和泥沙运移的数值模拟,而对沙脊间深槽稳定性的动力机制研究还较为薄弱。利用脊间深槽建港或作为航道,其稳定性是一个首要问题,因此本文拟对江苏如东海岸潮流脊体系中的深槽冲刷达到均衡态的演变过程、冲刷深度及主要控制因素进行定量研究,探讨各控制因素对深槽冲刷深度的影响。
1 倚岸型潮流脊特征
江苏如东海岸的潮流脊体系位于南黄海辐射状沙脊群南部(图1),是一个典型的“倚岸型”潮流脊体系,即潮流沙脊的一端和海岸相连,由一系列近似垂直于或斜交于岸线的沙脊及脊间深槽组成。该沙脊体系中的深槽长度一般不超过3 km,水深不超过5 m。如东段潮滩宽度为5 km左右,潮滩坡度在0.05 % ~ 0.09 %。该海区为正规半日潮区,平均涨潮历时6.26 h,平均落潮历时6.11 h。本区的水动力特征为:潮差较大,最大潮差为8.08 m,最小潮差为1.79 m,平均潮差为4.61 m;潮流为往复流性质,涨潮流主流向为240° ~ 300°,落潮流主流向为70° ~ 100°;海流的近底层流速较大,实测最大值为1.4 m/s,大潮时流速大于0.4 m/s。从悬沙浓度分布看,近岸悬沙浓度极高,最高达1.2 kg/m3,向海方向悬沙浓度逐渐降低。本区底质主要由砂质粉砂和粉砂质砂组成,占研究区面积的70%以上,较粗的粉砂质砂主要集中在深槽部位,而砂质粉砂则主要分布在潮流沙脊顶部①。

图 1 研究区概况Fig.1 Study area
2 研究方法
2.1 模型的建立
2.1.1 潮流流速 本文暂不考虑深槽的宽度和沙脊的存在对深槽冲刷的影响,而以一维模型方法模拟深槽水深的变化。如图2所示,BC为潮间带,CD为高潮面,BF为低潮面,坐标原点O设在平均海平面与海岸交界处,设平行于深槽走向且向外海的方向为X轴正向,垂直向下为Z轴正向,A(x,z)为潮下带深槽中的任意一点,则涨潮期间潮间带纳潮量的变化与垂线平均流速的关系为:

①汪亚平,贾建军,高抒,等.江苏洋口港沉积动力学条件与海底稳定性 [R].2003.
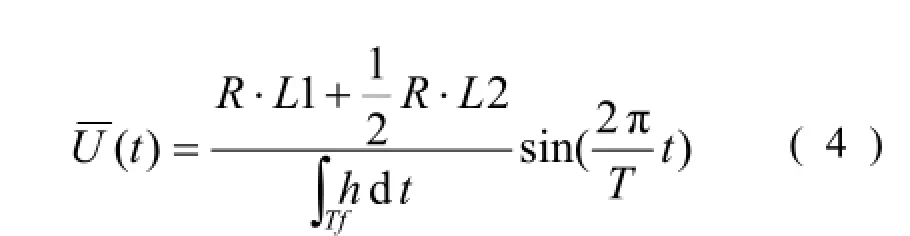

图 2 海岸剖面上以平均海平面与海岸的交点为原点建立的直角坐标系。A(x, z) 为深槽中任意一点,阴影部分为涨潮期间A点以上潮间带纳潮量的变化量Fig.2 Cartesian coordinate system with the origin being located at the intersection of the mean water level on the coast.A(x, z) denotes a point within the channel, and the sheltered area represents tidal prism for the inter-tidal area above the point A
2.1.2 再悬浮引起的泥沙通量 计算潮周期内再悬浮引起的冲刷通量的公式[18]为:

式中:C100为拖曳系数;u100为距离底床1 m处的流速。该沙脊区靠近海岸,水深较浅,因此在水深范围内垂向流速分布满足von Kármán- Prandtl方程:
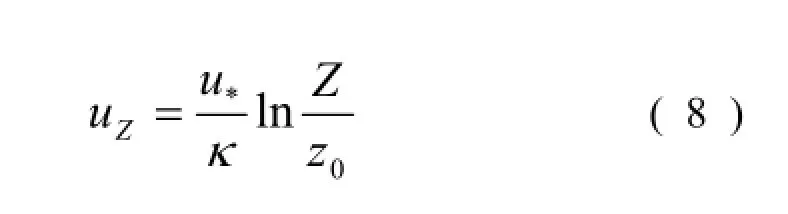
式中:uZ为距床面垂向距离为Z处的流速;u*为摩阻流速;κ为Kármán常数 (=0.4);z0为粗糙长度。从公式 (8) 可得:
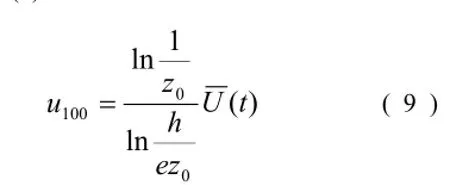
将式 (4) 代入式 (9) 可得海岸形态和水动力之间的关系:
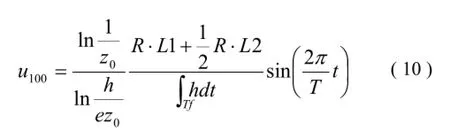
τcr用Shields曲线确定,步骤如下:
(1) 根据实测数据计算出u*或给u*一个经验值;
(2) 根据海水的温度和盐度确定动力粘滞系数υ或直接给出经验值,从下式求出Re*;

(3) 根据Re*在Shields曲线上确定对应的纵坐标θc,然后根据式 (14) 求出τcr。
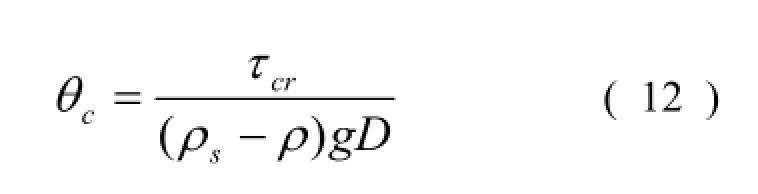
式中:ρs为沉积物密度。
2.1.3 底床变形 深槽底床的变形公式为:

式中:zb表示底床深度;ε表示底床孔隙度。
2.2 模型的运行
2.2.1 冲刷深度计算 如东近岸脊间深槽长度一般不超过3 km,深度一般不超过5 m①。在检验这种方法是否能有效模拟深槽演变至均衡态时的冲刷深度时,深槽长度取为3 km,潮周期为12 h 37',海水密度ρ取1 026 kg/m3,沉积物密度ρs为2 650 kg/m3,涨潮历时为6.26 h①,沉积物粒径D为 3.1×10-5m①,水体运动粘滞系数临界摩阻流速为3.87×10-2m/s[19],粗糙长度z0为 1.98×10-2m[19],C100取经验值3×10-3[20],判定深槽达到冲淤平衡的极小值∆hmin取1.2×10-4m。潮周期内当近底部切应力超过临界切应力时,则计算底床上因再悬浮引起的冲刷通量。
2.2.2 各控制因素对深槽冲刷深度的影响 在探讨潮差和初始剖面的坡度对深槽冲刷深度的影响时,深槽长度仍采用如东近岸潮流深槽通常的长度。为分析潮差对深槽深度的影响,给定初始剖面的坡度,使潮差在2 ~ 6 m范围内变动;为分析初始剖面的坡度对冲刷深度的影响,给定潮差,使初始剖面的坡度在0.05% ~ 0.1%范围内变动。各参数取值见表1。

表 1 模型中各参数取值Tab.1 Values of the parameters for the model
3 模拟结果
3.1 深槽的均衡态
将2.2.1 中如东的相关数据输入模型,计算结果如图3所示,深槽的剖面形态随时间而演变,但变化速度随时间显著减小,并最终趋近于均衡态,即海底的冲淤处于动态平衡之中,剖面形态不随时间改变。在图3中,历时2.5 a与历时3 a的剖面形态是重合的,说明历时2.5 a时剖面形态已稳定,即深槽处于均衡态。深槽均衡态的存在是因为随着深槽的刷深,流速逐渐降低,水流对泥沙颗粒的切应力也随之降低,当小于临界切应力时,水流的切应力不足以起动泥沙颗粒,深槽即处于均衡态。
图3显示,当深槽长度不超过3 km时,均衡态时深槽海图水深不超过5 m,这和如东海岸的“倚岸型”潮流沙脊体系中的深槽深度是吻合的。
3.2 潮差对冲刷深度的影响
当模型的其它输入参数不变而只改变潮差时,则模型运行结果如图4所示,当潮差为2 m时,和初始剖面相比,均衡态时的深槽剖面在左端小范围内有轻微冲刷,其余部分基本没有变化,整个剖面的平均冲刷深度仅为0.04 m;当潮差为4 m时,深槽的平均冲刷深度为1.63 m;当潮差为6 m时,深槽的平均冲刷深度为2.18 m;当潮差在2 ~ 6 m的范围内变动时,潮差每增大1 m,深槽冲刷深度增加0.55 m,说明潮差对深槽冲刷深度有显著影响。这是因为涨潮历时不变,潮差越大,潮流的流速越大,水流的切应力就越大,从而起动的沉积物颗粒越多,冲刷量也越大。

图 3 模拟的深槽剖面演变过程1:初始剖面形态;2:历时0.5 a时的剖面形态;3:历时1.0 a时的剖面形态;4:历时0.5 a,1.5 a时的剖面形态;5:历时0.5 a,2.0 a时的剖面形态;6:历时0.5 a, 2.5 a时的剖面形态;7:历时3.0 a时的剖面形态Fig.3 Modeled evolution of the channel1.the initial profile of the channel; 2.the profile after six months; 3.the profile after one year; 4.the profile after one year and six months; 5.the profile after two years; 6.the profile after two years and six months; 7.the profile after three years.
3.3 初始剖面的坡度对冲刷深度的影响
当模型的其它输入参数不变而只改变初始剖面的坡度时,则运行结果如图5所示,当深槽初始剖面的坡度为0.05%时,均衡态时深槽的平均冲刷深度为4.38 m;当初始剖面的坡度为0.07%时,深槽的平均冲刷深度为2.69 m;当初始剖面的坡度为0.09%时,深槽的平均冲刷深度为1.36 m;当初始剖面的坡度在0.05% ~ 0.09%的范围内变动时,坡度每增大0.01%,深槽的冲刷深度就减小0.76 m,说明初始剖面的坡度对深槽冲刷深度有显著影响,这是因为深槽初始剖面的坡度越大,潮流流速越小,从而起动的沉积物颗粒越少,冲刷量也越小。
4 讨 论
在潮周期内当近底部切应力超过临界切应力时,海底会出现冲刷,则需计算底床上因再悬浮引起的冲刷通量;而当近底部切应力小于临界切应力时,通常底床会出现泥沙落淤。为简单起见,本文忽略因悬沙落淤而引起的底床堆积。可实际上,当潮周期内近底部切应力小于临界切应力时,则悬沙落淤会造成底床的变形。因此实际深槽冲刷达到均衡态的历时要长于本文的计算结果。尽管如此,本项研究表明,底质为细颗粒沉积物的深槽达到均衡态的历时远远短于沙砾质底床的历时[21]。
虽然江苏如东海岸潮流流速较大,表层沉积物较细,沉积物的输运主要以悬移质方式为主,但是本区涨潮历时略大于落潮历时,平均涨潮流速小于平均落潮流速,潮周期内推移质有一定的向海净输运。本项研究只是初步模拟潮流深槽的冲刷演变,故忽略了推移质输运引起的冲淤效应。如模拟更接近自然状态下潮流深槽的冲刷演变则必须考虑潮周期内推移质净输运对深槽冲刷的影响。

图 4 不同潮差作用下深槽的冲刷深度2-0:潮差为2 m时的深槽初始剖面;2-1:剖面2-0对应的均衡态剖面;4-0:潮差为4米时的深槽初始剖面;4-1:剖面4-0对应的均衡态剖面;6-0:潮差为6米时的深槽初始剖面;6-1:剖面6-0对应的均衡态剖面Fig.4 Scour depth of the channel with different tidal ranges2-0: the initial profile of the channel with the tidal range of 2m; 2-1: the equilibrium state of the channel corresponding to the profile of 2-0; 4-0: the initial profile of the channel with the tidal range of 4m; 4-1: the equilibrium state of the channel corresponding to the profile of 4-0; 6-0: the initial profile of the channel with the tidal range of 6m; 6-1: the equilibrium state of the channel corresponding to the profile of 6-0

图 5 不同坡度条件下的深槽冲刷深度1-0:坡度为0.05%时的深槽初始剖面;1-1:剖面1-0对应的均衡态剖面;2-0:坡度为0.07%时的深槽初始剖面;2-1:剖面2-0对应的均衡态剖面;3-0:坡度为0.09%时的深槽初始剖面;3-1:剖面3-0对应的均衡态剖面Fig.5 Scour depth of the channel with different longitudinal seabed slopes1-0: the initial profile of the channel with the obliquity of 0.05%; 1-1: the equilibrium state of the channel corresponding to the profile of 1-0; 2-0: the initial profile of the channel with the obliquity of 0.07%; 2-1: the equilibrium state of the channel corresponding to the profile of 2-0; 3-0: the initial profile of the channel with the obliquity of 0.09%; 3-1: the equilibrium state of the channel associated with the profile 3-0
5 结 论
本文通过模拟江苏如东海岸“倚岸型”潮流沙脊体系中的深槽冲刷过程中剖面的变化得出如下结论:(1)根据给定初始剖面的坡度、潮差等参数,可以通过一维模拟得出深槽达到均衡态的历时,如东海岸潮流沙脊体系中的深槽达到均衡态的历时为2.5 a;(2)若给定初始剖面的坡度,则潮差越大,达到均衡态时深槽的冲刷深度越大且潮差的变化对冲刷深度有显著影响;(3)若给定潮差,则初始剖面的坡度越大,均衡态时深槽的冲刷深度越小且坡度的变化对深槽冲刷深度有显著影响。模拟结果表明,深槽在冲刷过程中存在着均衡态,潮差和初始剖面的坡度是深槽冲刷深度的主要控制因素。
[1]Off T.Rhythmic linear sand bodies caused by tidal currents [J].Bulletin of the American Association for Petroleum Geologists, 1963, 47: 324-341.
[2]Huthance J M.On one mechanism forming linear sand banks [J].Estuarine, Coastal and Shelf Science, 1982a, 14: 79-99.
[3]Huthance J M.On the formation of sand banks of finite extent [J].Estuarine, Coastal and Shelf Science, 1982b, 15: 277-299.
[4]Collins M B, Shimwell S J, Gao S, et al.Water and sediment movement in the vicinity of linear sandbank: the Norfolk Banks, southern North Sea [J].Marine Geology, 1995, 123: 125-142.
[5]Williams J J.Offshore sand bank dynamics [J].Journal of Marine Systems, 2000, 24: 153-173.
[6]任美锷.江苏省海岸带和海涂资源综合调查报告 [M].北京: 海洋出版社, 1986.
[7]王颖.黄海陆架辐射沙脊群 [M].北京: 中国环境科学出版社, 2002.
[8]张东生, 张君伦.黄海海底辐射沙洲区的M2潮波 [J].河海大学学报, 1996, 24(5): 35-40.
[9]张东生, 张君伦, 张长宽, 等.潮流塑造-风暴破坏-潮流恢复—试译黄海海底辐射沙脊群形成演变的动力机制 [J].中国科学(D辑), 1998, 28(5): 394-402.
[10]王建, 闾国年, 林珲, 等.江苏岸外潮流沙脊群形成的过程与机制 [J].南京师大学报(自然科学版), 1998, 21(3): 95-108.
[11]诸裕良, 严以新, 薛鸿超.南黄海辐射沙洲形成发育水动力机制研究---I.潮流运动平面特征 [J].中国科学(D辑), 1998, 28(5): 403-410.
[12]汤毓祥, 刘振夏, 姚兰芳.渤海M2潮流及其与辽东浅滩潮流脊发育的关系 [J].海洋通报, 1994, 13(1): 25-30.
[13]李海宇, 王颖.GIS与遥感支持下的南黄海辐射沙脊群现代演变趋势分析 [J].海洋科学, 2002, 26(9): 61-65.
[14]刘振夏, 夏东兴.潮流沙脊的水力学问题探讨 [J].黄渤海海洋, 1995, 13(4): 23-29.
[15]陈君, 王义刚, 张忍顺, 等.江苏岸外辐射沙脊群东沙稳定性研究 [J].海洋工程, 2007, 25(1): 105-113.
[16]朱大奎, 龚文平.江苏岸外海底沙脊群西洋深槽的稳定性分析[J].海洋通报, 1994, 13(5), 36-43.
[17]吴德安, 张忍顺.江苏辐射沙洲陈家坞悬沙变化过程及垂线分布资料分析 [J].泥沙研究, 2007(2): 42-48.
[18]Partheniades E.Erosion and deposition of cohesive soil [J].Journal of the Hydraulics Division,1965, ASCE, 91(HY1): 105-139.
[19]Wang Y P, Gao S, Ke X K.Observations of boundary layer parameters and suspended sediment transport over the intertidal flats of northern Jiangsu, China [J].Acta Oceanologica Sinica, 2004, 23(3): 437-448.
[20]Dyer K R.Coastal and estuarine sediment dynamics [M].Chichester: John Wiley, 1986: 342.
[21]Xie D F, Gao S, Wang Y P.Morphodynamic modelling of open-sea tidal channels eroded into a sandy seabed [J].Geo-Marine Letters, 2008, 28(4): 255-263.
Modeling channel scour associated with shore-attached tidal ridges: A case study from Rudong coast, Jiangsu Province
LIU Xiu-juan1, GAO Shu2, WANG Ya-ping2
(1.Faculty of Earth Resources, China University of Geosciences, Wuhan 430074, China;2.Key Laboratory for Coast and Island Development of the Ministry of Education, Nanjing University, Nanjing 210093, China)
The tidal ridges off the Rudong coast, Jiangsu Province, are a part of the radial tidal ridge system of the southern Yellow Sea.These ridges and the inter-ridge channels represent a kind of shore-attached tidal ridge systems.In this contribution, the evolution from an initial profile to morphodynamic equilibrium was simulated with a horizontal 1-D model.Numerical experiments were carried out for different tidal ranges and longitudinal bed slopes, to evaluate their influence on the equilibrium state of the channel morphology.The results show that: (1) The channel will reach equilibrium during a certain period of time, if the initial profile of the channel and tidal range are known; (2) with an invariable initial profile of the channel, as the tidal range increases, the equilibrium scour depth of the channel also increases, indicating that tidal range has a significant influence on the scour depth; (3) with an invariable tidal range, as the longitudinal bed slope of the channel increases, the scour depth decreases, indicating that the bed slope also affects the final equilibrium state.
shore-attached tidal ridges; equilibrium depth; tidal range; numerical modeling; Jiangsu coast (China)
P737.1
A
1001-6932(2010)03-0271-06
2008-12-05;
2009-11-02
国家自然科学基金项目(No.40876045, 40576040); 国土资源部海洋油气资源与环境地质重点实验室开放基金项目(MRE200906)
刘秀娟 (1972-), 女, 副教授, 研究方向为海岸沉积动力学。电子邮箱:xjliu@cug.edu.cn
