Mellor-Yamada模型在波浪边界层中的运用
2010-09-05陈杰蒋昌波刘虎英邓斌
陈杰,蒋昌波,刘虎英,邓斌
(1. 长沙理工大学水利工程学院,湖南 长沙 410004;2. 湖南省水沙科学与水灾害防治重点实验室,湖南 长沙 410004;3. 湖南省交通规划勘查设计院,湖南 长沙 410008)
Mellor-Yamada模型在波浪边界层中的运用
陈杰1,2,蒋昌波1,2,刘虎英1,3,邓斌1
(1. 长沙理工大学水利工程学院,湖南 长沙 410004;2. 湖南省水沙科学与水灾害防治重点实验室,湖南 长沙 410004;3. 湖南省交通规划勘查设计院,湖南 长沙 410008)
利用Mellor-Yamada 2.5阶封闭格式建立一维垂线波浪边界层数学模型,利用有限元方法求解,模拟线性波作用下的层流边界层和乔治沙洲南侧海岸一侧点的波浪边界层流速分布,并同理论或其他的计算方法进行比较,结果显示该模型具有较高的精度,能广泛运用于波浪边界层的研究中。
Mellor-Yamada模型;边界层;数值模拟
波浪边界层存在于海底床面附近,虽然厚度只有2~10 cm,但其水流运动特性与波浪的传播和变形、泥沙起动以及床面形态的变化密切相关,流体内部紊动结构、波浪底部摩阻力、波浪的质量输移速度、波能衰减、波浪要素变化、波浪作用下的底沙起动输移、悬沙分布及其输送的合理确定等,都直接或间接的与波浪作用下的底部边界层有关。自Jonsson[1]和Sleath[2]的工作以来,人们已经进行了很多关于波浪边界层的理论、数值和实验方面的研究工作。如赵子丹[3]等将大涡模拟法简化为二维形式,利用SGS格子涡模型封闭二维Navier-Storkes方程水流运动方程组,得到平底振荡流边界层立面二维水流数值模型,讨论了振荡流边界的紊动特性沿垂线分布和随相位变化的情况。蒋昌波[4]等建立了立面二维曲线坐标下的数值模型,模拟波浪作用下底层分离涡随时间、空间变化的动力特性,对底层流动的紊动特性、床面剪切应力的随时间、空间的变化以及涡动结构的尺度分别进行了讨论。孙亚斌[5]等利用格子Boltzmann方法中不可压缩的模型模拟了线性波和椭圆余弦波作用下的层流边界层流速变化情况,程永舟[6,7]等研究了椭圆余弦波作用下的非对称沙纹上的流动特性。然而,由于波浪边界层的复杂性,波浪边界层的问题仍然需要深入研究。
Mellor和Yamada[8,9]提出一种层次化的封闭模型,即Mellor-Yamada模型(以下简称MY模型)。Mellor-Yamada模型用紊动能量(Turbulent energy)和紊动特征长度(Turbulent length scale)参数表示,共分成了5个等级。MY模型的优点是使用很少的封闭所需常数。MY模型已经广泛的运用与大气[10,11]和海洋[12-14]的计算。许多学者对MY模型进行改进、推广和运用。万振文[15]等将MY闭合模型推广应用到生态动力学模型方程的二阶湍封闭过程中。李华军[16]等探讨Mellor-Yamada模型考虑泥沙的影响,进而再将其用于河口地区泥沙输移的探索和研究。本文将MY模型运用于波浪边界层问题的研究,建立利用Mellor-Yamada 2.5阶封闭模型的一维垂线边界层数学模型,并用于波浪边界层问题的研究。
1 模型基本理论
1.1 基本方程
一维垂线边界层数学模型的基本方程为符合传统静力学假设的浅水方程。动量守恒方程和能量守恒方程中的雷诺湍动和通量项都用参数化的涡扩散率表示,动量方程中考虑科氏力的作用,水平变量和垂直面水平对流忽略不计。
连续方程为:

动量方程为:
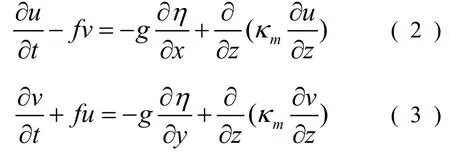
能量守恒方程为:
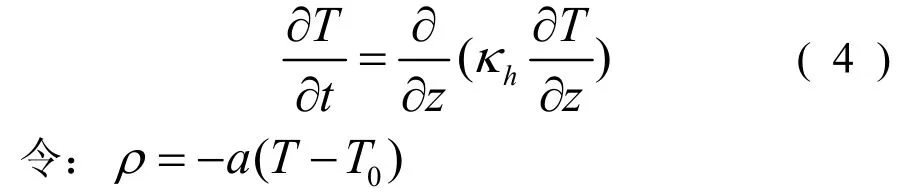
则能量守恒方程可以写成:
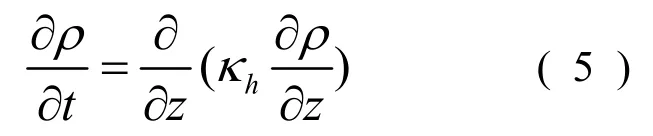
1.2 边界条件
在自由边界,使用风压力wτ和热流通量˙H都源于水平动量和能量,分别为:
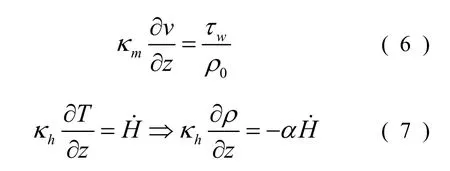
在底部边界,假设剪应力τb为常数,摩阻流速u*与剪应力的关系为:

则对数流速分布为:
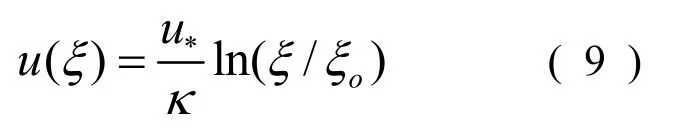
底部滑移条件时,定点速度用剪应力粗糙高度表示:

由 (8)(9)(10) 式得到阻力系数:
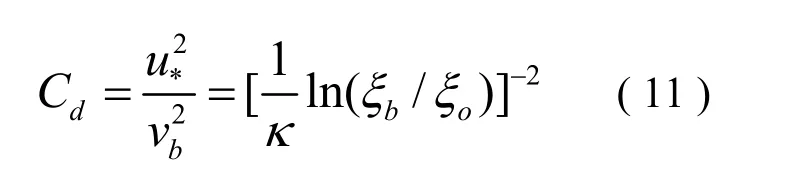
因此得到:
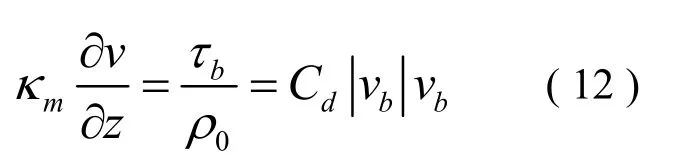
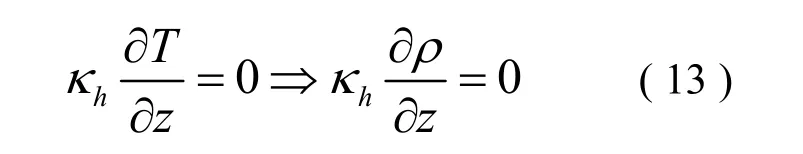
在自由水面,紊动能量与紊动特征长度有:
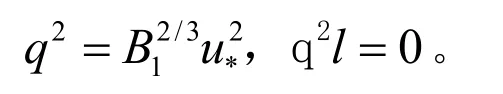
1.3 Mellor-Yamada 2.5阶封闭模型
Mellor-Yamada 2.5阶封闭模型将紊动动能(turbulent kinetic energy)和紊动特征长度(turbulent master length scale)引入守恒方程。尽管计算引入参数,但是考虑到这些参数的瞬时性和空间演变性,因此其具有很多优点。Mellor和Yamada[9]将守恒方程写成紊动动能和紊动特征长度的形式:
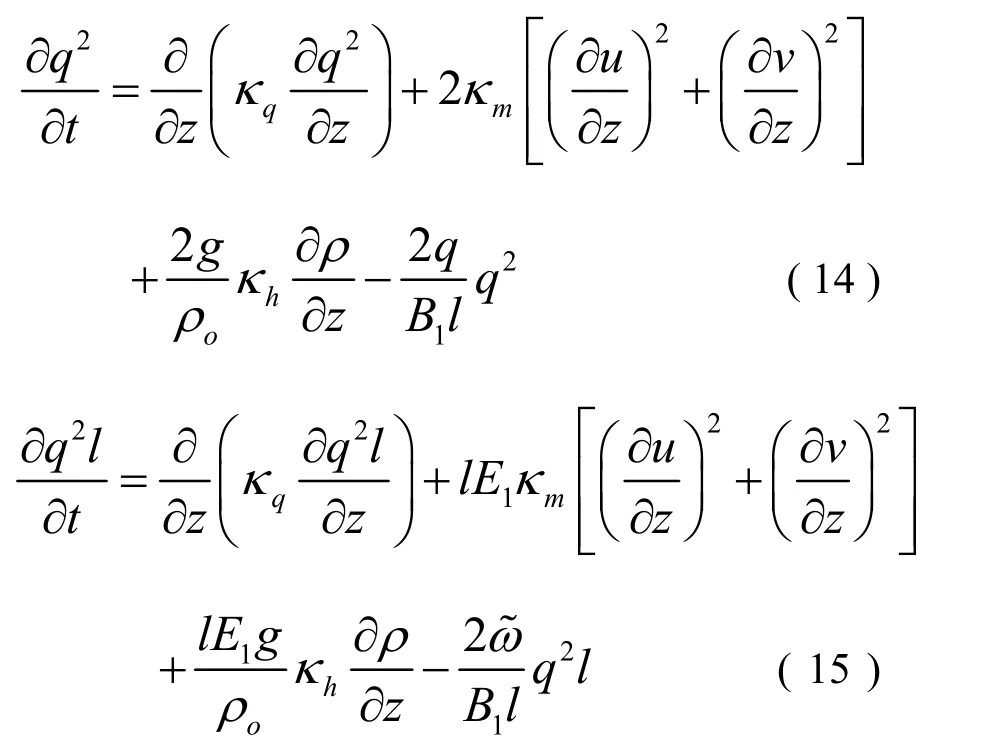
紊动粘性系数mκ,紊动扩散系数hκ,紊动量扩散系数qκ的确定如下式:

式中,E1,E2分别取1.8,1.33;A1,B1,A2,B2,C1,Sq,S1是与主控的紊动特征长度和紊动结构特征有关的实验常数,分别取0.92,16.6,0.74,10.1,0.08,0.2,0.2。
1.4 数值方法
模型采用有限元方法进行求解,利用均匀网格进行离散。
2 模型运用及结果讨论
2.1 线性波作用下的层流边界层
层流边界层内的流体运动方程为:
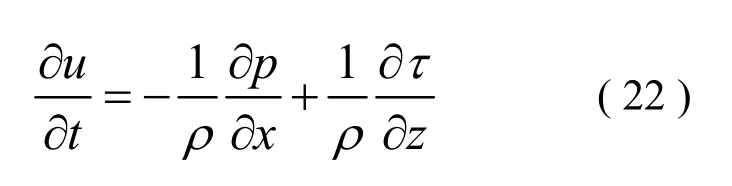
式中:u为边界层内任一点的流速,p为边界层内任一点的压力, 为边界层内任一点的剪切应力。
由微幅波理论,近底质点水平速度为:
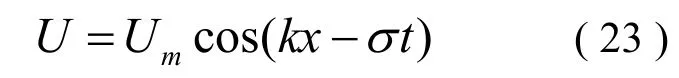
式中,Um是近底波浪水质点水平速度的最大值,k是波数,ω是波浪角频率
于是线性波作用下边界层内任一点流速为:
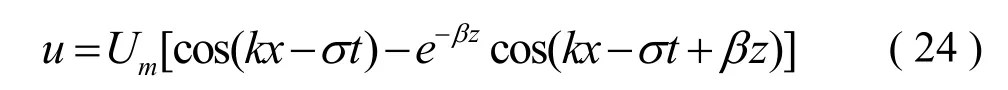
图1给出的线性波(波高0.10 m,周期1.6 s,水深0.40 m)作用下一个周期内床面附近的水平流速分布的数值模拟结果和理论值,横轴坐标为u/ Um,纵轴坐标为z/δ,两个都是无量纲的量,δ为朗吉特-希金斯定义的边界层厚度其中,实线为理论值,圆点为数值模拟值。可以看出数值模拟结果十分逼近理论结果。特别是在t0, ,2π附近,也就是边界层流速达到最大值时,两个结果吻合良好。在tπ/2和3π/2附近,在靠近海床的地方数值模拟值略小于理论值,两者最大误差在5%以内。运用朗吉特-希金斯定义的边界层厚度求得理论边界层厚度δ为0.713 6 mm,将数值模拟结果运用Jonsson[1]提出的方法求得边界层厚度d为0.709 5 mm,误差为0.6%。因此,该模型能很好的运用于线性波作用下层流边界层流场问题的研究,且具有较高的精度。
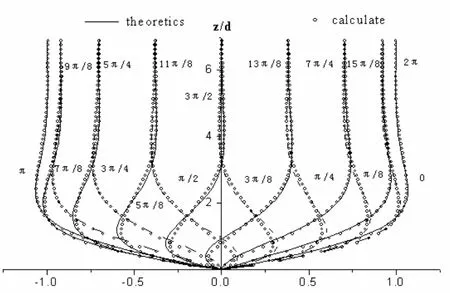
图1 线性波作用下层流边界层流速分布Fig. 1 Velocity distributions in laminar flow under linear wave
2.2 乔治沙洲海岸波浪边界层
图2给出乔治沙洲南侧海岸一侧点的波浪边界层流速分布,海岸受到M2潮汐和0.095 5 Pa风的作用,风向为偏北118.5°[17]。设u方向为正北方向,横轴为流速,纵轴为水深,实线为Mellor-Yamada方法计算值,圆点为Davies和Furnes[18]提出二次涡粘性封闭格式(Quadratic Eddy Viscosity Closure)的计算值。可以看出两者计算结果比较接近,因此,该模型能很好的运用于波浪作用下边界层流场问题的研究,且具有较高的精度。
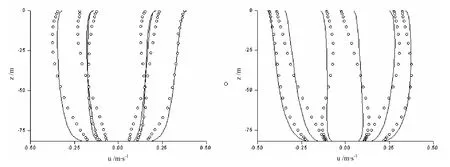
图2 乔治沙洲海岸波浪边界层流速分布Fig. 2 Velocity distributions on the southern flank of Georges Bank
3 结 论
本文引进Mellor-Yamada 2.5阶封闭格式建立一维垂线波浪边界层数学模型,利用有限元法进行求解,模拟线性波作用下的层流边界层,并同理论值进行比较,模拟乔治沙洲南侧海岸一侧点的波浪边界层流速分布,并且同其他学者提出的计算方法进行比较,结果显示该一维垂线数学模型具有较高的精度。
同时,由于实际海洋环境中波浪作用是随机的,因此利用该数学模型模拟随机波浪作用下的边界层流动结构更加具有实际意义,将成为我们下一步工作的重点。本文认为Mellor-Yamada封闭格式具有使用很少的封闭常数,计算快捷、准确等优点,在波浪边界层及海岸泥沙运动机理等问题的研究中将得到广泛的运用。
[1] Jounsson I G. Wave boundary layer and friction factor [J]. Proc 10th Conf Coastal Eng ASCE Tokyo, 1966: 127-148.
[2] Sleath J F A. Velocities above rough bed in oscillatory flow [J].Water, Port Coastal Ocean Eng, 1974, 100(WW4): 287-304.
[3] 赵子丹, 蒋昌波, 白玉川. 振荡流底部边界层运动的数值研究[J]. 天津大学学报, 2001, 34(5): 568-572.
[4] 蒋昌波, 白玉川, 赵子丹, 等. 波浪作用下沙纹床面底层流动特性研究 [J]. 水科学进展, 2003, 14(3): 332-340.
[5] 孙亚斌, 张庆河, 张金凤. 振荡层流边界层运动的格子Boltzmann模拟 [J]. 水动力学研究与进展, 2006 (5): 347-353.
[6] Cheng Yongzhou, Wang Yongxue, Jiang Changbo. An experimental investigation of the velocity under cnoidal waves over the asymmetric rippled bed [J]. Acta Oceanologica Sinica, 2007, 26 (1):130-139.
[7] 程永舟, 王永学, 蒋昌波, 等. 浅水非线性波作用下沙纹床面底层流动特性试验研究 [J]. 水科学进展, 2007, 18(6): 801-806.
[8] Mellor G, Yamada Y. A hierarchy of turbulence closure models for planetary boundary layers [J]. Journal of the Atmospheric Sciences,1974, 31(10): 1 791-1 806.
[9] Mellor G, Yamada Y. Development of a turbulence closure model for geophysical fluid problems [J]. Reviews of Geophysics and Space Physics, 1982, 20(4): 851-875.
[10] Yamada T. Anumerical experiment on pollutant dispersion in a horizontally-homogeneous atmospheric boundary layer Atmos [J].Environ, 1977, 11: 1 015-1 024.
[11] Yamada T, Bunker S. Anumerical model study of nocturnal drainage flows with strong wind and temperature gradients [J]. Appl Meteorol, 1989, 20: 545-554.
[12] Kantha L H, Clayson C A. An improved mixed layer model for geophysical applications [J]. J Geophys Res, 1994, 99: 25 235-25 266.
[13] Mellor G L. One-dimensional, ocean surface layer modeling: a problem and a solution [J]. J Phys Oceanogr, 2001, 31: 790-809.
[14] 魏皓, 武建平, 张平. 海洋湍流模式应用研究 [J]. 青岛海洋大学学报, 2001, 31(1): 7-13.
[15] 万振文, 袁业立. 海洋浮游生态系统连续介质动力学模型湍封闭研究 [J]. 水动力学研究与进展, 2001, 15(2): 229-239.
[16] 李华军, 梁丙臣, 李东永, 等. 悬对沙Mellor-Yamada海洋边界层模型计算结果的影响 [J]. Marine Sciences, 2004, 28(1): 27-32.
[17] Naimie C E, Loder J W, Lynch D R. Seasonal variation of the three-dimensional residual circulation on Georges Bank [J].Geophys Res, 1994, 99(C8): 15 967-15 989.
[18] Davies A M, Furnes G K. Observed and computed M2 tidal currents in the North Sea [J]. Phys Oceanogr, 1980, 10: 237-257.
Study of wave boundary layer based on Mellor-Yamada model
CHEN Jie1,2, JIANG Chang-bo1,2, LIU Hu-ying1,3, Deng Bin1
(1. School of Water Conservancy, Changsha University of Science & Technology, Changsha 410114, China;2. Hunan Province Key Laboratory of Water, Sediment Sciences & Flood Hazard Prevention, Changsha 410114, China;3. Hunan Provincial Communications Planning, Survey & Design Institute, Changsha 410008, China)
The one dimension time-stepping point numerical model which uses linear finite elements to determine the vertical structure of the horizontal components of velocity under wave forcing is given. And the velocity distributions in laminar flow under linear wave and on the southern flank of Georges Bank are presented. Compared with theoretic and other numerical models, the numerical result shows result is good and that the numerical model is able to investigate the wave boundary layer problem.
Mellor-Yamada model; wave boundary layer; numerical simulation
P731.22; TV139.2
A
1001-6932(2010)03-0253-04
2008-12-08;收订日期:2009-10-30
国家自然科学基金资助项目(No.50979008,50909009),水沙科学与水灾害防治湖南省重点实验室基金资助
陈杰(1982-),男,助教,博士生,主要从事河流、海岸动力过程及其模拟技术的研究。电子邮箱:chenjie166@yahoo.com.cn
