电镀层均匀性的数值模拟及验证

刘太权

(华南理工大学,广东 广州 510640）

电镀层均匀性的数值模拟及验证

刘太权

(华南理工大学,广东 广州 510640）

采用数值模拟的方法,对电镀中电流密度的变化进行模拟,预测了镀层厚度变化的趋势,解释了这些变化产生的原因。并通过实验研究取样及在扫描电镜下对微观组织的观察,对模拟结果进行了进一步的验证。

电镀;数值模拟;电流密度;实验分析

0 前言

电镀技术由于其特殊优点被广泛应用于汽车、航空、电子等诸多行业[1]。微机电系统(MEMS）的发展给传统电镀技术带来了新的活力,促进了整个电镀行业的发展[2-3]。然而,电镀技术在MEMS领域中也遇到了一些新的难题,如:镀层内应力控制问题、掩膜电沉积厚度均匀性问题、叠层结构层间结合力问题、高深宽比孔洞填充问题[4-5]等,限制了电镀技术的应用,因此,这些技术问题亟需解决。

本研究以电化学镀层为研究对象,采用数值模拟的方法,分析了电镀过程中阴、阳两极板间电场的大小及分布的均匀性,预测了镀层厚度的变化。并通过对实际电镀样品取样及微观组织观察,对模拟结果进行了验证。

1 数学原理

当电流通过电解液时,阴极表面沉积的镀层的体积,按照Faraday定律计算:

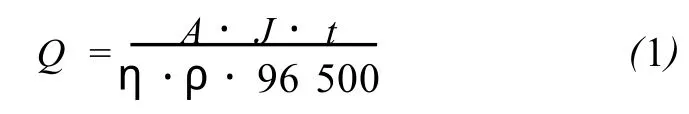
式中:Q为沉积体积,mm3;A为沉积元素的相对原子量;η为沉积元素的原子价;ρ为沉积元素的密度,g/mm3;J为电流密度,A/m2;t为时间,s。

当阳极和阴极工作表面距离为 y,阴、阳极板间电压为V,电流密度可以由下式给出:

式中:k为电阻率,V·mm-1。

根据(1）式和(2）式,综合可得下式:

式中:D为镀层厚度,mm。

理论上,由于极板间距离相比镀层厚度较大,电镀过程中各位置的电流密度将保持不变。然而,实际生产中,由于电流密度在工作表面上并不相同,且在工作表面上分布复杂,因此,建立与实际情况相似的几何模型,并通过数值模拟的方法来研究此种变化就显得尤为重要[6]。

2 模拟结果与分析

2.1 几何模型的建立与计算参数设置

由于3D模型相比2D模型更接近实际生产情况,因此,在Ansys中采用3D模型来进行模拟计算。图1所示为电解槽中阴、阳两极板及绝缘挡板的三维模型。实验分4组模型,A组:无挡板,阴、阳两极板间距离为30 mm;B组:有挡板,阴、阳两极板距离为30 mm;C组:无挡板,阴、阳两极板距离为60 mm;D组:有挡板,阴、阳两极板距离为60 mm。

模拟中绝缘挡板处于阴、阳两极板的中间,且到两极板的距离相等,各组中阴、阳两极板、绝缘挡板以及挡板上的方孔大小均相等。其中,绝缘板上的方孔小于阴、阳两极板。挡板的主要作用是解决镀层厚度不均匀的问题,通过挡板上的方孔对溶液中电力线的收束作用,使得阴极表面的电场分布趋于均匀。阳极板为铂材料,阴极板为铜材料,挡板和衬底均为电阻率无穷大的绝缘材料。

将图1的三维图形在pro/e中生成STL格式,导入ansys模拟软件,进行参数设置及网格剖分。模拟中单元类型采用SOLID 231,材料电阻率参数,如表1所示。

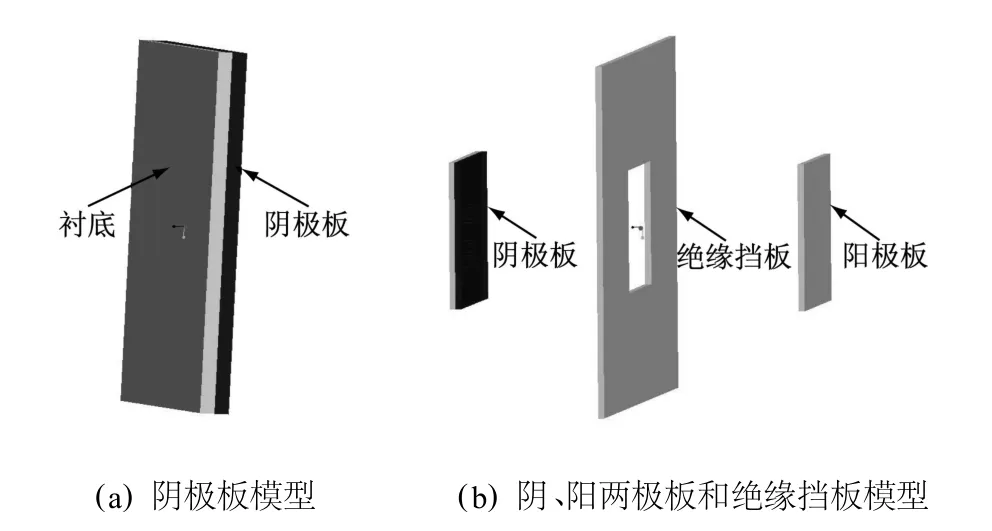
图1 模拟三维造型图

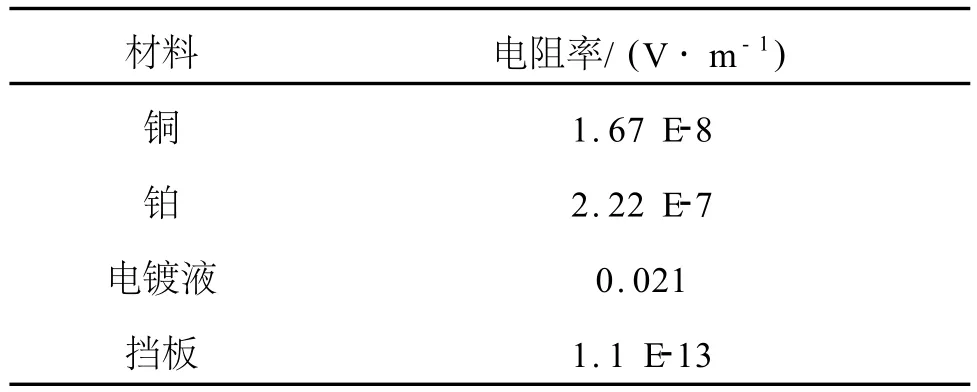
表1 材料电阻率参数

定义好材料属性后,对模型进行网格剖分。由于实验中起主要作用的为挡板和极板,因此,为了获取更好的观察结果及提高计算效率,挡板和极板要进行网格细划分处理,其余部分网格尺寸相对较大,剖分结果,如图2所示。电镀中阳极板所加载的电压为6 V,阴极板的电压为0 V。同时在电镀液表面定义边界条件,即:外部电压全部为0 V,开始进行模拟计算。

图2 网格剖分结果

2.2 模拟结果分析及讨论

由公式(3）可知:电镀层厚度和电流密度成正比,因此,在阴极板上取一条水平路径,通过这个路径上电流密度的变化来定性评价电镀层厚度分布的基本规律。图3为各组模型中电流密度的数值模拟变化结果。

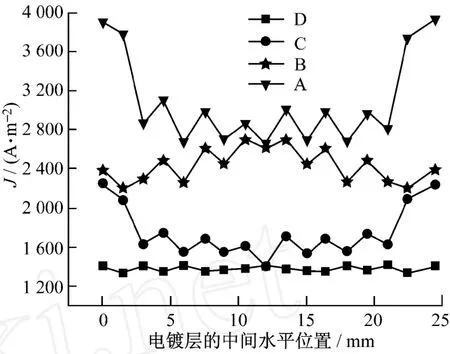
图3 各组模型中电流密度的数值模拟变化结果

由图3可知:不加挡板时(A组、C组）,阴极板工作表面中间位置的镀层厚度明显低于边缘位置。这是由于电场线通过 x,y,z3个方向传递,在阴极板工作表面的边缘聚集较多,而在中间部位聚集则相对较少,从而使阴极板工作表面镀层的边缘厚度大于中间部位的厚度。加挡板时(B组、D组）,镀层厚度趋向均匀。这是因为绝缘挡板上方孔对电场线的收束作用,使得阴极表面的电场线分布均匀。但B组中,由于挡板离阴极板距离很近,镀层厚度在中间位置有所增加。此外,A组和B组的镀层厚度要显著高于C组和D组的。由公式(2）可知:在阴、阳极板间电压不变的情况下,随着挡板离阴极板距离的增加,电流密度减小,从而使得电镀层厚度呈减小趋势。

3 实验分析

3.1 电镀层厚度分析

为了验证模拟的有效性,对A,B,C和D 4组模型分别进行了电镀实验。实验中的材料及工艺参数为:阳极材料 铂片,阴极材料 铜片,电流密度0.64～5.76 A/dm2,占空比 40%,脉冲频率 500 Hz,5 min,25°C;电沉积采用赫尔槽实验,溶液组成为:硫酸亚锡、硫酸铋、硫酸、配位剂,电镀电源采用脉冲电源。

电镀完成后,样品经水洗烘干后,采用德国产durlscope mpor测厚仪测量试片各点厚度。图4为各组实际样品的厚度变化曲线。由图4可以看出:无挡板时,由于边缘效应,阴极板边缘电镀层厚度大于中间厚度,A组和C组均呈现很明显的中间凹下,周围凸起的趋势。加挡板时,B组和D组电镀层厚度波动范围均变小。对于B组的情况,由于挡板孔径较小,离阴极板的距离又很近,镀层的中间位置出现了很明显的凸起;而D组电镀层厚度相对较均匀,这些与模拟结果是基本吻合的。

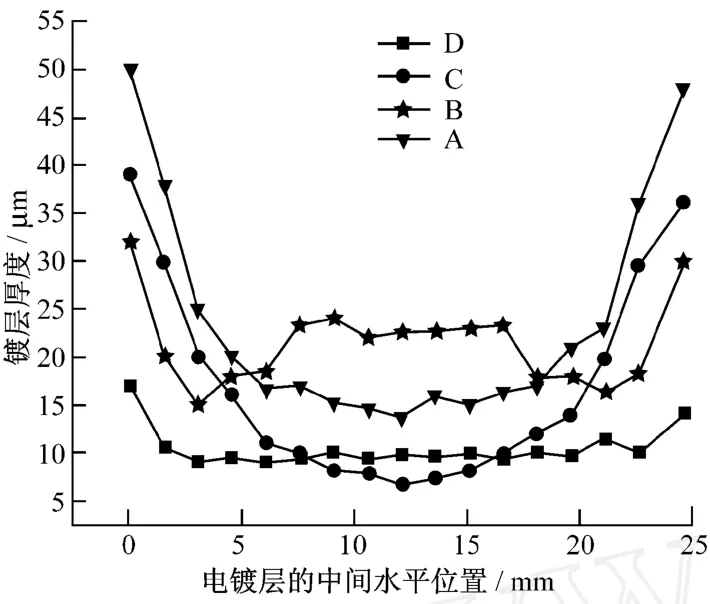
图4 各组实际样品的厚度变化曲线

3.2 镀层表面微观形貌

图4是通过在试片上从左到右取点的办法得到的厚度变化曲线。由于在电镀过程中,低电流密度区和高电流密度区通常都难以上镀,因此,取点的方法只能表述一个总的镀层厚度变化趋势。为了进一步验证模拟结果,采用S-3 700型扫描电子显微镜(SEM）观察各组镀层的表面微观形貌。实验结果,如图5所示。

图5 各组镀层的表面微观形貌

从图5可以明显看出:A组镀层表面高低不平,白色矩形框内的区域厚度较大,而其他区域相对较小,存在较大的空洞;B组镀层形貌趋向均匀,但仍存在一些较小的空洞,如图中白色箭头所指区域;C组表面镀层厚度不均匀,存在较大的空洞,白色椭圆框区域内的阴极板工作表面没有被镀层覆盖;D组表面形貌较平整,镀层厚度均匀。

上述分析表明:实验结果与模拟结果基本吻合。采用ansys模拟分析对于改善电流分布的均匀性有一定的指导意义。但由于模拟是在理想的情况下进行的,只考虑了几何的因素,而实际电镀中,诸如:电镀液的浓度的变化等电化学方面的因素在模拟中没有考虑。因此,模拟中得到的较好的优化条件,需要在实际生产中做进一步的调整,根据实验结果进一步修改电镀模型。

4 结论

(1）通过对电镀过程的数值模拟及实验分析表明:数值模拟能够有效地预测镀层厚度变化趋势,可为实际生产及成熟工艺优化提供参考。

(2）绝缘挡板的施加,在一定程度上,可以使电镀层更加均匀和平整。此外,随着极板间距离的增大,镀层厚度呈减小趋势,降低了电镀效率。

[1] Suganuma K.Advances in lead-free electronics soldering[J].Current Opinion in Solid State and Material Science,2001,5(1）:55-64.

[2] Deconinck J,Maggetto G,Vereecken J.Calculation of current distribution and electrode shape change by the boundary element method[J].Journal of Electrochemical Society,1985,132(12）:2 960-2 965.

[3] Prentice G A,Tobias C W.A survey of numerical methods and solutions for current distribution problems[J].Journal of Electrochemical Society,1982,129(1）:72-78.

[4] Luo J K,Chu D P,Flewitt A J,et al.Uniformity control of Ni thin-film microstructures deposited by through-mask plating[J].Journal of Electrochemical Society,2005,152(1）:C36-C41.

[5] Toshikazu O,Tamie K,Kazyo K.Patterned copper plating layer thickness made uniform by placement auxiliary grid electrode about ball GRID arrays[J].Chemical Engineering Communications,2006,193:1 503-1 513.

[6] 孙明礼,胡仁喜,崔海蓉,等.ansys10.0电磁学有限元分析[M].北京:机械工业出版社,2007.

Numerical Simulation and Verification on the Uniformity of Electroplated Coating

LIU Tai-quan
(South China University of Technology,Guangzhou 510640,China）

The changes of current density in electroplating were simulated numerically;thickness of the electroplated coating was predicted and the reasons for these changes are given.The simulative results were further verified by observing microstructure of the experimental samples with SEM.

electroplating;numerical simulation;current density;experimental analysis

TQ 153

A

1000-4742(2010）02-0011-03

广州市科技计划项目(2008A1-D0011）

2009-08-05