深海采矿车的轨迹跟踪控制算法与仿真
2010-12-27王随平张海宁李闪阁
王随平,张海宁,李闪阁
(中南大学信息科学与工程学院,长沙410083)
深海采矿车的轨迹跟踪控制算法与仿真
王随平,张海宁,李闪阁
(中南大学信息科学与工程学院,长沙410083)
根据深海采矿车的运动学模型,考虑随机打滑率等干扰影响,采用分层控制的思想将采矿车的轨迹跟踪控制分为2部分:轨迹跟踪模糊控制器和速度PID控制器.基于连续状态反馈的有限时间控制算法,结合模糊逻辑控制器,设计了一种连续的状态反馈轨迹跟踪控制算法,仿真结果表明了该方法的有效性.
深海采矿车;轨迹跟踪;分层控制;有限时间
海底采矿车的智能控制是深海采矿系统的关键技术,采矿车在行驶过程中极易打滑,压陷较深,难以按预定开采路径行走,对深海采矿产生了直接的影响[1].目前深海开采策略的实现只能根据来自海底的测试数据,如海底采矿车左右履带行走速度、车体速度、方位角等,采用智能控制方法,控制海底采矿车行走液压系统左右履带速度,以期达到车体以预定行走速度按预定开采路径来开采深海矿石的目的[2].
本文采用分层控制的思想,基于连续状态反馈的有限时间控制算法,结合模糊逻辑控制器和速度PID控制器,设计一种连续的状态反馈轨迹跟踪控制算法,这对海底采矿技术有一定的现实意义.
1 模型分析
1.1 采矿车运动学模型
海底采矿车坐标系为oxy,转向运动瞬时中心为点M,海底采矿车运动学模型如图1所示.

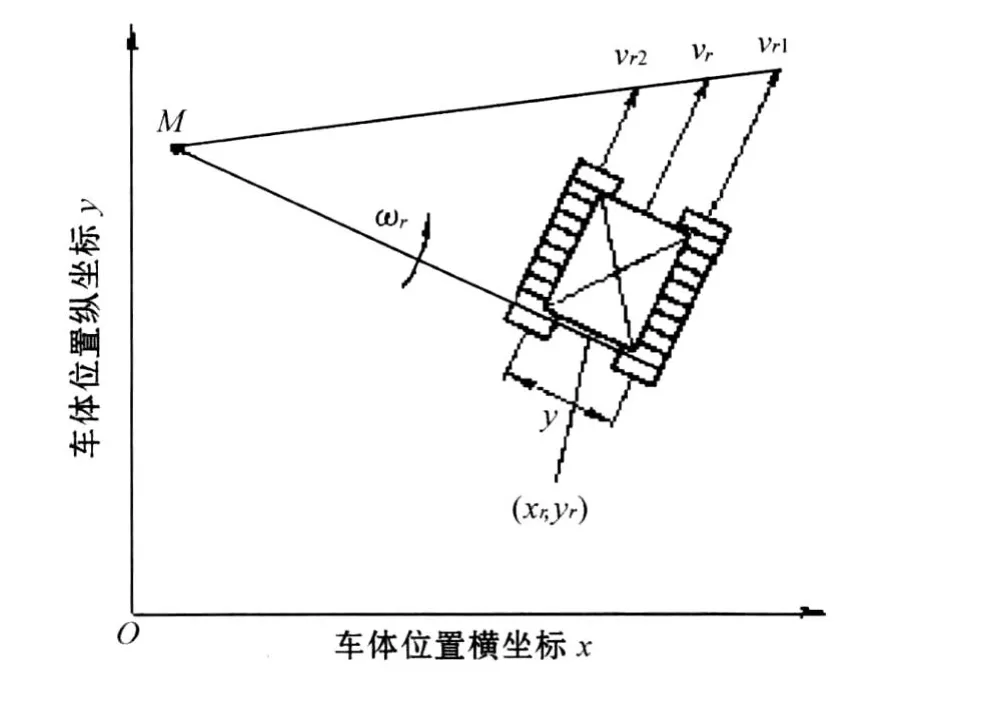
图1 海底采矿车运动学模型
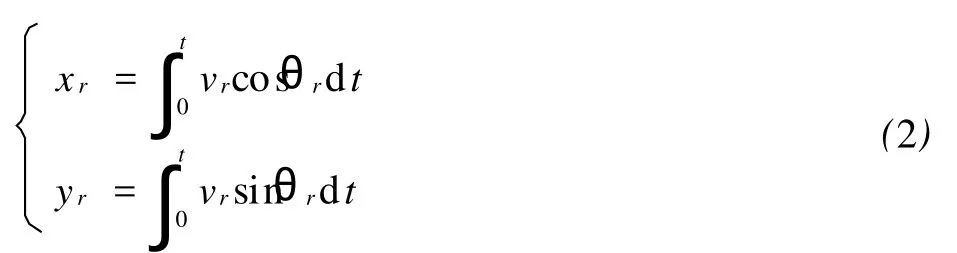
式中:vr为车体实际速度;ωr、θr分别为车体实际行走角速度和方位角;s为左右履带中心距;vr2、vr1分别为左右履带实际行走速度;(xr,yr)为车体实际位置坐标.
在非线性海底复杂阻尼耦合作用下,海底机器人左右履带极易打滑,且左右履带打滑率不同,其左右履带实际速度为:

式中:i1为右履带打滑率;i2为左履带打滑率.
1.2 采矿车动力学模型
采矿车动力学特性由下列方程描述:

式中:v、ω分别为采矿车的平移速度和角速度;(x,y)为采矿车质心的笛卡尔坐标;θ为采矿车前进方向与x轴的夹角.
坐标误差为:
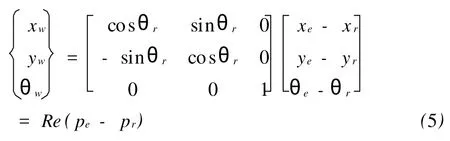
Re为转移矩阵,对上式求导即可导出位姿坐标误差模型:
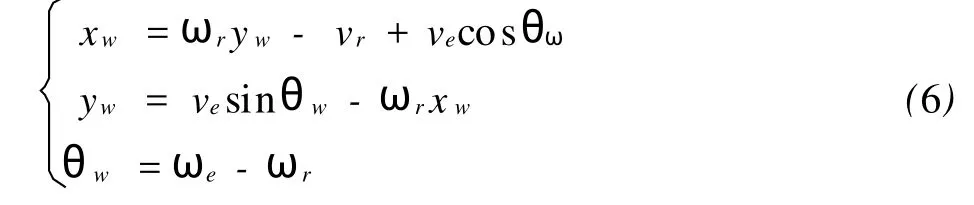
式中:pe=(xe,ye,θe)T为期望位姿坐标;pr=(xr,yr,θr)T为实际位姿坐标;pw=(xw,yw,θw)T为误差位姿坐标[3].
2 控制算法的设计
考虑采矿车在海底受到复杂阻尼耦合作用及液压驱动等动态特性的影响,为了使采矿车实时完成轨迹跟踪,采用分层控制的思想,将采矿车的轨迹跟踪控制分为2层:轨迹跟踪模糊控制器和PID速度控制器.采矿车轨迹跟踪控制系统结构如图2所示.上层轨迹跟踪控制器根据系统位姿误差,经过系统处理得到采矿车2个液压驱动系统的实际执行速度.底层为了使液压系统准确、快速执行响应速度,对2个液压模块分别采用PID控制器进行速度控制.
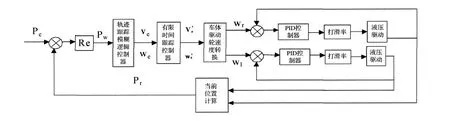
图2 采矿车轨迹跟踪系统结构图
2.1 轨迹跟踪模糊逻辑控制器
根据采矿车的路径偏差e(l)和方位角偏差e(θ)来确定下一步的期望角速度ωe,控制规则如下所述:
(1)如果采矿车路径偏差和方向角偏差均很大,且行走方向远离预定路径,则控制角速度很大,保证其快速转向,以减小路径和方位角偏差;
(2)如果采矿车路径偏差和方向角偏差均很大,且行走方向接近预定运动轨迹,则控制角速度很小,保证采矿车直线行走,迅速接近预定路径;
(3)如果采矿车路径偏差很小,而方向角偏差很大,或者路径偏差很大,而方位角偏差很小,则车体角速度较小或为中等,保证采矿车平滑地接近预定路径;
(4)角速度方向由路径偏差和角速度偏差的符号决定.
根据以上推理规则,海底采矿车相应的模糊逻辑推理如表1所示.
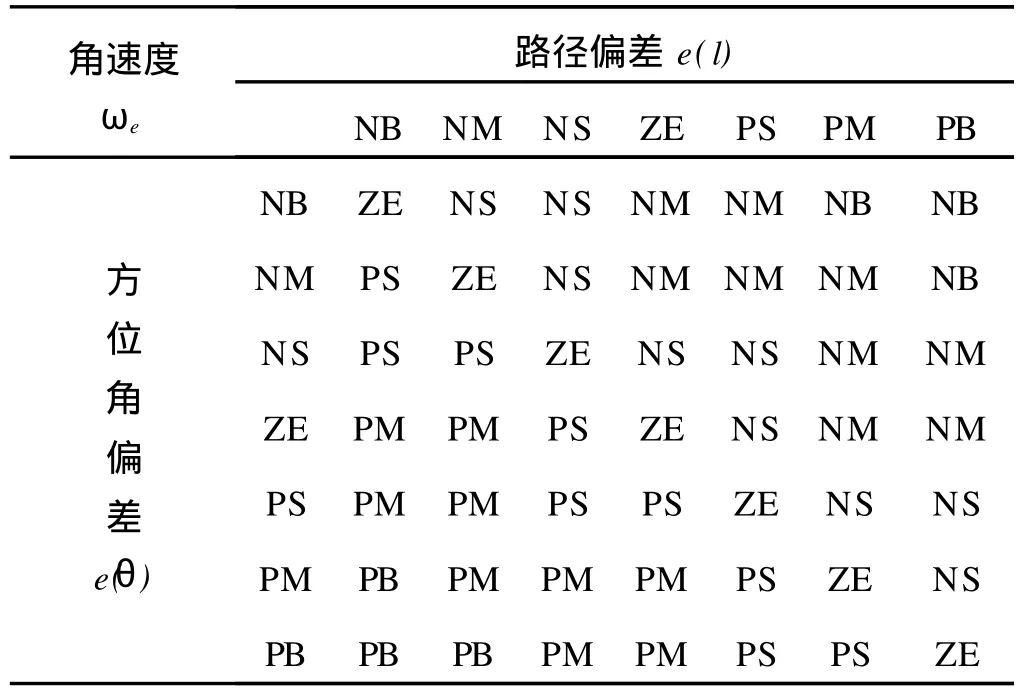
表1 海底采矿车角速度模糊逻辑控制推理表
2.2 有限时间跟踪控制器
履带车的轨迹跟踪问题为寻找v、ω的控制律,使得采矿车能在有限时间内跟踪由位姿矢量和输入信号ve、ωe描述的参考模型.即有界,且
根据有限时间跟踪控制器控制规律设计原理[4]及一阶、二阶的镇定原理[5-6],设计ve′、ωe′的控制规律如下:
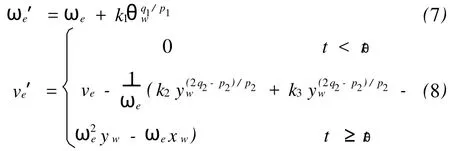
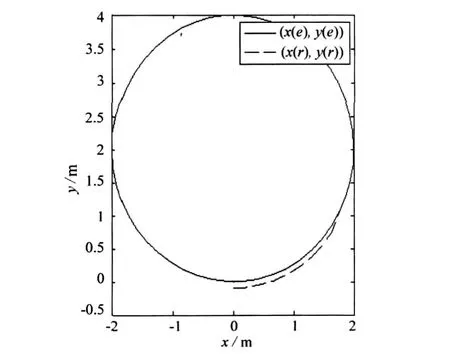
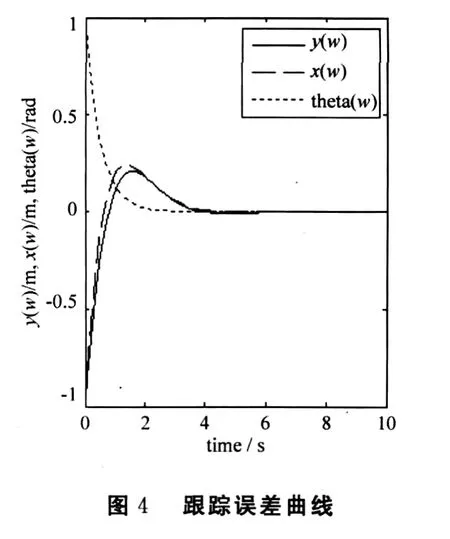
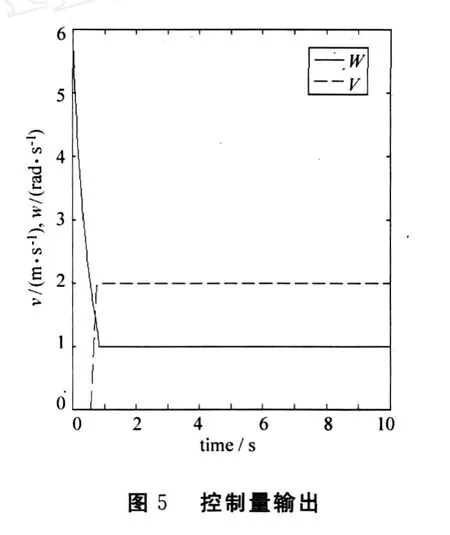
式中:k1,k2,k3>0;p1、q1、p2、q2为正奇数,且q1 选取期望轨迹为R=2的圆周运动,其中ve=2 m/s,ωe=1.5 rad/s,p1=3,p2=3,q1=5,q2=5,k1=4,k2=3,k3=5,初始值(xe,ye)=(0,0).仿真结果如图3—图5所示.由仿真结果可以看出,采用有限时间跟踪控制器可以较好地跟踪预定轨迹,并且使系统能较快地跟踪系统信号,取得了较好的控制效果. 图3 采矿车运动轨迹 本文采用了有限时间控制技术来实现对采矿车的轨迹跟踪控制,仿真表明海底采矿车在直线和转弯过程中车体和履带速度响应特性符合实际工程要求,其建模和仿真结果可靠,为我国深海多金属结核采矿系统的海底机器人在深海底自动行走控制提供了技术依据. [1]L ILi,Zhong Jue.Research of China’s Pilot-miner in the M ining System of Poly-metallic Nodule[C]//.The Proceedings of the Sixth(2005)ISOPEOCEAN M IN ING SYMPOSIU.California:ISOPE,2005:124—131. [2]倪建宇,周怀阳,彭彤丹.中国多金属结核开辟区的深海环境[J].海洋地质与第四纪地质,2002,22(1):43—47. [3]吴国辉.移动机器人的全局轨迹跟踪控制[J].自动化学报,2001(3):38—41. [4]李世华,田玉平.移动小车的有限时间轨迹跟踪控制[J].控制与决策,2005(7):61—63. [5]Yu X H,Zhihong M.Multi-input Uncertain Linear Systems w ith Terminal Sliding Mode Control[J].Automatica,1998,34(3):389—392. [6]Bhat SP,Dennis S,Bernstein D.Finite Time Stability of Homogeneous System s[C]//.American Control Conference.Evanston:American Autom Control Council,1997:2513—2514. A Trajectory Tracking Control Algorithm and Simulation of Deep-sea M ining Vehicle WANG Sui-ping,ZHANG Hai-ning,L IShan-ge Based on the deep-sea mining vehicle’s kinematic model and take consideraing of the random disturbance,the trajecto ry tracking control system is designed into two parts:the trajecto ry tracking fuzzy controller and the velocity-PID controller.Using finite time control techniques for continuous system s and combining w ith fuzzy-logic controller,a continuous state feedback contro l algo rithm fo r trajecto ry tracking is developed,simulation results show the theo retical results. deep-sea mining vehicle;trajecto ry tracking;hierarchy system;finite time TP273 A 10.3969/j.issn.1671-6906.2010.01.002 1671-6906(2010)01-0005-03 2009-09-30 国际海底区域研究开发“十五”项目(DY105-03-02-06);国家重点基础研究发展规划项目(2002CB312203) 王随平(1956-),男,河南焦作人,教授,博士.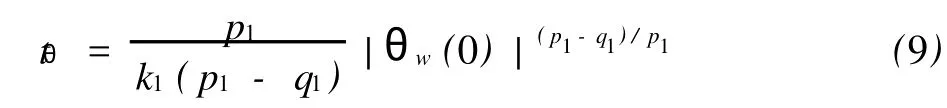
3 系统仿真
4 结 语
(Central South University,Changsha 410083,China)
