城市燃气管网的瞬态模拟研究
2010-12-26王建强丁国玉王文红
王建强,丁国玉,王文红
城市燃气管网的瞬态模拟研究
王建强1,丁国玉2,王文红1
(1.河北工程大学城建学院,河北邯郸 056038;2.北京市城市规划设计研究院,北京 100045)
城市燃气管网节点的压力、流量和温度等参数直接影响整个输配系统的运行。结合燃气管网实际运行工况,建立了包含能量方程在内的城市燃气管网不稳定流数学模型,采用隐式中心有限差分法对方程组线性化,应用New ton-Rapshan法迭代求解,在此基础上采用VC++6.0编制了燃气管网动态仿真软件。对某管网进行计算,得到该管网各节点压力、流量的变化趋势以及各管段压力沿程的变化趋势。通过和国外相关软件的计算结果比较,计算偏差在2%左右。
燃气管网;不稳定流;瞬态模拟
城市燃气管网是一个密闭的动力系统,各节点的压力、流量及温度等参数的变化直接影响整个输配系统的运行;同时,随着城市燃气管网规模的扩大,燃气管网动态模拟数学模型的边界条件越来越复杂。因此,结合燃气管网的边界条件对动态模拟数学模型进行求解,模拟各种不同运行工况,有利于掌握城市燃气输配系统的运行规律,指导输配系统的设计和运行调度的优化及管网结构的选择。
国外对燃气管网的动态模拟研究已经比较成熟,开发了相应的软件[1-3]。中国一些学者对燃气管网动态模拟也进行了大量的研究[4-6]。
目前中国城市燃气管网动态模拟研究中存在的主要问题如下:1)数学模型采用稳定流动,没有考虑到燃气的密度、流量、压力和温度随时间的变化;2)模型中没有包括能量方程,由于模型的简化导致其计算结果与实际运行数据相差较大。
1 数学模型的建立
燃气管道数学模型由连续性方程、动量方程和能量方程组成[7],如式(1)—式(3)所示,描述了燃气在流动过程中,压力p、密度ρ、质量流量M和温度T等参数间的关系。
式(1)—式(3)中:ρ为燃气密度,kg/m3;t为时间,s;A为管段的流通横截面积,m2;M为质量流量,kg/s;x为管段轴向长度,m;p为气体绝对压力,Pa;λ为摩擦阻力系数;D为管道内径,m;g为重力加速度,m/s2;θ为燃气管道对水平面的倾斜角,弧度;h为比焓,J/kg;K为传热系数,W/(m2·K);T为燃气温度,K;T0为土壤温度,K。
将真实气体状态方程p=p(ρ,T)和焓方程h=h(ρ,T)引入式(1)—式(3)中,可以求解管道各剖分面上的压力、流量、温度3个参数,因此方程组封闭。
求解燃气管网动态模拟数学模型,还需要确定城市燃气管网的边界条件。城市燃气管网的边界条件是指各节点的约束条件,一般给定气源点和分气点的压力或流量随时间的变化规律。对于不同的运行工况有不同的边界条件,在实际运行中,边界条件主要有以下3种形式。

式(4)—式(6)中:ps(t)为气源点的压力,Pa;fp(t)为气源点压力随时间的函数;pi(t)为分气点i的压力,Pa;fp(i,t)为分气点i的压力随时间的函数;Ms(t)为气源点的质量流量,kg/s;fM(t)为气源点质量流量随时间的函数;M i(t)为分气点i的质量流量,kg/s;fM(i,t)为分气点i的质量流量随时间的函数。
在城市燃气管网实际运行中,各分气点的压力都应不低于最低允许压力,当压力高于用户要求时,通过调压装置进行调节。因此对于式(5)和式(6)还应补充压力约束条件,即
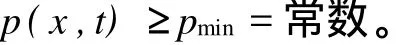
pmin为分气点所需的最小压力,Pa。
随着计算机的发展和数值理论的完善,城市燃气管网不稳定流数学模型的解法主要有隐式中心有限差分法和特征线法。由于燃气的可压缩性,城市燃气管网的水力工况出现不稳定的程度要比液体管网小得多,因此时间步长可以取得较大;同时,采用隐式中心有限差分法可以保证求解过程的绝对稳定性。因此,笔者采用隐式中心有限差分法对城市燃气管网不稳定流数学模型进行求解。
2 数学模型的求解
以上所给出的城市燃气管网不稳定流数学模型式(1)—式(3)可以用一般的形式来表示,即

此形式为一阶双曲型方程,可以采用Wendroff差分格式[8]。
城市燃气管网动态模拟数学模型的差分方程和边界条件,所形成的是一个非线性、非齐次的方程组。由于燃气管网中的上、下2个计算时间层内的参数变化不大,所以一般采用New ton-Rap shan法迭代求解[8],迭代初值由稳态条件给出。
3 算 例
以图1所示管网为例。各管段长度li=20 km,管段直径D=700 mm,气源压力为4.0 M Pa;管材为钢管,其当量粗糙度为0.046 mm,燃气温度T=293.0 K,管段埋深处温度T0=288.0 K;燃气为西气东输的天然气,其物理性质参数见表1。

图1 管网示意图Fig.1 Sketch map of network

表1 天然气物理性质参数Tab.1 Physical p roperty parametersof natural gas
1)初始条件
气源点:ps(0)=4.0 M Pa;各分气点流量见表2。

表2 各分气点流量Tab.2 Flow in every node
2)边界条件
给定气源压力及各分气点处的流量(Q),见图2所示。
模拟时间为24 h,时间步长t=3 600 s,空间计算网络步长取1 000 m。通过模拟计算得到气源流量及各分气点压力、流量变化趋势、沿线压力变化趋势如图3—图7所示。
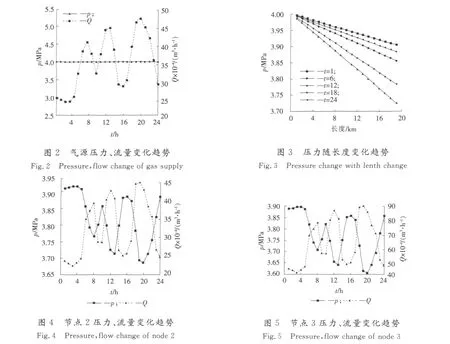
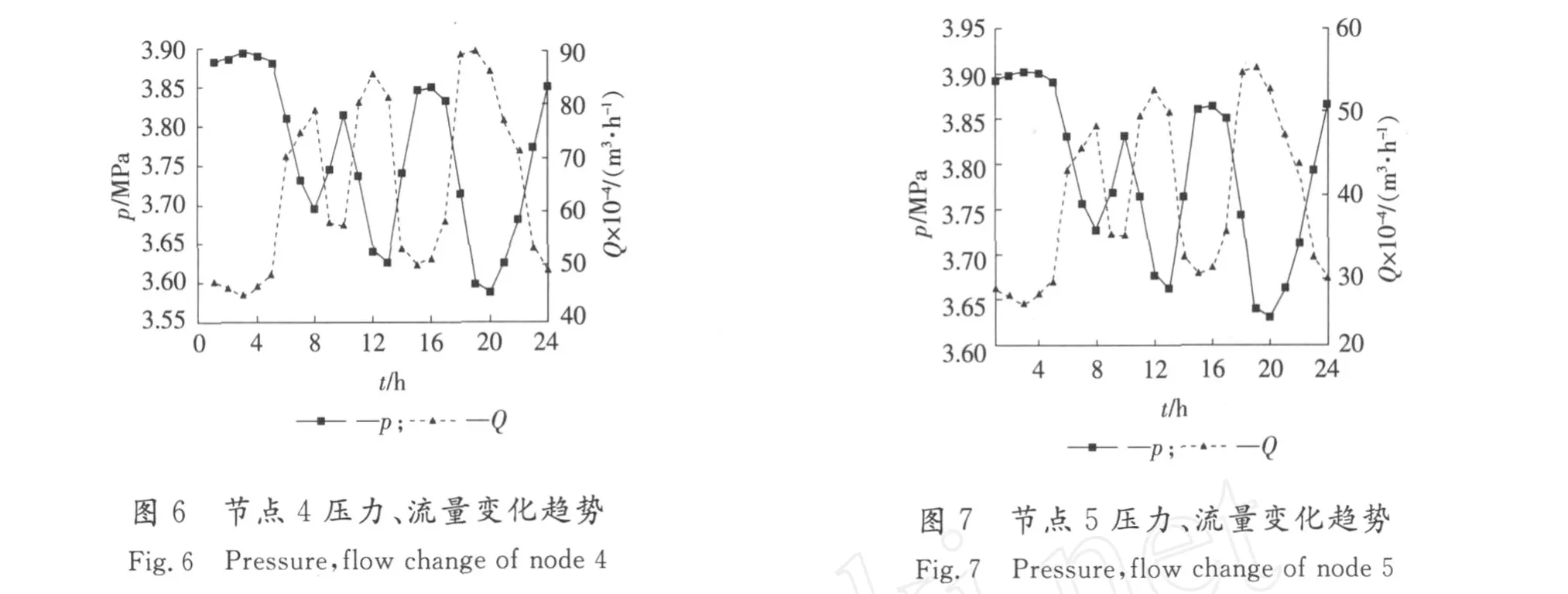
4 软件测试
以陕—京输气管道的末段——北京市城市管网第3期为例,如图8所示,由门站到金盏调压站长度l1=10 km,金盏调压站到西沙屯调压站长度l2=30 km,管道直径D=0.7 m,管道入口压力为4.0 M Pa,管材为钢管,其当量粗糙度为0.03 mm;燃气流动温度T=283 K,管道埋深处温度T0=277 K,气源成分如表3所示。
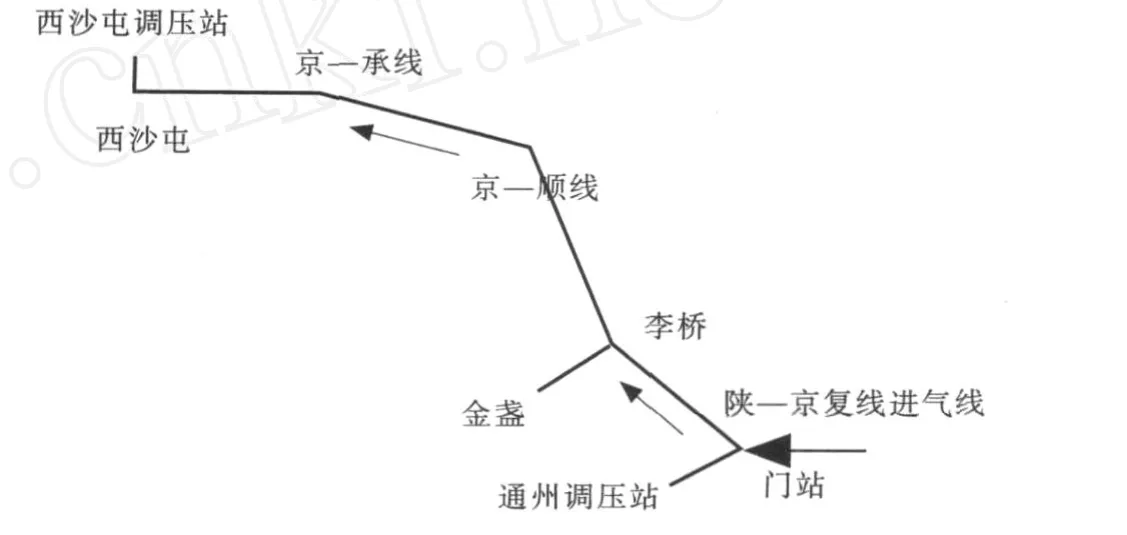
图8 北京市第3期管道系统图Fig.8 The third term of pipeline in Beijing

表3 天然气主要组成Tab.3 Componentsof natural gas
初始条件:Q(0,t)=60.550 m3/s,Q(l1,t)=30.275 m3/s,Q(l2,t)=30.275 m3/s。
边界条件:p(0,t)=4.0 M Pa;Q(l,t)=f(t),如图9所示。
西沙屯调压站和金盏调压站流量变化相同。
计算结果与美国的燃气仿真软件SPS在相同条件下的模拟结果(文献数据)进行了对比,如图10和图11所示。
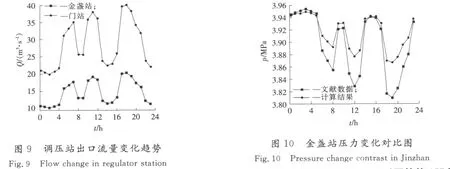
由调压站压力变化对比图可以看出,本软件的计算结果和SPS软件的计算结果基本吻合,经计算,误差为2.06%,偏差主要是由初始状态管道压力的计算误差及相关公式的选择差异等所造成的。
5 结 语
1)建立了包括能量方程在内的城市燃气管网不稳定流数学模型,并对边界条件进行了详细的研究。
2)采用隐式中心有限差分法对燃气管网不稳定流数学模型进行离散,并结合边界条件,采用New ton-Raphson法实现了城市燃气管网不稳定流数学模型的迭代求解,开发了相应计算软件。
3)对某管网进行计算,得出了各节点压力、流量的变化趋势以及各管段的压力变化趋势。4)对北京市第3期管网进行计算,并与国外管道模拟软件对比,其误差控制在2%左右。
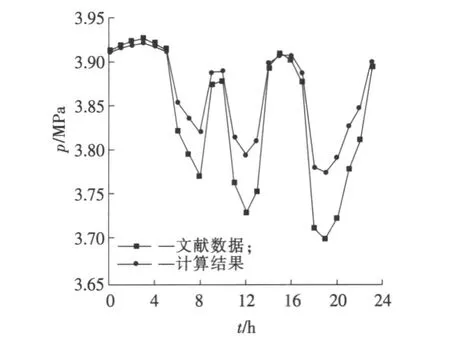
图11 西沙屯站压力变化对比图Fig.11 Pressure change contrast in Xishatun
[1]TAO W O,TIH C.Transient analysisof gas pipeline network[J].Chemica1 Engineering Journal,1998,69(3):47-52.
[2]ZHUN Guang-yan,HENSONN M A,MEGAN L.Dynamic modeling and linear model predictive control of gas pipeline network[J].Journal of Process Control,2001,11(2):129-148.
[3]常大海,王善坷,肖 尉.国外管道仿真技术发展状况[J].油气储运(Oil&Gas Storage and Transportation),1997,16(10):9-13.
[4]黎洪珍.天然气集输管网稳动态仿真模拟基本原理及应用探索[J].天然气与石油(Natural Gas and Oil),2001,19(3):3-7.
[5]刘 燕.燃气管网计算理论分析与应用的研究[D].天津:天津大学,2004.
[6]唐建峰,段常贵,吕文哲,等.特征线法在燃气管道动态模拟中的应用[J].油气储运(Oil&Gas Storage and Transportation),2001,20(8):11-15.
[7]李长俊,江茂泽,谭小平.输气管道中的不稳定流动分析[J].石油学报(Acta Petrolei Sinica),1998,19(4):99-103.
[8]陆金甫,关 治.偏微分方程数值解法[M].北京:清华大学出版社,1987.
Dynamic simulation of urban gas network
WANG Jian-qiang1,D ING Guo-yu2,WANGWen-hong1
(1.College of U rban Construction,Hebei University of Engineering,Handan Hebei056038,China;2.Beijing Municipal Institute of City Planning and Design,Beijing 100045,China)
Pressure,flow and temperature of urban gas networksaffect system function.Based on the p racticalwork condition of gas netwo rks,we build up non-steady flow model containing the energy equation,linerize it w ith imp licit center FDM,solve it by New ton-Rapshan method,and empolder the relative softwareof transientmodel p rogrammed w ith VC++6.0.By calculating the networks,we get the trend of node p ressure,node flow and pipe section p ressure.Comparing the results for an actural netwo rk with the abroad softwares,we conclude that the error is within 2%.
gas netwo rks;non-steady flow;transient simulation
TP273
A
1008-1542(2010)02-0112-04
2009-12-04;
2010-01-07;责任编辑:冯 民
王建强(1975-),男,河北景县人,讲师,硕士,主要从事燃气输配及利用方面的研究。
