基于SVM的核电装备制造业供应风险预测模型研究
2010-12-23石春生孟大鹏哈尔滨工业大学哈尔滨150001
□石春生 孟大鹏 [哈尔滨工业大学 哈尔滨 150001]
基于SVM的核电装备制造业供应风险预测模型研究
□石春生 孟大鹏 [哈尔滨工业大学 哈尔滨 150001]
基于对核电装备制造业供应风险的因素识别,确立风险预测指标体系;对国内某家重点核电装备制造企业及其60家供应商进行问卷调研及深度访谈,运用支持向量机及libsvm技术建立供应风险的预测模型;最后的案例研究表明了该预测体系的可行性与可靠性。
支持向量机; 核电装备; 供应风险; 预测模型
基于大力推进核电工业的战略规划,AP1000进程中的中国核电事业面临两大难题:一是加速实现核电技术的自主化,建立独立、完备、有中国特色的核电工业体系;二是如何有效地应对自主化进程中关键部件及物资过度依赖于进口引发的供应风险。目前我国尚未实现全部装备的设计、制造自主化,有20%的关键装备尚依赖于进口,由此产生的供应质量及交货延迟问题已成为核电工业发展的瓶颈。为化解供应风险、保证物资供应,技术、制造领域的理论及实践者已纷纷投入精力并取得了相应成绩;而从管理角度对供应风险进行分析、预测研究的课题尚未引起关注,现有研究多是概念、策略性的一般表述,其科学性和指导意义有待考证。为突破这一局限,本文从供应商及风险管理理论出发,在风险识别的基础上利用支持向量机的方法建立风险预测模型,以期为风险控制提供客观依据。
一、支持向量回归理论
支持向量回归机(Support Vector Regression,SVR)是在支持向量机(Support Vector Machine,SVM)分类模型的基础上引入一个用于距离修正的ε作为损失函数,以确保对偶变量的稀疏性和全局最小解的存在和可靠泛化界的优化。
(一)不敏感损失函数ε
基于结构风险最小化原则,构建针对实函数集的SVR模型,需引入ε建立损失函数:

(二)支持向量回归机
将SVR表述为:给定训练样本集(xi,yi) ,x∈R,i=1,..n,引入ε作为风险函数

引入Lagrange系数:

求解最优问题及iα和*iα后,可以求得回归方程:

二、基于SVM的供应风险预测模型构建
(一)指标体系的确立
1.相关理论假设
外部环境风险:由外部环境诱发的供应风险,如:自然灾害对厂址、物流的摧毁;经济政策、金融风暴引发的供应危机;技术革新对现有技术的冲击及鉴于核工业的敏感性,受到不同国家政治体制作用而引发的供应风险。建立假设:
H1:自然环境因素与供应风险相关
H2:政治环境因素与供应风险相关
H3:经济环境因素与供应风险相关
H4:科技环境因素与供应风险相关
内部合作风险:由供求双方企业能力与合作意愿交互作用而引发的供应风险。
(1)供应商的企业能力:
技术:Burns[1]和George Stalk[2]指出,企业的技术能力包括技术引进、扩散及创新能力。Amos指出,技术能力是学习、培训及科研共同作用的结果,以R&D人才培养、R&D经费投入为关键。鉴于技术自主化对于核电装备制造业供应风险防范的重要意义,建立假设:
H5:供应商的R&D人员比例与供应风险相关
H6:供应商的R&D投入强度与供应风险相关
H7:供应商的新产品产值比例与供应风险相关
质量:Dickson的经典研究表明,质量是企业最重要的能力。Berrittella[3]将质量保证能力列入企业考核的重点。陈实将服务指标列入供应商评价体系中。Tobias[4]认为,对供应商评价不仅要考虑质量、技术,还应考虑柔性、服务及多样性指绩效。建立假设:
H8:供应商的质量管理状况与核电装备制造业的供应风险相关
H9:供应商的服务及时率与核电装备制造业的供应风险相关
(2)核电装备制造企业的能力:
管理:Dale[5]指出,能力的评价体系应涵盖管理的有效性。Tobias[6]认为,与管理相关的协作能力将影响双方合作。马士华教授强调物资管理的失败会带来供应风险。鉴于核电装备物资单价高、付款额度大,将付款及时率指标列入企业能力的评价范畴。建立假设:
H10:采购商的关系管理能力与供应风险相关
H11:采购商的准期付款率与供应风险相关
控制:Hallikas[6]指出,质量、进度等来自于供应商的行为是供应风险的诱因。Uzzi[7]将战略、运作及双方对过程的控制归为供应风险的诱因。建立假设:
H12:采购商的质量控制能力与供应风险相关
H13:采购商的进度控制能力与供应风险相关
支持:Patton[8]提出,采购商的支持有利于供应商能力的提升;Zsidisin[9]指出,人才缺乏将诱发供应风险。现有供应商大都存在技术能力、专业人才缺乏的情况,建立假设:
H14:采购商的技术支持情况与供应风险相关
H15:采购商的人才支持情况与供应风险相关
(3)双方的合作意愿:Steele认为供应风险的诱发源于供应与需求不平衡。Wendy[10]提出,除了考虑成本、质量以外,管理相容性等意愿指标也需引起双方关注。鉴于核电装备制造业物资供求市场上经常出现供求不平衡以及由此引发合作依赖偏差的状况,建立假设:
H16:周期供应额与供应商的全部供应额的比例与供应风险相关
H17:周期采购额占采购商的全部采购额的比例与供应风险相关
H18:合作物资的市场需求厂家数量与供应风险相关
H19:合作物资的市场供应厂家数量与供应风险相关
H20:合作物资的市场供需状况与供应风险相关
H21:供应商是否具备核级资质与供应风险相关
2.实证研究
利用研究变量之间密切程度的相关分析实证前文假设的科学性。考虑到数据的特点,采用基于秩次大小、对变量分布不作要求的Spearman方法计算相关系数:

上式中:d为每对变量(X,Y)的秩次之差,n为对子数。
借助SPSS12.0,经由Analysis->Correlate->Bivariate>Spearman操作,相关分析的结果如表1所示:是否核级,人才、技术支持,自然、经济、科技环境指标未通过显著性检验,表示这6个指标与供应风险的相关性不明显,假设未得到验证;除此之外的15个假设得到了验证,对应的15个指标构建了供应风险的影响因素并用于风险预测的研究。
(二)实现技术及数据处理
1.实现技术:应用在国际著名的研究机构中享有很高的威望的Libsvm软件包作为SVM预测模型的实现技术,操作平台为Windows2000。
2.数据处理:为防止数据库中特征值极大的指标对特征值极小的指标产生控制效应,避免计算过程中数据过大的问题,应Libsvm的要求,调用命令E:LibSVMwindowsSvmScale –s data0.range data0.scale >data.scale,对60个样本数据进行归一化处理。
(三)试验步骤
步骤1:模型的训练
1.参数寻优:通过Libsvm的自动交互检验功能寻求最优参数,力求系统的MSE最小。
输入:E:python26>python e:python 26gridreg ression.py-svmtrain e:LibSVMwindows svmtrain.exe–gnuplot e:gnuplot binpgnupolt.exe –log2c-10,10,1 –log2g -10,10,1 –log2p -10,10,1 -v 10 –s 3 –t 2 e:LibSVMwindows finaltrain.txt>gridegression final train.parameter
-log2c,-log2g,-log2p:设置参数c,g,p的范围和步长分别为[-10,10],1;
输出:整理finaltrain.parameter获得MSE的最小值及对应的最优参数c,g,p。

表1 相关分析结果
2.训练并获得SVR模型:基于最优参数进行回归模型的训练,以获取SVR模型。
输入:C:LibSVMsvmtrain –s 3 –t 2 –c –g –p
输出:整理finaltrain.model获得SVR模型,包括二次规划最小值及判决函数常数项。
3.求解回归方程:总结模型的各项输出,求解未知项,获得回归方程的表达式。
根据输出项g,确定BFR的表达式;提取αi−αi*值,确定回归方程。
步骤2:模型的预测
输入:C:LibSVMwindows>svmpredict finaltest.txt finaltrain.txt.model out.txt
输出:整理输出文件out.txt,获得经SVR预测后finaltest.txt对应的预测结果。
步骤3:模型的评价
机器学习及统计理论用于模型评价的系数主要有MSE,MD,CD和CRM。令xi与分别表示第i家供应商供应风险的实际值与回归模型求得的预测值。
(1)均方误差MSE(Mean square error):实际值与预测值之差平方的期望,其值越小,表示模型预测的误差越小:

(2)平均差MD(Mean difference between measurement and simulation):实际值与预测值之差的平均数,反映模型的一致性。MD>0,表示预测值相对于实际值偏低;MD<0,则预测值相对于实际值偏高;MD=0,模型的模拟效果最好:

MD的t检验值(t检验所用自由度为n−2),若成立,则模型系统误差不显著,模拟效果较好;反之,模型系统误差较显著,模拟效果较差。
其中:

(3)确定系数CD(Coefficient of determination):实际值与预测值变异度的比值,反映二者变异的一致性。CD=1,表示二者变异相同;0<CD<1,模型存在一定的系统误差;CD>1,则模型不能完全描述个别极值:

(4)整群剩余系数CRM(Coefficient of residual mass):全部预测值之和偏离全部实际值之和的程度。CRM<0,表示整体预测值大于实际值;CRM>0,则整体预测值小于实际值;其值越接近于0,系统误差的可能性越小,模型的一致性越好:

三、算例
(一)数据来源及处理
对我国某家重点核电装备制造企业及其供应商进行调研。调查形式的设计及内容的权衡,来自于综述理论成果和研究者自身学习与工作经验的总结。结合企业访谈和调查问卷的方式,从定性、定量角度共同建立数据库:发放问卷180份,回收有效问卷120份,其中,60份来自于核电装备制造企业,60份来自于供应商。经Libsvm命令归一化处理后,为实现交叉对比,将60个样本随机生成两组:第一组由40个样本训练模型,对其余20个样本进行风险预测;第二组由20个样本训练模型,对其余40个样本进行风险预测。
(二)模型的训练
两组模型训练输出如图2及图3所示。整理finaltrain.paramete得出两组最优参数分别为:c=1240,g= 0.00195,p= 0.0039;c=4,g= 0.0078,p= 0.00383。
确定两组BFR的表达式为:
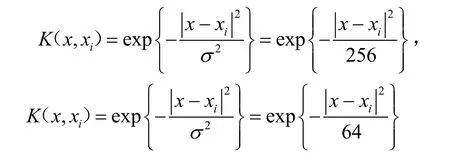
2.两组回归方程:整理输出finaltrain.model提取两组αi−αi*,结合BRF求


图1 第一组SVR模型

图2 第二组SVR模型
(三)模型的预测
整理输出out.txt,比较实际值与预测值,生成表2和表3。
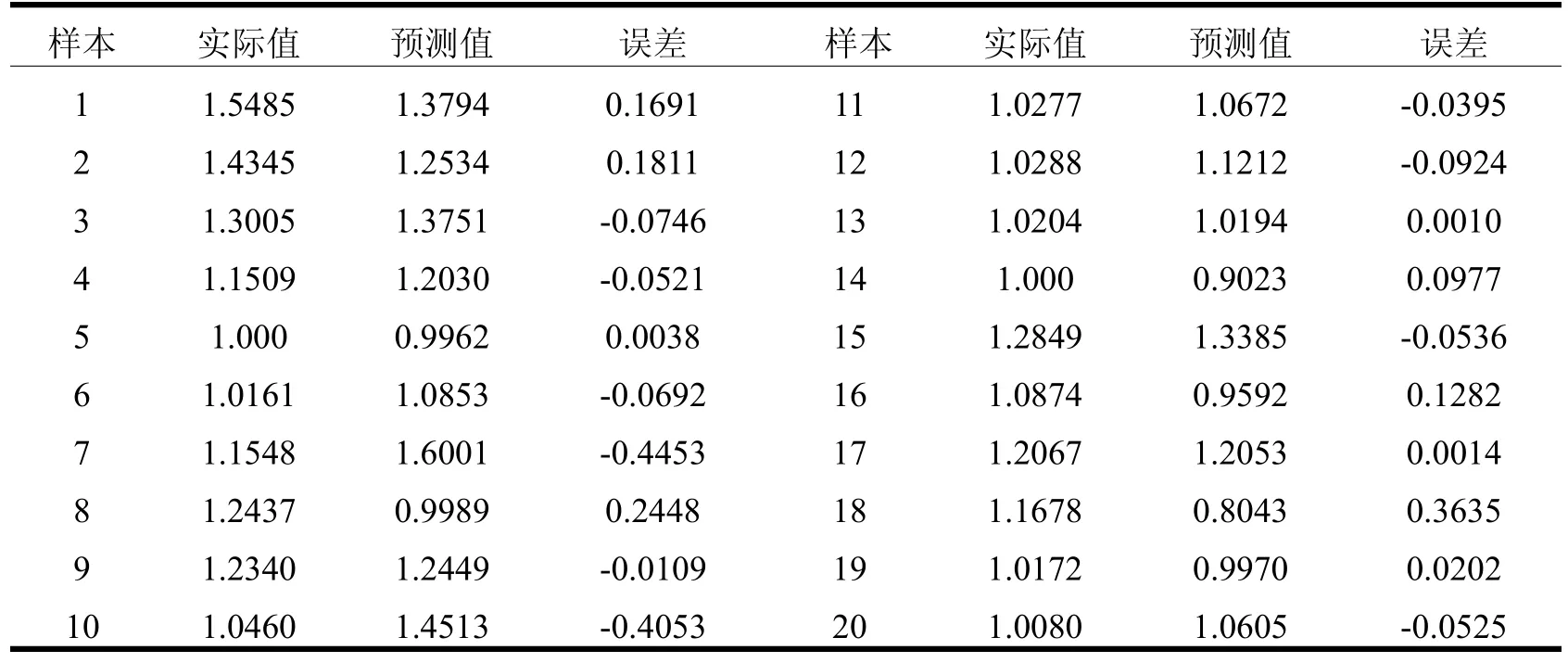
表2 第一组SVR模型预测值与实际值的比较

表3 第二组SVR模型预测值与实际值的比较
(四)模型的评价
分别求得预测模型的评价系数MSE,MD,CD和CRM,如表4所示。

表4 两组SVR模型的系数比较
如表4所示:第一组SVR模型MSE为0.0336,小于第二组,则其误差小于第二组。第一组SVR模型MD= −0.0042 <0,预测值偏高于实际值;第二组MD=0.0471>0,预测值偏低于实际值;第一组MD比第二组更趋近于0,预测偏差小于第二组;两组MD的t检验值皆小于t0.05,系统误差不显著。第一组SVR模型CD=0.5907<1,模型存在一定系统误差,但可描述全部指标特征;第二组SVR模型CD=4.3748 >1,模型系统误差较小,但可能无法描述个别极端值;第一组模型的CD更趋近于1,系统拟和度优于第二组。第一组SVR模型的CRM=-0.0037 <0,预测值偏高于实际值;第二组SVR模型的CRM=0.0388 >0,预测值偏低于实际值。第一组CRM比第二组更趋近于0,其预测偏差较小。综合而言,两组预测模型的系统误差及精度都在可接受的范围内;第一组SVR模型略优于第二组SVR模型。
四、结束语
在对核电装备制造业供应风险因素识别的基础上,运用支持向量回归机及Libsvm的技术构建了供应风险预测模型。由于支持向量机的目标是在现有资源下寻求最优解,样本数据量较小的情势下亦能收到理想的预测结论,使得该模型具有较好的推广性。本研究期望成为核电装备制造企业在应对供应风险过程中,对供应商进行事前及事中考评、测量供应风险度的有效方法论。
[1]BURNS, STALKER. The Organization of Innovation[J]. Knowledge Management and Organisational Design, 1996,(1):77-92
[2]STALK G, EVANS P. Competing on Capabilities, The New Rule of Corporate Strategy [J]. Harvard Business Review,2002, (3):12-15.
[3]BERRITTELLA. An Analytic Hierarchy Process for the Evaluation of Transport Policies to Reduce Climate Change Impacts [J]. Fondazione Eni Enrico Mattei, 2007, (1):4-8
[4]SCHOENHERR T, TOMMALA V M R, HARRISON T P. Assessing supply chain risks with the analytic hierarchy process: Providing decision support for the offshoring decision by a US manufacturing company [J]. Purchase and Supply management, 2008, (14): 100-111.
[5]DALE, SHAW P. Statistical process control: An examination of some common queries [J]. International Journal of Production Economics, 2001, (22): 33-41.
[6]HALLIKAS, KUMAR K. Sutainable collaboration,Managing conflict and cooperation in interrogational systems[J].Mis-quarterly, 2006, (20): 279-300.
[7]UZZI B. Social structure and competition in inter firm networks: The paradox of embeddedness[J]. Administrative Science Quaterly, 1997, (42): 35-67.
[8]PATTON, YATES J, RENJAMIN R K. Electronic markets and electronic hierarchies [J]. Communication of the ACM, 1987, (30): 484-497.
[9]ZSIDISIN. Competition for competence and interpartner learning within international strategic alliances [J].Strategic Management Journal, 1991, (12): 83-103.
[10]WENDY, ROBERT G, KEVIN J M. Relational Contracts and the Theory of the Firm [J]. Quaterly Journal of Economics, 2002, (117): 39-48.
Research on the Supply Risk Prediction Model of Nuclear Power Equipment Manufacturing Industry Based on SVM
SHI Chun-sheng MENG Da-peng
(Harbin Institute of Technology Harbin 150001 China)
Based on the factor identification of nuclear equipment manufacturing industry, prediction index for supply risk is established. To make investigation on a famous nuclear power equipment manufacturing enterprise and the 60 suppliers, the method of support vector machine and libsvm software are used to establish supply risk prediction model. Final case study demonstrates the feasibility and reliability of model.
support vector machine; nuclear power equipment; supply risk; prediction model
F253.9
A
1008-8105(2010)05-0023-06
2010 − 05 − 12
国家自然科学基金项目(70972096)
石春生(1958 − )男,哈尔滨工业大学管理学院教授,博士生导师;孟大鹏(1981 − )女,哈尔滨工业大学管理学院博士研究生.
编辑 何婧
