OLED器件寿命衰退模型的MATLAB分析计算
2010-12-21王忆锋唐利斌
王忆锋,唐利斌,岳 清
(昆明物理研究所, 昆明650223)
有机发光二极管(Organic Light Emitting Diode,OLED)是由光刻电极基板与有机发光材料构成的显示器件,长寿命、高亮度、低功耗是OLED器件的发展方向[1-2]。驱动电压的变化规律在某种程度上是OLED寿命衰退机制的反映。一般而言,驱动电压随着点亮时间的延长而增加,亮度(或电发光效率)随时间而降低[3]。在实际测试过程中,即使电流密度恒定,驱动电压也会发生变化。本文从计算的角度,介绍了OLED器件寿命衰退模型的MATLAB分析方法。
1 OLED驱动电压与离子浓度的关系
通常的OLED器件寿命测试是在一定电流密度下检测器件亮度随点亮时间的变化关系,然后外推到器件亮度衰减至起始亮度的一半时进行评估的。一般认为OLED器件的偏置电压引入一个与外部电场方向相反的内部极化电场,使得驱动电压随着点亮时间的延长而增加。引起内部极化电场的机制有若干种,其中之一是运动离子在外加偏置电压下的重新分布[3]。
OLED中瞬态运动离子的分布及其与驱动电压的关系可由下列方程描述[3]
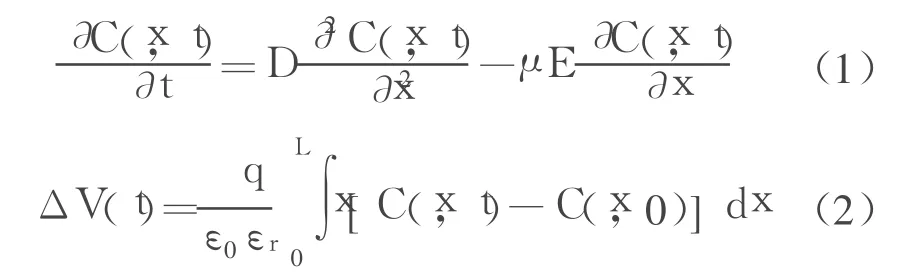
式中, C(x, t)为运动离子浓度;D为扩散系数, μ为迁移率, E为电场强度;ΔV(t)为驱动电压的变化量, q为电子电荷量, ε0为真空介电常数, εr为相对介电常数;L为OLED阴极与阳极之间的距离。
式(1)是一个线性偏微分方程,其初始条件为

另外

其中

粒子数守恒要求

根据上述条件,利用MATLAB提供的laplace()命令对式(1)做拉普拉斯变换,有

式(7)是一个常微分方程,调用MATLAB的dsolve()命令,可以求出

如果能求出上式的拉普拉斯逆变换,那么即可得到C(x, t)。但是利用MATLAB提供的拉普拉斯逆变换命令ilaplace(),无法求解式(8)。
如果引入变量

则式(8)可以化为

虽然可以用 ilaplace()命令求出式(10)对应的C(x, T),但是要实现从C(x, T)→C(x, t)的转换并不容易。事实上,利用数学物理方程理论中介绍的常见方法均无法求出该模型的解析解。
2 模型的近似求解
满足式(3)和(4)的函数C(x, t)应该具有下列形式

其中待定函数f(ξt)要满足条件f(0)=1, f(∞)=0。若干这样的函数形态可以列出如下

式中, erf()为误差函数,定义为

erfc()为余误差函数,定义为

MATLAB中有erf()和erfc()命令可供直接调用。另外,由于负指数函数可以用有理函数近似[4],所以实际上f(ξt)最终可归为负指数函数和误差函数两种形式。
因为ξ与t之乘积应是一个无量纲的数值,故关于ξ的选取应考虑两个因素,首先其量纲应为1/s;其次为了引入空间位置变化的影响, ξ中应包含坐标变量x。
扩散率D的量纲为cm2/s, 电场 E的量纲为V/cm,迁移率μ的量纲为cm2/V◦s;故对于指数函数可以取

而对于误差函数erf(),可以取

3 模型计算与参数拟合
将式(11)代回式(2),可以写出

其中

注意到在MATLAB中当f(ξt)为误差函数时,I1和I2两项积分不易做符号计算,故本文中选用负指数函数,即取式(15),这时可以利用MATLAB的int()命令计算出式(19)所示的三个定积分的值,进一步整理后可得,

其中

另外,类似于在PN结IV特性曲线中的引入理想因子的做法[4-5],在式(20)中引入三个参数α、β和γ,即

以此来描述实际测试数据与理论模型之间的偏离程度。已知测试数据后, 这三个参数容易通过调用MATLAB的最小二乘曲线拟合命令lsqcurvefit()求出[6]。
若假设OLED器件内的电场为常量,则电场E与施加的偏置电压V及长度L之间有如下关系

将式(24)代入式(23),可以得到ΔV(t)与不同偏压之间的关系。
4 恒流离子源条件下模型的有限差分矩阵计算
在实际使用过程中, OLED电极材料中的离子可能会发生迁移,形成一个恒流离子源,与这种情况对应的条件是

另设初始条件仍为式(3)。在这两个条件下,利用数学物理方法理论中介绍的各种技巧,很难求解式(1);用试凑法也不易找到同时满足这两个条件的解析表达式。下面介绍基于有限差分的数值算法。
如图1所示,在x轴方向以Δx为间距,将求解区域等间距划分为M个区域,计有(M+1)个节点,其中边界节点2个。设n为时间坐标,将时间坐标上的计算区域划分为T个等份,共有(T+1)时间节点,两个时间节点之间的间隔Δt称为时间步长。引入时间量后的节点坐标记为Ψ(mΔx, nΔt),省略各步长项后可写为Ψ(m, n),或者进一步简记为Ψ(n)(m)。

图1 顺序排列的等间距网格节点
差分法的基本思想是在各网格节点对函数做泰勒级数展开并取近似,用差商代替导数,将偏微分方程转化为一个线性方程组形式的差分方程,通过求解线性方程组得到微分方程的近似解。差分有不同的格式。设已知(m, n)的值。在(m, n+1)处,时间导数用向后差分近似,空间导数用中心差分近似,可得古典隐格式的差分格式。古典隐格式是绝对稳定的[7]。
具体到这里的离子浓度函数C(x, t),在(m,n+1)处,其对坐标x的偏导数可以用(n+1)时刻的中心差分近似为

C(x, t)对时间坐标t的一阶偏导数可以用(n+1)时刻的向后差分近似为

将式(26)~(28)代入式(1),可以得到古典隐格式的差分方程

其中

对整个OLED器件结构离散化,即从m=2 开始直到m=M +1,逐点写出式(29);当进行到最后一个节点时,会出现标号为(M +2)的节点,这时后退一格。整理后可得下列形式的矩阵方程


式中,Γ是一个M×M阶的三对角线矩阵,定义为在MATLAB中可用spdiags()命令生成Γ矩阵[8]。

C(n+1)和C(n)均为M×1阶矩阵,分别定义如下C(n)为初始值或前一时刻离子浓度值及恒流离子源的数值构成的已知量, 其中对式(25)取向前差分,即

C(n+1)为待求未知量,构造出Γ矩阵和C(n)矩阵后, 利用 MATLAB的矩阵左除命令即可求出C(n+1)的值;因为计算得到的C(n+1)本身为离散值,这时利用MATLAB的样条插值积分命令如fnint()等[6,9],即可 计 算出(n+1)时 刻 的ΔV(t)值, 即式(2);再将C(n+1)作为已知量代入第n+2 个时间步长计算C(n+2)的值,如此循环往复直至达到所设定的时间步长时为止。最后利用MATLAB提供的多项式拟合命令polyfit(),对各时刻得到的ΔV(t)值做拟合,可以获得驱动电压的变化量ΔV与时间t之间的多项式函数表达式。
5 结束语
影响OLED器件寿命的主要因素有材料的物理化学稳定性、器件结构的合理性、密封膜层的有效性、有害离子的迁移性等,多数情况下这些因素相互影响和制约,使得对于器件性能衰退机制的全面理解错综复杂。 OLED器件寿命衰退机制的探讨可以粗略地分为两条路径,一条是实验研究与分析,另一条是模型的理论计算与仿真。本文介绍的方法具有一定的普适性,可以有效地解决OLED衰退模型的计算问题;通过拟合,还可以进一步建立模型与测试数据之间的对应关系,从而将理论模型与工艺或实验有机地联系起来。
[ 1] 袁永波,连加容,周翔.空穴阻挡层对有机发光二极管寿命的影响[ J] .电子器件, 2008, 31(1):25-28.
[ 2] 李大勇, 刘明.采用 Al2O3/ITO阳极的有机电致发光器件[ J] .电子器件, 2008, 31(1):22-24.
[ 3] Shen J, Wang D, Langlois E, et al.Degradation Mechanisms in Organic Light Em itting Diodes[ J].Synthetic Metals, 2000,(111/112):233-236.
[ 4] 王忆锋,毛京湘.根据IV曲线形态定性判断PN结性能的一种简易方法[ J] .红外, 2008, 29(4):20-23.
[ 5] Robert F Pierret著.黄如,王漪,等译.半导体器件基础[ M].北京:电子工业出版社, 2004年11月.
[ 6] 薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[ M] .北京:清华大学出版社, 2004年8月.
[ 7] 陆君安,尚涛,谢进,等.偏微分方程的MATLAB解法[ M] .武汉:武汉大学出版社, 2001年8月.
[ 8] 王忆锋,唐利斌.利用有限差分和MATLAB矩阵运算直接求解二维泊松方程[ J].红外技术, 2010, 32(4):213-216.
[ 9] 王忆锋,毛京湘.用MATLAB和样条函数拟合红外探测器相对光谱响应曲线[ J].光电技术应用, 2008, 23(2):46-49.
