杂草算法收敛性分析及其在工程中的应用
2010-12-20陈丹丹秦仙蓉
张 氢,陈丹丹,秦仙蓉,高 倩
(同济大学机械工程学院, 上海201804)
进化类算法是根据自然界中生物的繁衍、进化机制演化而来的一种搜索寻优技术, 它遵循达尔文的“物竞天择,适者生存” 原则, 对一个随机生成的初始种群进行不断迭代进化, 逐步提高种群体的质量,从而逐步逼近所求问题的最优解[1].其中遗传算法(GA)通过随机的选择、交叉和变异算子来完成整个寻优过程,其本质是对上代群体进行随机、无指导性的搜索, 由此导致算法的早熟、局部搜索能力差, 以及中后期搜索效率低.另外, 由于遗传算法的鲁棒性差, 初始参数的设置对结果的影响较大[2].
粒子群算法(PSO)通过群体中粒子之间的合作与竞争产生的群体智能指导优化搜索.在每次迭代时, 根据更新规则改变粒子的位置和速度,通过跟踪微粒自身的历史最优值和群体内所有个体找到的最优值迭代寻找潜在解, 最后通过群体的协作找到最优解.PSO 仍然存在着早熟和收敛放慢的现象,种群的多样性随着迭代增加而下降,导致无法收敛到全局最优解的缺点[3].
蚁群算法(ACO)则模仿蚂蚁觅食机理, 通过状态转移准则依概率搜索前进路径,以信息素强度的局部和全局更新来控制和优化搜索方向.ACO 具有较好的协作性和鲁棒性,寻优特性好, 但存在搜索时间长、收敛速度慢、容易陷于局部最优解等缺点, 其收敛效果和计算效率与参数设置、信息素增量的选取等都有很大关系[4].
2006 年,Mehrabian 和Lucas 提出一种从自然界杂草进化原理演化而来的随机搜索算法——扩张性杂草进化算法(IWO)[5].IWO 充分利用种群中的优秀个体来指导群体的进化, 进化过程中子代个体以正态分布的方式叠加于父代个体周围, 而此正态分布的标准差又随着进化代数而动态地调整变化,兼顾了选择力度和种群的多样性,能够有效克服不成熟收敛,而且算法结构简单、参数少、鲁棒性较好.但原文并未对算法的收敛性进行分析.本文系统分析了IWO 的收敛性, 并将其应用于工程实际优化问题.
1 IWO 算法
有别于一般进化算法, IWO 算法建立了一种子代繁衍机制:按照种群中个体的适应度值按比例分配其所产生子代的数目, 适应度高的个体繁衍的子代数目多, 而适应性较差的个体也有生存和繁殖的机会, 这种机制在加强较优个体周围的局部搜索的同时,兼顾群体多样性,与自然界杂草群落真实发生的状况更为相似[5].
IWO 算法的实现可以通过以下初始化、繁殖、空间分布及竞争淘汰等4 个步骤来完成:
步骤1,参数初始化.
步骤2,在搜索空间内按均匀分布的方式产生N0个初始解.
步骤3 ,更新进化代数及种群中子代个体正态分布的标准差.
步骤4 ,繁殖子代,并将新种群分布于搜索空间.按适应度值大小分配个体产生的子代个体数目, 适应度值最大的个体产生的子代数目最多, 适应度值最小(fmin)的个体产生的子代数目最少,其余各个个体生成的子代个体数目与其适应度值服从线性关系.以父代个体为均值,子代个体以正态分布方式分布于父代个体周围,产生的子代个体作为新种群.判断新种群个体数目是否达到最大种群规模pmax,若小于pmax,转步骤3 ,再转步骤4 ;否则转步骤3 再转步骤5 .
步骤5 ,竞争淘汰,适者生存.当种群数目达到或超过pmax时,按步骤4 的相同方式进行种群繁殖和子代个体分布, 然后父代个体与子代个体按适应度值大小一起进行排列, 消灭其中适应度值较低的个体, 保持群体规模为pmax .
步骤6 ,判断是否达到最大迭代代数Tmax,若当前进化代数小于Tmax,重复步骤3 及步骤5 ;如果达到了Tmax,则种群中适应度最好的个体作为最优解输出.
2 IWO 算法的收敛性分析
2.1 IWO 算法全局收敛的基础
对于一种算法, 其收敛性往往是人们所关心的首要问题.IWO 算法在进化过程中依赖优秀个体的指导信息进行繁殖进化的机制是算法收敛的基础,算法中子代个体分布的标准差的动态调整是算法收敛的关键, 以正态分布的方式将子代个体叠加于父代个体周围, 使算法能够兼顾选择力度和群体多样性, 有效避开局部极值点,为算法的全局收敛提供了稳定的保障.而且,算法中各参数的取值范围较为宽裕, 对初始种群的依赖性也不高.
IWO 算法避开局部极值, 有效实现全局寻优的因素主要有以下几点:
(1)IWO 算法在初始化种群时, 以均匀分布的方式随机将初始种群分布于整个搜索空间内, 保证了初始种群的多样性.
(2)在进化过程中, 一旦发现一个优秀的个体(即适应度高的可行解),类似的个体亦将大量繁殖.优秀个体不是被机械地保留和利用, 而是通过加强在其周围的局部搜索, 充分发掘利用优秀个体所反映的特征信息,变盲目产生子代个体为有指导地产生子代个体, 通过群体中优秀个体的进化来指导整个群体向最优解进化.
(3)子代个体以正态分布的方式, 叠加在父代个体周围.由正态分布的知识可知,子代个体的产生多集中于上一代优秀个体的附近,但也顾及了上一代优秀个体附近以外的区域.这说明IWO 算法在加强对问题局部搜索能力的同时,也兼顾了全局搜索.
(4)IWO 算法中子代个体分布的标准差随着进化代数而变化,通过对标准差的动态调整,在进化的早期和中期, 生成的群体在加大对优秀个体附近解空间的投点密度的同时, 也兼顾了对优秀个体附近解空间以外区域的搜索.这样群体能保持较好的多样性,可以有效地避免不成熟收敛现象的出现.而在进化的后期, 随着标准差变小, 局部搜索能力不断加强, 算法以更高精度逐步逼近全局最优解.标准差的动态调整是IWO 算法的重要技术环节, 它可以在群体多样性和选择力度之间起到调节作用.
(5)IWO 算法中, 适应度较差的个体也有繁殖的机会,并且与子代个体一起进行竞争淘汰.由于进化算法是一个随机性和再现性的方法, 在演化过程中,有时种群中适应性较差的个体反而比适应性好的个体携带更多有用的信息, 因此就有可能在其子代个体中找到高适应度的个体, 特别是当搜索空间为非线性、非凸时,较差个体所繁殖的子代可能会帮助算法完成突变, 跨过不可行域,这使获得最优解变得更为容易.
综上所述,IWO 算法把进化建立在群体中优秀个体的基础上, 通过标准差的动态调整把局部搜索和全局搜索有机地结合起来.相比于其他进化算法,IWO 算法中的群体只是起到搜索引擎的作用, 优秀个体的进化是基于一定概率规则引导下的一种统计结果.
2.2 IWO 算法马尔可夫链收敛性分析
记IWO 算法的解空间为Ω,解个体为x,x∈Ω,每一代的最优个体记为(t为进化代数, 下同),{ ,t=0 ,1,…}构成了一个离散时间的随机过程.IWO 算法在父代个体的基础上, 通过叠加服从正态分布的随机变量产生下一代群体.记父代群体中的最优个体为(其对应状态为Ei), 子代群体中的即最优个体为(对应状态为E j).显然,此状态转移构成了一个离散的马尔可夫链, 即子代个体的产生只与父代个体相关,而与之前各代的个体无关.由于标准差随着进化代数而动态调整,此马氏链是非时齐的(non-time homogeneous), 即其状态转移概率f(x*)] =1 .与进化代数有关.设为从第t代的状态E i转移到第t+1 代的状态Ej的转移概率.从保留最优个体的角度考虑

定义1 设全局最优解为x*, 如果对于随机过程{ ,t=0 ,1,…},有=f(x*)] =1成立,则称算法以概率1 收敛于全局最优解.
定理1 IWO 算法以概率1 收敛到全局最优解.
证明 如果将群体中的个体按适应度值从大到小进行排列,则IWO 算法的有限状态马氏链第t代的一步转移概率矩阵为
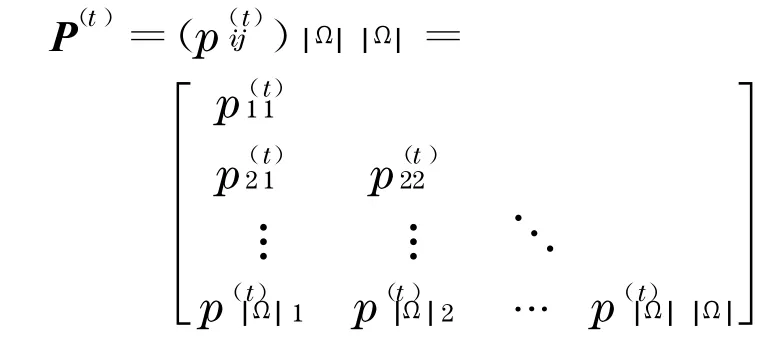
式中,P(t)为下三角矩阵, 其中.记此马尔可夫链的k步转移矩阵为P(k),由马尔可夫链的性质得P(k)=Pk,且P(k)收敛到一个全正稳定随机矩阵=(1 ,1,…,1)T(p1,p2,…,p n),其中(p1,p2,…,p n)惟一满足(p1,p2,…,p n)P =(p1,p2,…,p n)=1,及.即(p1,p2,…,p n)是矩阵P 的特征值为1 且每一分量为正数的左乘特征向量.所以
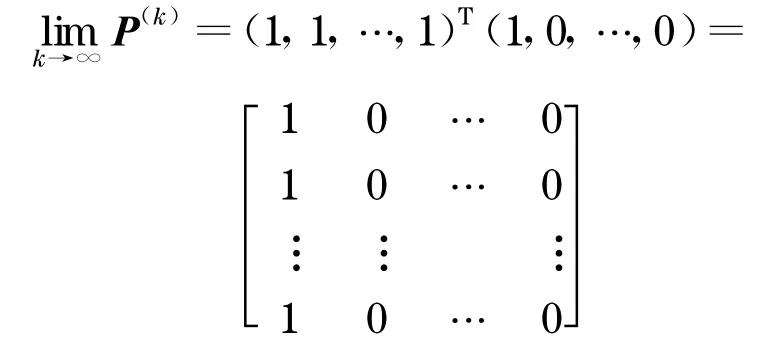
所以,从马氏链的极限分布可以得知,IWO 算法以概率1 收敛于全局最优解,由此定理1 得证.该定理表明, IWO算法进化足够多代数后,群体中的最优个体以概率1 收敛到全局最优解,且从以上证明可以看出, 算法的收敛与初始状态无关.它表示算法经过相当长的时间后趋于平衡状态.这时, 各个解的概率分布既不依赖于初始状态, 也不再随时间的推移而改变.
3 IWO 算法的工程应用
减速器优化设计模型是一个较典型的高维、多约束优化设计问题.图1 是某型减速器结构布置图,优化目标为减速器的体积最小(或质量最轻), 问题的约束是齿的弯曲和接触应力及扭转变形和应力等满足预定值.设计变量:x1为齿面宽度, cm ;x2为齿轮模量, cm ;x3为副齿轮齿数;x4为轴1 上两轴承之间的距离,cm ;x5为轴2 上两轴承之间的距离, cm ;x6为轴承1 的直径, cm ;x7为轴2 的直径,cm .模型的具体推导过程可见文献[6] .

图1 某型减速器结构布置图Fig.1 Structural layout of a type of reducer
代入实际数据后, 此问题可抽象为如下数学模型:
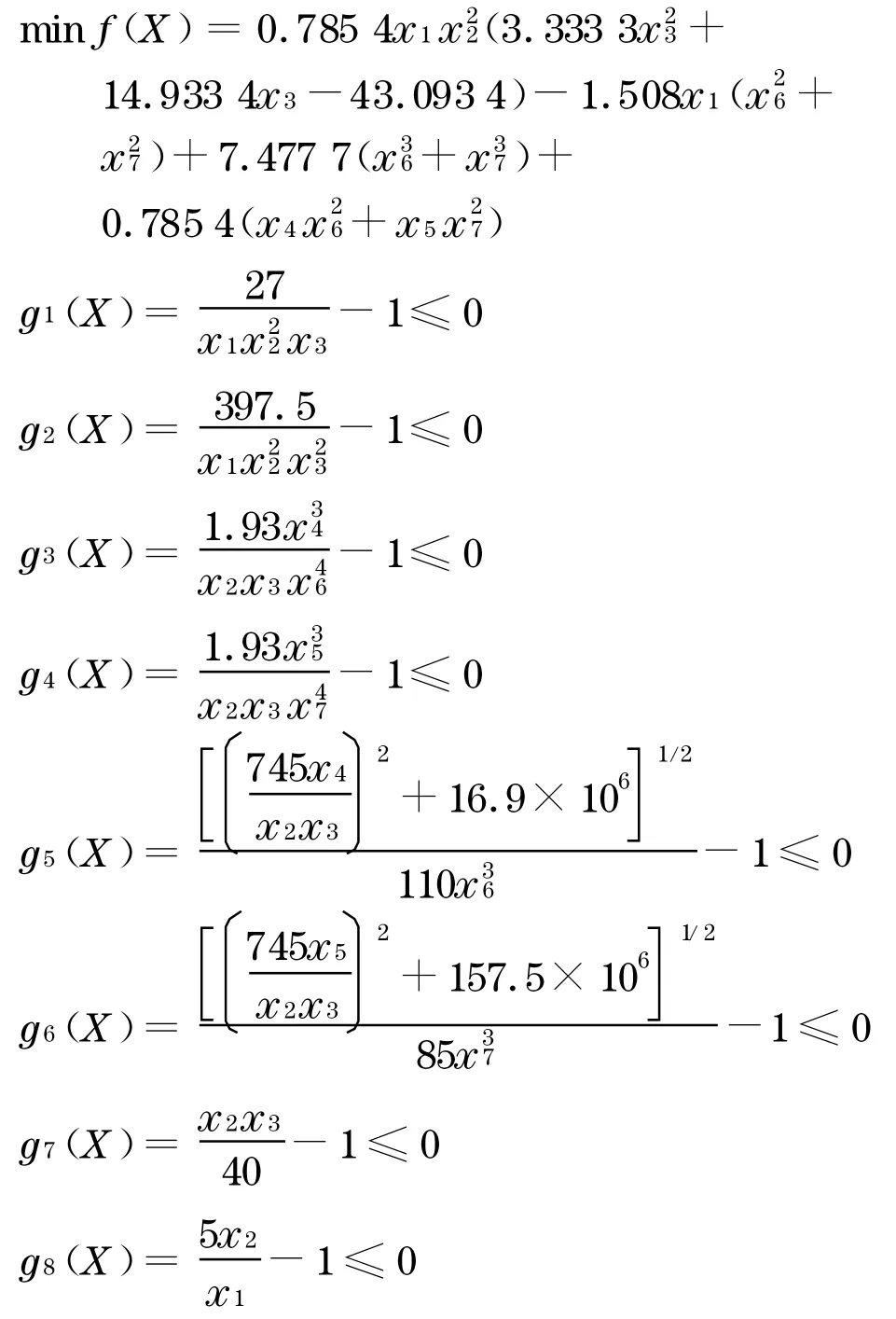

式中:x1,x2,x4,x5,x6,x7为连续变量;x3为离散整数变量.
变量的上下界约束为:2 .6 cm ≤x1≤3 .6 cm ,0 .7 cm ≤x2≤0 .8 cm,17 cm ≤x3≤28 cm,7 .3 cm ≤x4 ≤8 .3 cm,7 .8 cm ≤x5 ≤8 .3 cm,2 .9 cm ≤x6 ≤3 .9 cm ,5 .0 cm ≤x7≤5 .5 cm ,g1(X)~g11(X)是所优化模型的约束函数.
为了研究IWO 算法对工程实例优化的效果, 同样将遗传算法(GA)、蚁群算法(ACO)、粒子群算法(PSO)用于上述减速器模型的优化, 各算法都进化200 代,其余参数设置如下:
GA ——种群大小取40 ,变量编码的二进制位数取25 ,采用两点交叉的方式, 交叉概率取0 .7,变异概率取0 .028 ;
ACO ——蚂蚁个数为40,初始信息素浓度取0 .01 ,信息素挥发系数取0 .99 ;
PSO ——粒子个数取40,惯性权重ω=0 .729 8 ,加速度常数c1=c2=1 .496 2 .
IWO 算法在优化此减速器模型时算法中各参数的设置如下:D=7 ,N0=10 ,pmax=30 ,最大种子数smax=5 ,最小种子数smin=1 ,n=3,初始标准差σini=[1,0 .1,9 ,1,0 .5,1 ,0 .5] ,最终标准差σfin=[0 .1,0 .1 ,0 .1 ,0 .1 ,0 .1 ,0 .1 ,0 .1] .
由于优化算法本身不具备处理约束的能力, 为增加可比性, 在将上述各算法用于本文中减速器的优化时, 一致采用文献[7] 基于可行性规则的约束处理技术来处理约束, 将所求问题演化为一个无约束优化模型,得出的结果列于表1 .

表1 减速器设计优化结果对比Tab.1 Contrast of op tim ization resu lts of the reducer
从表1 可以看出,相比于其他3 个算法, IWO 算法在严格满足约束条件的前提下,得出了更好的解.
4 结论
(1)IWO 算法以群体中优秀个体来指导种群的进化, 以正态分布的方式将子代个体叠加在父代个体周围,通过标准差的动态调整,兼顾了群体的多样性和选择力度.本文通过马尔可夫链的极限分布, 证明算法以概率1 收敛到全局最优解,并用算例与其他智能算法进行了对比.
(2)本文通过将IWO 算法应用于减速器质量最轻数学模型的优化, 对该算法的有效性进行了讨论.结果表明,IWO 算法能够快速、有效地搜索到高质量的优化解, 对于解决工程实际问题具有较大的潜力.
(3)随着函数维数和群体规模的增加, 如何有效缩短算法的运行时间,提高求解精度, 并提高约束优化问题的适应性,为今后的研究方向.
[1] 黄友锐.智能优化算法及其应用[M] .北京:国防工业出版社, 2008.H UANG You rui.Intelligent optimization algorithm s and its application[M] .Beijing :National Defense Industry Press, 2008.
[2] 曹先彬, 罗文坚, 王煦法.基于免疫网络调节的改进遗传算法[J] .高技术通讯, 2000, 10(10):23.CAO Xianbin, LUO Wenjian, WANG Xufa .An im proved genetic algorithm based on idiotypic network regulation[J] .High Technology Letters, 2000, 10(10):23.
[3] 曾渊, 李源, 许家栋.改进微粒群算法在光子晶体优化中的应用[J] .计算机仿真, 2008, 25(3):202.ZE NG Yuan, LI Yuan, XU Jiadong .Improved particle swarm optimization and its application in photonic crystal [J] .Compu ter Simulation, 2008, 25(3):202.
[4] 张志霞, 邵必林.基于改进蚁群算法的运输调度规划[J] .公路交通科技, 2008, 25(4):137.ZHANG Zhixia, SHAOBilin.Vehicle routing and scheduling based on improved ACO [J] .Journal of Highway and Transportation Research and Development,2008, 25(4):137.
[5] Mehrabian A R, Lucas C .A novel numerical optimization algorithm inspired from weed colonization [J] .Ecological Informatics, 2006, 1:355.
[6] Rao S S .Engineering optimization [M] .New York:John Wiley,1996.
[7] Kalyanamoy Deb .An efficient constraint handing method for genetic algorithms [J] .Compu ter Methods in Applied Mechanics and Engineering,2000(186):311.
