采用镜像延拓和RBF神经网络处理EMD中端点效应*

韩建平,, 钱 炯, 董小军

(1兰州理工大学防震减灾研究所 兰州,730050) (2同济大学土木工程防灾国家重点实验室 上海,200092)

引 言

希尔伯特-黄变换 (Hilbert-Huang transform,简称 HHT)在海洋、地震、生物和结构健康监测等领域的应用中显示出了独特的优势[1-4]。 HHT包含两个基本过程:经验模态分解(empirical mode decomposition,简称 EMD)和Hilbert变换。通过 EMD可将复杂信号分解成有限个固有模态函数(intrinsic mode function,简称 IMF)之和,然后对各个 IMF进行 Hilbert变换,研究信号的时频能量分布,得到的Hilbert谱在联合的频率-时间域中描述原始信号具有较高的时频分辨率[5]。国内外学者对EMD边界处理方法作了许多研究,主要有镜像延拓法[6]、神经网络预测法[7-8]、AR预测法[9]、多项式外延法[10]及波形特征匹配延拓法[11]等。

本文选择镜像延拓法和径向基函数(radial basis function,简称 RBF)神经网络预测法作为 EMD中边界处理的方法,对一组简单数值模拟信号和一组 12层钢筋混凝土框架模型振动台试验实测加速度数据进行了处理和分解,并对这两种边界处理方法的效果进行了讨论。

1 端点效应的产生及影响

经验模态分解中,求包络平均是通过对原数据中的上极值点和下极值点分别进行样条插值拟合,然后再平均。在样条插值时,由于端点处极值的不确定性,每一次样条插值都有拟合误差,误差不断累积,分解出来的第l个 IMF端点处会有较大的误差。第 2个 IM F的分解是建立在原始数据减去第 1个IMF的残余项的基础上进行的,由于第 1个 IM F的误差,使残余项也产生误差,导致分解的第 2个 IM F产生更大的误差。依此类推,随着分解的进行,误差就会由端点处向内逐渐传播,最后在严重的情况下会使分解的数据完全失去意义[8]。数值仿真信号的分解可以明显地反映端点效应的影响,如下

如图1所示,该数据序列只存在3个极大值点和4个极小值点,所得上、下包络线均出现失真,尤其是上包络线在信号两端出现巨大的失真。同时,由于数据序列很短,由端点处造成的包络误差已经“污染”到整个数据序列。

图2是未对原始信号x(t)进行边界处理时,通过 EMD得到的各阶 IM F分量与各自对应的真实信号的对比。分解得到的各阶IMF分量与真实信号相比,均出现了偏差,尤其是低频分量,偏差已经非常大,未分解出第3阶分量。由于三次样条插值时需要用到前后各两个临近点,利用三次样条函数进行曲线拟合出现这样的问题是很自然的,解决的惟一途径是在数据序列的两端各增加一个或多个极大值和极小值。

图1 原始数值模拟信号及其上、下包络线

图2 无边界处理的数值模拟信号 EMD分解

2 镜像闭合延拓

根据镜像的对称映射特点,为尽量减少镜像的副作用,将镜子放置在信号具有对称性极值所在位置,首先绘出信号左、右两端的一段曲线及相应的极值,根据曲线的分布特征,决定放置镜子的位置。如在从信号左边起向右的第l个极值处和从信号右边起向左的第r个极值处分别放置两面平面镜,把镜内的信号向外进行映射,得到序列长度为两倍于镜内信号长度的周期性信号。经镜像延拓后的信号不含端点(具有周期性)。由于信号的闭合性,在后续的EMD过程中则不会遇到端点的延拓问题。因此,镜像闭合延拓法可用于处理 EMD的端点效应。

图3为数值仿真信号经过镜像延拓法处理后的EMD结果。可以看出,采用镜像延拓法对原始信号进行处理后可以分解得出3阶 IM F。其中,第 1阶为高频,IMF分量与真实信号偏差很小,基本上与原始信号重合;而后 2阶低频的 IM F分量仍存在一定的偏差,但分解效果明显好于无边界处理时的分解。

图3 采用镜像延拓处理后的数值模拟信号的 EM D

3 基于RBF神经网络的数据序列延拓

采用 RBF神经网络,可以根据整个时间序列的表现特性以及时间序列在端点的具体形式对其加以延拓,在数据两端延拓出极值点。

首先,把相邻的 50个数据作为输入向量,与之相连的1个数据作为输出向量,形成训练样本。本文一共选择了 850个训练样本,将其输入到网络中以训练网络,同时选取预测误差最小的扩展常数来调试网络。图4表明 851个内推值与原始信号基本重合,然后每次将前一次预测的值重新加入网络学习,在此基础上预测后一个值,不断地重复学习预测,最终可以在数据序列的两端延拓出极大值点或极小值点,如图 5所示。

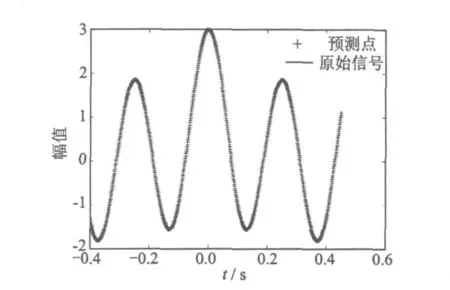
图4 RBF神经网络对数值模拟信号的预测

图5 RBF神经网络延拓后的数值模拟信号

利用基于 RBF神经网络延拓得到的数据序列与原始信号构成一个新的信号,EMD分解过程中得到的包络线如图 6所示。与原信号包络图的对比表明,经 RBF神经网络延拓后,三次样条插值得到的包络图失真现象得到了明显的改善。利用镜像法处理后的分解结果如图 7所示,与图 3相比,较好地分解出了全部 3个 IMF分量,同时各阶 IMF分量与真实信号的偏差明显减小,分解精度大为提高。

图6 经 RBF神经网络预测和镜像延拓处理后信号的上、下包络线

图7 经 RBF神经网络预测和镜像延拓处理信号的 EM D分解

4 结构实测振动信号的处理与分解

选用同济大学土木工程防灾国家重点实验室完成的单跨 12层钢筋混凝土框架模型振动台试验所得的加速度数据作为复杂信号,来验证本文提出方法的有效性。某工况下结构顶层X方向一测点在 El Centro地震波激励下的实测加速度信号如图 8所示[12]。根据 Fourier分析结果,选取合适的带通滤波频率对原始数据进行滤波。滤波后的加速度信号如图 9所示。

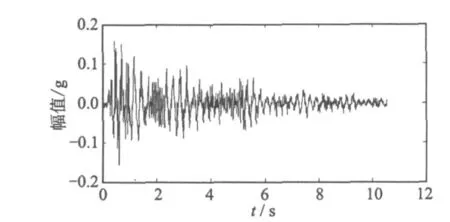
图8 某测点加速度响应原始信号

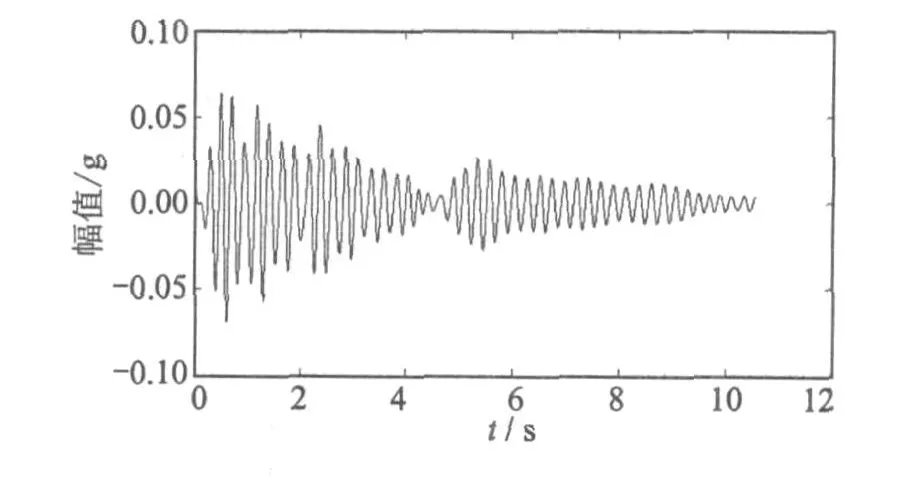
图9 滤波后的加速度响应信号

利用 RBF神经网络对滤波后的信号进行延拓,把相邻的 50个数据作为输入向量,与之相连的1个数据作为输出向量,形成训练样本;选取预测误差最小的扩展常数来调试网络,选择得到2 638个内推值与滤波后的信号基本重合,如图 10所示。基于同样的方法预测出信号前后未知的100个数据,图 11为延拓后的信号。未进行边界处理、直接对滤波后的加速度响应信号的 EMD结果如图12所示。采用镜像法,对经 RBF神经网络延拓后信号的 EMD结果如图13所示。

图10 RBF神经网络延拓后的加速度响应信号

图11 RBF神经网络对滤波后加速度响应信号的预测

图12和图13的对比表明,信号未进行边界处理而分解出来的 IM F分量只有 4个,且各个 IMF分量的端点都有失真的现象;而经过 RBF对信号延拓、再采用镜像法处理后的分解比较完全,一共分解出了7个 IMF分量,端点失真现象明显减弱。

5 结 论

本文在探讨端点效应出现原因的基础上,提出采用镜像法和 RBF神经网络延拓法处理 EMD中的端点效应问题,并利用这些方法对一组数值仿真信号和 12层钢筋混凝土框架模型振动台试验实测加速度记录进行了处理及分解。结果表明,这两种方法基于边界两端预测数据,可以抑制边界效应对分析信号的影响,在一定程度上都提高了 EMD的分解效果。在处理简单周期信号中,利用镜像延拓、RBF神经网络预测或先用 RBF神经网络预测、再采用镜像延拓处理信号都是有效的。对于复杂信号,仅采用RBF神经网络延拓原始信号对减弱端点效应的影响没有明显改进;而对信号经滤波后先利用 RBF神经网络延拓,再利用镜像法进行处理,可以明显减弱端点效应的影响。

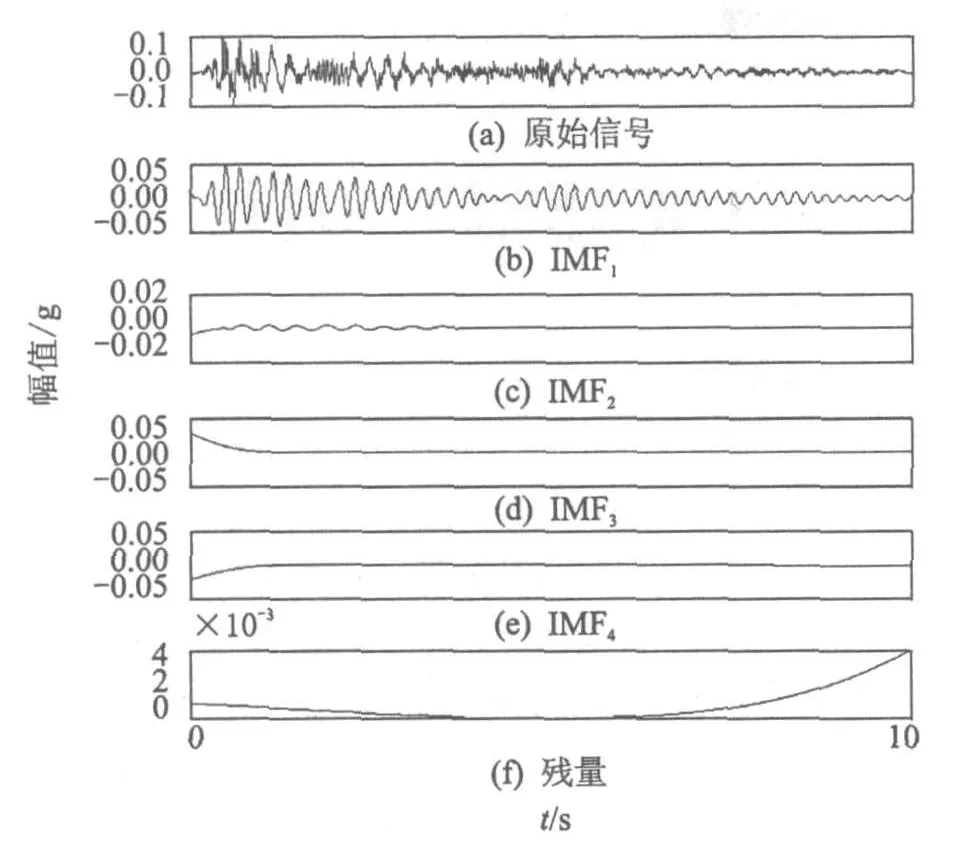
图12 无边界处理的加速度响应信号 EM D分解

图13 经 RBF神经网络预测和镜像延拓处理的滤波后加速度响应信号的 EM D分解

[1] Huang N E,Shen Z,Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A,1998(454):903-995.

[2] Han Jianping,Li Dawen,Li Hui.Modal parameter identification of civil engineering structures based on Hilbert-Huang transform[C]∥Engineering Structural Integrity: Research,Development and Application.Beijing:China Machine Press,2007:366-368.

[3] Yang J N,Lei Y,Lin S,et al.Hilbert-Huang based approach for structural damage detection[J].ASCE Journal of Engineering Mechanics,2004,130(1):85-95.

[4] Rilling G,Flandrin P,Goncalves P.On empirical mode decomposition and its algorithms[C]∥IEEEEurasip Workshop on NonlinearSignal and Image Processing.Grado-Trieste:N SIP,2003.

[5] 胡劲松,杨世锡,吴昭同,等.基于 EMD和 HHT的旋转机械振动信号时频分析 [J].振动、测试与诊断,2004,24(2):106-110.

[6] 黄大吉,赵进平,苏纪兰,等.希尔伯特-黄变换的端点延拓[J].海洋学报,2003,25(1):1-11.

[7] 邓拥军,王伟,钱成春,等.EMD方法及 Hilbert变换中边界问题的处理 [J].科学通报,2001,46(3):257-263.

[8] 瞿伟廉,程磊.应用径向基函数神经网络处理EM D方法中的边界问题 [J].华中科技大学学报:城市科学版,2006,23(4):1-4.

[9] 张郁山,梁建文,胡聿贤.应用自回归模型处理 EMD方法中的边界问题 [J].自然科学进展,2003,13(10):1054-1059.

[11]胡爱军,安连锁,唐贵基.Hilbert-Huang变换端点效应处理新方法 [J].机械工程学报,2008,44(4):154-158.

[12]吕西林,李培振,陈跃庆.12层钢筋混凝土标准框架振动台模型试验的完整数据 [R].上海:同济大学土木工程防灾国家重点实验室振动台试验室,2004.