基于熵权理论的煤矿突发水灾害救援系统可靠性评价*
2010-12-12赵明忠冯立杰王金凤王化强杨林春
赵明忠 冯立杰,2 王金凤 王化强 杨林春
(1.郑州大学管理工程研究所,河南省郑州市,450001;2.河南矿山抢险排水救灾中心,河南省郑州市,450014)
1 煤矿突发水灾害救援系统可靠性评价指标体系的建立
煤矿生产是一个涉及人-机-环境、生产组织方式、工程技术水平等多种要素的复杂半封闭动态系统,煤矿突发水灾害救援系统是这个复杂系统的有机组成部分。笔者根据系统工程的思想,将煤矿突发水灾害救援系统进行分解,同时结合实际救援活动中存在的管理、人员素质、地质环境等影响因素,将煤矿水灾害应急救援系统分为管理手段、人员素质、机器设备、地质环境等4项指标,并将此4项指标进一步分解,建立了矿山水灾害应急救援系统可靠性评价指标体系,见图1。
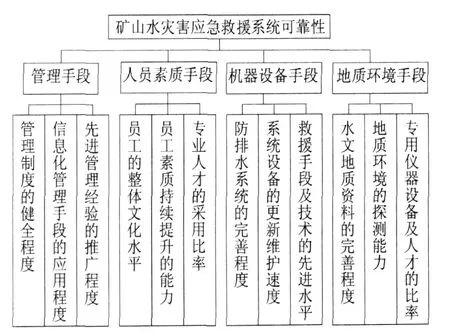
图1 矿山水灾害应急救援系统可靠性评价指标体系
2 基于熵权理论的评价模型
在信息论中,熵值反映了信息的无序化程度,可以用来度量信息量的大小。某项指标携带的信息越多,表示该指标对决策的作用就越大。熵值越小,则系统的无序度越小,故可用熵权理论评价所获系统信息的有序度及其效用。它是通过评价指标值构成的判断矩阵来确定指标的权重,尽量消除在对各层指标进行赋权时存在的人为干扰,从而使评价结果更符合实际。
2.1 建立初始指标数据矩阵
假设突发水灾害救援系统有m个样本煤矿,根据上文所讲的方法可确定动态评价指标集U,将评价指标体系看作一个系统,该系统有l个一级评价指标(子系统),即Ui(i=1,2,…,l)。其中,第i子系统Ui有ni个二级评价指标,即Ui={Ui1,Ui2,…Uini},且=n,设初始的指标数矩阵为:
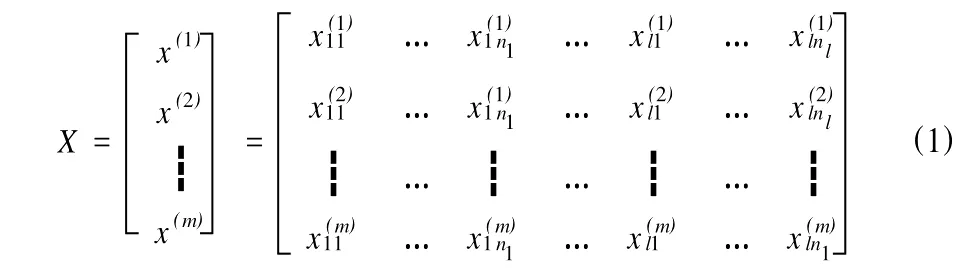
2.2 指标数据矩阵规范化与标准化
由于评价指标的数值具有不同的量纲和数量级,没有可比性,需要做规范化处理。在评价指标体系中主要有极大化指标(越大越优型)、极小化指标(越小越优型)。利用极差变换公式,各类指标规范化公式如下:
极大化指标:
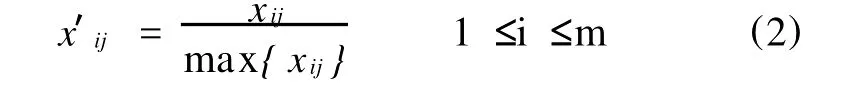
极小化指标:
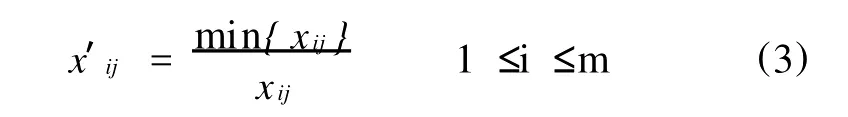
式中,x′ij为规范化后的指标值。标准化公式:
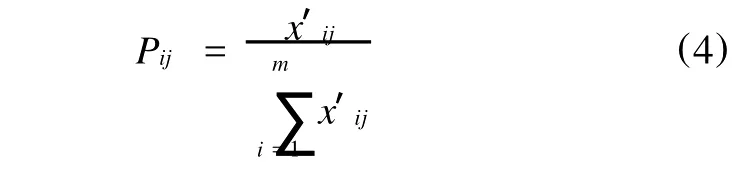
经计算可得数据的标准化矩阵:

2.3 熵权值法确定各级指标权重
2.3.1 计算各级子系统指标的权重
不妨以Ui={Ui1,Ui2,…,Uin}为例,各样本子系统Ui各个二级指标的标准化矩阵为:
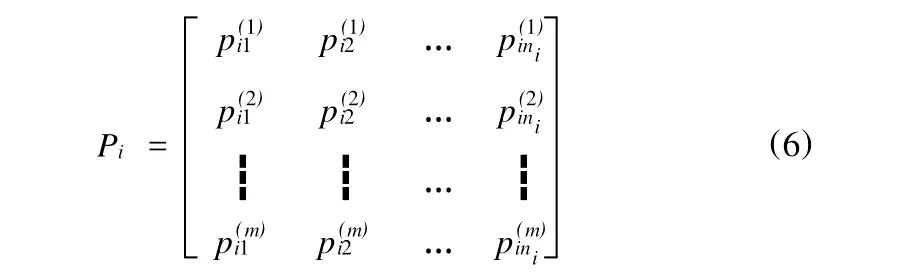
(1)计算第i子系统中的第j项二级评价指标的熵值eij:
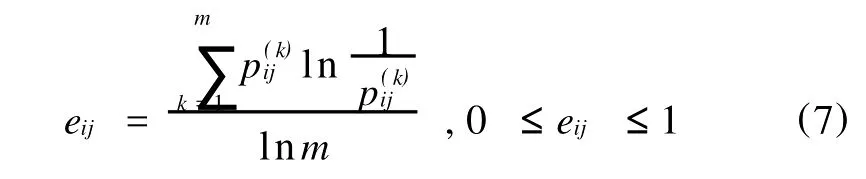
(2)计算第j项指标差异性系数:

指标的差异性系数越大,说明该项指标对评估的重要性越大,影响程度也越大。
(3)利用熵值法确定各项指标的相对权重,即第j项评价指标的权重为:

则子系统各评价指标的熵权向量Hi:

2.3.2 计算系统各层指标的权重
(1)确定第i项一级指标的权重。根据熵的可加性,第i项子系统的差异性系数Gi:
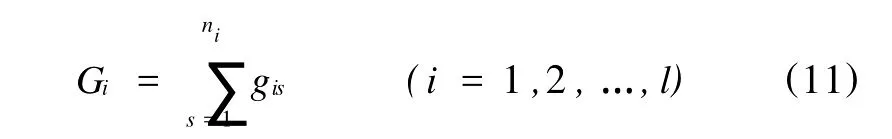
则第i项一级指标的权重为:
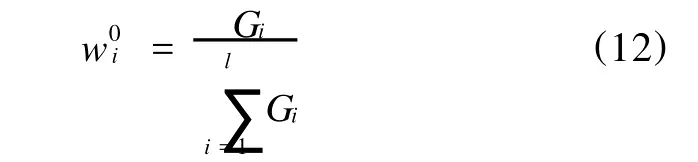
(2)确定一级指标的综合权重。由熵权法确定的指标权重是根据数据之间的关系来确定,可能只反映局部情况,有时与实际情况相差较大,因此需要由实践经验(即专家评判)来进行修正,从而建立熵权和专家评判相结合的综合权重,以尽可能真实地反映实际情况,为决策者提供最准确的决策支持。
综合权重wi的计算公式:
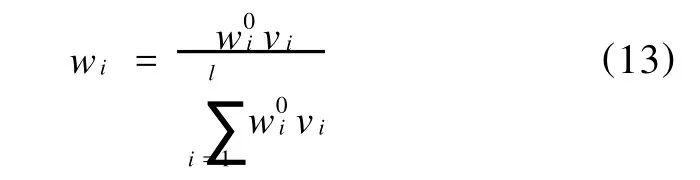
式中,vi——专家评判的权值。
2.4 计算各样本的综合评价值
样本的综合评价值是将熵权法计算出的权重与专家给出的参考权重进行综合得出综合权重,然后乘以各指标的具体指标值,最后得出综合评价值。
由A HP的综合评价值算法可知,第k个样本综合评价值的计算公式为:
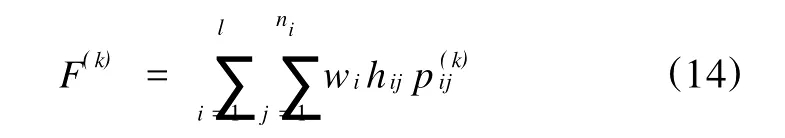
其中,i=1,2,…l;j=1,2,…ni;k=1,2,…m。
3 实证分析
3.1 样本数据的获得
本文矿山突发水灾害应急救援系统选取5个样本,由10个专家组成的专家团对样本系统进行了百分制的打分评判,并对打分结果进行了归一化处理,其数据如表1所示。

表1 样本矿井水灾害救援系统数据表
3.2 计算各级指标的标准化矩阵
各一级指标的标准化矩阵依次为:

3.3 计算各级熵权值及各级权重
参照熵权值的算法可以得到:
指标U1下各个二级指标的熵权值:H1=(0.1803,0.3607,0.4590)。
指标U2下各个二级指标的熵权值:H2=(0.0558,0.7386,0.2026)。
指标U3下各个二级指标的熵权值:H3=(0.8179,0.1450,0.0371)。
指标U4下各个二级指标的熵权值:H4=(0.2222,0.3889,0.3889)。
一级指标的熵权值为:W0=(0.0194,0.0487,0.9090,0.0072)。
专家确定的参考权重为:V=(0.3,0.2,0.35,0.15)。
由公式(13)计算可得综合权重:W=(0.0174,0.0291,0.9503,0.0032)。
3.4 综合评价排序
最后根据公式(14)将上文得出的综合权重与各指标值相乘后加和,可求得各样本救援系统可靠性的综合评价值,如表2所示。
由表2可以看出,样本矿井水灾害救援系统可靠性评价综合排序前三名为矿4、矿3、矿5,而矿1和矿2两个矿井的突发水灾害救援系统可靠性则相对较差一些。而由上文得出的综合权重可知,机器设备的权重最大,其次是人员素质和管理。因此,矿1和矿2在对水灾害救援系统进行改进时,应重点加强硬件因素中机器设备方面的改进,同时注重人员素质的提高和管理方式的改进。
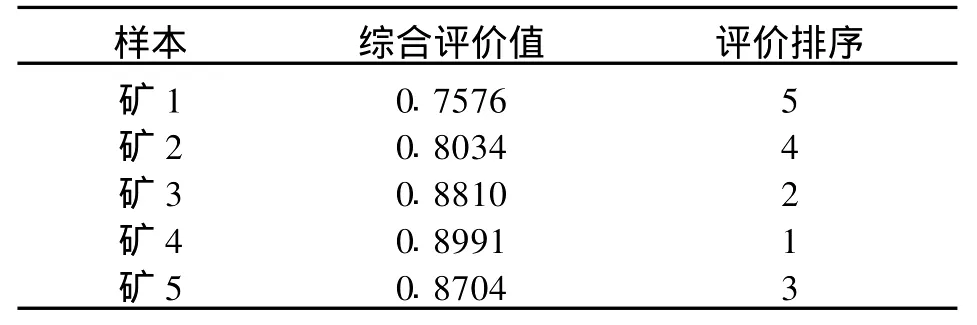
表2 样本矿井突发水灾害救援系统可靠性综合评价表
4 结论
通过实证分析,得出以下结论:
(1)本文遵循全面性、系统性、动态性等基本原则,结合专家咨询意见建立了一套通用的矿山突发水灾害救援系统评价指标体系,并在此基础上根据具体情况对评价指标体系进行动态调整。
(2)引入熵权理论对各层指标进行客观赋权,然后结合专家评价的指标权重进行修正,得出评价指标的综合权重,避免以往煤矿突发水灾害救援系统评价体系中权重获取的主观局限性。
(3)结合样本矿山突发水灾害救援系统实例,计算出各指标的综合权重,区分出指标中的重要因素,依据综合权重对样本矿山突发水灾害救援系统进行了评价排序,并结合评价结果提出了相应的改进措施。
[1] 罗春喜.关于煤矿水害事故原因分析及防治问题的探讨[J].煤炭技术,2006,11
[2] Hawksley J.L.Analysis and assessment of hazards and risks[J].Safety in Chemical Production.Blackwell Scientific Publications,1991
[3] 贺巍巍,郑力,高本河.供应商选择多层次熵权综合评价法研究[J].北京交通大学学报(社会科学版),2007(3)
[4] 罗军刚,解建仓,阮本清.基于熵权的水资源短缺风险模糊综合评价模型及应用[J].水利学报,2008(9)
[5] 李冬梅.铁路隧道风险评估指标体系及方法研究[D].西南交通大学,2008
[6] 汪应洛.系统工程[M].北京:机械工业出版社,2006
