DICM在发动机模态参数识别中的试验研究*

郑 翔,, 高建和, 杨福俊, 阮志强, 何小元

(1扬州大学机械工程学院 扬州,225009) (2东南大学工程力学系 南京,210096)(3扬州柴油机有限责任公司技术开发部 扬州,225006)

引 言

动态位移和频率是分析工程结构和机械装置动力特征的基本参数,是保证施工、运行安全的重要监测量。由于当前工业产品向高速、高性能、高精度和轻结构方向发展,因此,高精度的动态试验分析新方法的研发尤为重要[1-2]。

测量位移、振动频率的常规方法有压电加速度传感器采集信号分析、应变式位移及频率测量系统等。然而,许多动态对象的测试,受现场环境或运行条件所限,常规方法的使用受到限制,如结构工程中测量高耸建筑的上部偏移和风振主频、跨河跨海桥梁施工时结构的位移、旋转体振动频率等;或者受测量对象性质的限制而无法采用接触式方法测量,如传感器安装于轻质、低刚度结构的“附加质量效应”、柔性材料的“强度加强效应”、高温结构的动态变形以及微尺度下构件的力学性能测试等。由于传统方法的局限性和特殊工况,需要有新的测量方法实现和简化动态位移和频率的测量。

高速摄影成像技术[3-5]是研究高速运动过程的一种行之有效的方法,具有很高的时间分辨率,能快速跟踪记录高速运动过程。因此,利用高速摄影成像技术可获取被测对象的瞬间图像,然后采用数字图像相关技术对序列图像进行相关计算,以获得研究对象的位移、速度和加速度曲线,并由此计算振子的固有频率和阻尼系数等动力学参数。该方法对位移的分辨力在亚微米量级,振动频率从低频到高频,甚至上万赫兹,并具有较高的测量精度。数字图像相关方法[6-9]是以图像子区域作为单元通过搜索计算出相关动力学参量,如同在试件上安装没有任何附加质量和附加力影响的“微传感器”。该方法对试件表面要求低,测试结构简单,可用白光作光源;受外界影响小,对隔振条件要求不高;辅之适当的光路,可实现三维振动测量,属于非接触无损全场测量。

本文采用该方法获取了柴油机机体在自由振动状态下各阶固有频率,并与传统的电测值、有限元模拟值进行了比较,验证了整个系统以及数字散斑相关方法用于高速动态测量中的可行性。

1 数字时间序列图像相关方法

1.1 数字图像相关原理

数字图像相关法是一种基于物体表面散斑图像灰度分析,从而获得物体运动和变形信息的新型光测方法,也称为数字散斑相关法 (digital speckle correlation method,简称 DSCM)。基本原理是通过图像匹配的方法分析其研究对象表面变形前后的散斑图像,来跟踪其表面上几何点的运动,得到位移场。由于散斑分布是随机的,散斑图上每一点周围的一个小区域(通常取n×m的小图像,以下称为该点的子图像)的散斑分布与其他点的子图像不一样,有着不同的散斑强度统计特性,如图1所示。当物面因某种物理原因的作用发生微小变形时,可以认为微变形只改变散射基元的空间位置而基本上不影响其散射特性,因而也不影响散斑场的微观结构,这样散斑图上每一点的子图像仅仅随该点作相应的位移。假设变形前物面上的待测点P在变形后位移到了P′点,则变形前散斑图上P点的子图像S就与变形后散斑图上P′点的子图像S′相对应,两者的相关性最高且相关系数最大。因此P′位置可以通过子图像的相关位移搜索找出来,具体做法是在变形后的散斑图上取一系列位置不同的子图像(大小与子图像S相等),逐个与S相关,计算相关系数。所取子图像位置越靠近P′点,则相关系数就越大(相关系数具有单峰性)。使相关系数取得最大值的子图像中心位置就是P′位置,由此即可确定P点的位移,这就是散斑相关法原理,如图 2所示。

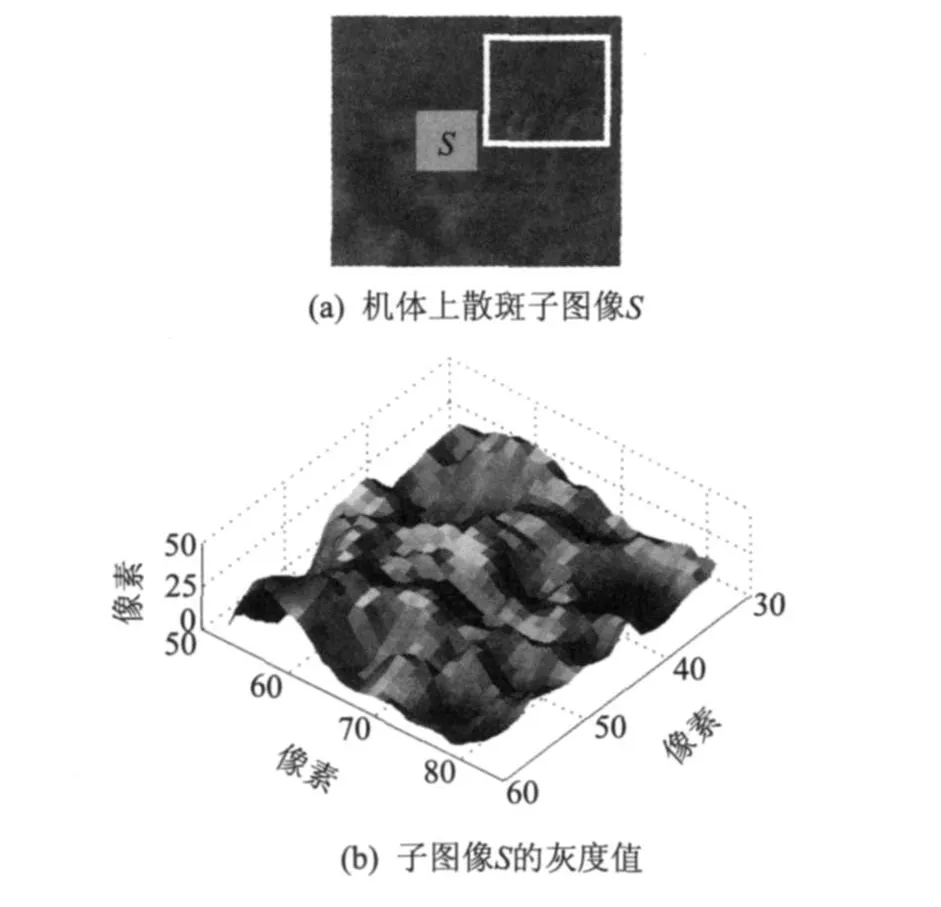
图1 机体上自然纹理散斑灰度图像

在测试过程中,保持光源光照强度和拍摄的位置稳定,则同一点在运动过程中保持相同的灰度I(或颜色 )

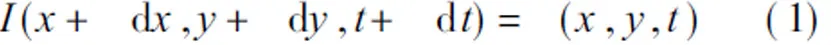
在此条件下,由概率论和统计理论,子集S和子集S′的相关系数C可定义为

其中:f(xi,yj)和g(xi+u,yj+v)为物体运动前后数字散斑图像中各像素点的灰度值;f=为运动前子集S的灰度平均值;为变形后子集S′的灰度平均值。

通过搜索相关系数C,从而实现将变形测量问题转化为一个相关搜索和数字图像识别的计算过程。由式(2)进行相关搜索得到的位移是像素的整数倍,通过整数像素的灰度值内插可求得亚像素或更高精度的位移[10]。文献[10]总结了几种确定亚像素位移的方法。因此,只要能在相关计算中使位移试探增量不超过 0.01像素,利用宽度方向像素为1 024的CCD,位移识别的灵敏度可达 0.098μ m。

1.2 时间序列动态散斑相关跟踪法

从以上原理可以看出散斑相关法只能测量微小的变形或位移,因为当变形较大时会改变散斑场的微观结构,导致子图像S与S′的相关性变差。变形越大,S与S′的相关性越差,相关系数越小,相关系数的单峰性也越来越不明显。同时在主峰的周围出现较大的次峰,有时甚至出现次峰比主峰还高的情形,这时进行相关峰搜索就会出现误判,得出错误的测量结果。大量试验表明,当变形不超过10个像素时散斑相关法的准确性较高,当变形大于10个像素时用散斑相关法测量就不太可靠了,因此一般数字散斑相关法的测量范围约为0.01～10个像素,超出此范围的变形被称为大动态范围的变形。

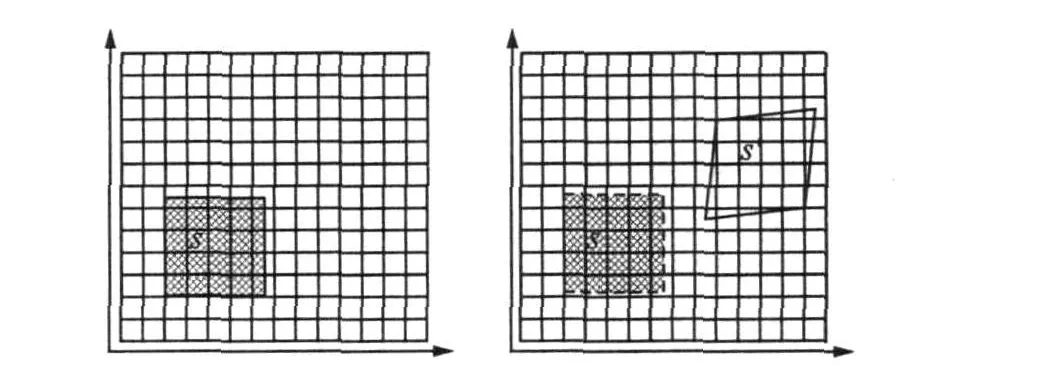
图2 相关搜索的示意图

为了能在散斑相关法的基础上测量大动态范围的变形,在物面发生变形的整个过程中控制摄像机每隔Δt就拍下一张散斑图,时间间隔Δt的选择原则是在Δt时间内,物面的最大变形不超过 10个像素,以保证每相邻两幅散斑图的微观结构基本不变,保持较高的相关性。变形越快Δt就应越短,在试验中要控制好摄像机的拍摄速度。

假设物面变形的持续时间为T=(n-1)Δt,则共需拍摄n幅散斑图f1,f2,… ,fn(变形越大n也越大),如图3所示。这n幅散斑图称为时间序列动态散斑图,可用一般的散斑相关法跟踪待测点的移动踪迹,最终得出测量结果。具体跟踪过程如下:a.取出散斑图f1与f2,在第 1幅散斑图上选取待测点P1(x1,y1),利用散斑相关法找出待测点P1,经过Δt时间移动到了P2(x2,y2),位移为Δx1=x2-x1,Δy1=y2-y1;b.取出散斑图f2与f3,在动态散斑图f2上以P2(x2,y2)为新的待测点,利用散斑相关法找出待测点P2,经过Δt时间移动到了P3(x3,y3),位移为Δx2=x3-x2,Δy2=y3-y2;跟踪待测点P1经过2 Δt时间移动到了P3点。依此类推,逐步跟踪待测点移动的踪迹。经过以上步骤可以跟踪到待测点P1经过T=(n-1)Δt时间 ,依次经过P2,P3,… ,Pn-1点 ,最终移动到Pn点。根据试验需要,可以求出相邻两幅图的位移,也可求出总的位移

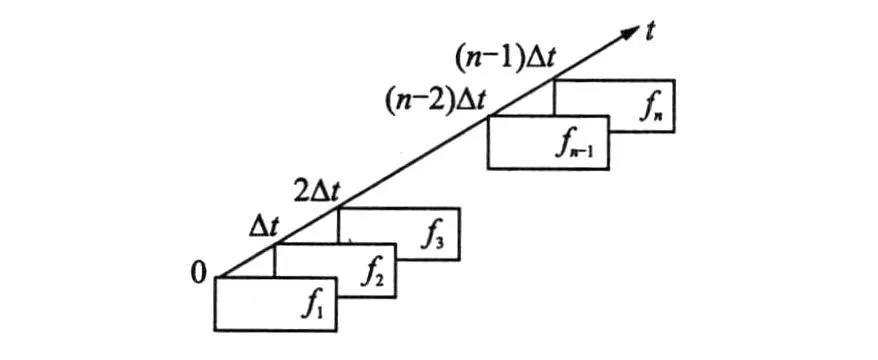
图3 时间序列动态散斑图

通过编程,可使上述散斑相关跟踪测量分析过程全部由计算机自动完成。

本文所研究的动态问题通常是无法进行实时分析的,整个测试过程是:由高速摄像机 CCD记录反映研究对象表面不同动态变形状态信息的序列散斑图,经数字化后,转换成数字图像输入计算机中存储,然后进行相关计算和分析。

2 试验过程及数据处理

2.1 发动机光学测试结果

本文以某型号四缸柴油发动机机体为研究对象,试验时用高速摄像机连续摄取激振时机体测试区域的图像,通过时间序列图像相关方法获取位移-时间曲线,应用加窗(Hamming)傅里叶变换,获取位移-时间曲线的频谱图,从而得到机体自由状态下的各阶固有频率,试验装置如图4所示。

图4 发动机试验装置

本试验测试系统的测量指标如下:位移测量精度达 0.1μm,动态图像采集速率最高为 32 000幅 /s,试验中分别采用的图像采集速率为 8 000幅 /s和4 000幅 /s,测量结构振动上限频率为 4 000 Hz和2 000 Hz。对于稳定振动问题,可选择数个周期内的图像进行分析。试验时用弹性绳将机体悬挂(单点独吊)在固定支架上,使机体处于自由状态。自由模态试验时,一般将悬挂点选择在振幅较小的位置,最佳悬挂点应该是某阶振型的节点[11]。本次试验悬挂点选择在一阶振型的节点处。针对各阶振型(由有限元模拟可知),设计相应测试工况。为使研究对象保持稳定,采用激振器对机体沿x,y,z3个方向分段扫频激励,如沿x向给定0～650 Hz范围扫频激励。将信号发生器产生的、在某变化范围内的谐振信号,经功率放大器放大后输出给激振器。测试点所得到的信息要求有尽可能高的信噪比,因此测试点不应靠近节点。调整激振器的激励位置和相应图像采集位置,反映出不同方位上的振动响应,确保机体在有效激励作用下,产生与各阶固有频率相对应的振动。光源采用冷光源,这种光源通过光纤将光从发光点引到机体表面,从而避免热引起物面变形。摄像机光轴垂直物面,采用机体自然纹理灰度图像,再以8 000幅 /s图像采集速度采集一个扫频周期内测试区域的连续图像,利用时间序列图像处理技术获得测试区域内某点的振幅-时间曲线,如图 5所示。对振幅-时间曲线作一维傅里叶变换获得振动频谱图,如图6所示。对各个扫频段重复4次测试,取均值,计算结果见表1。

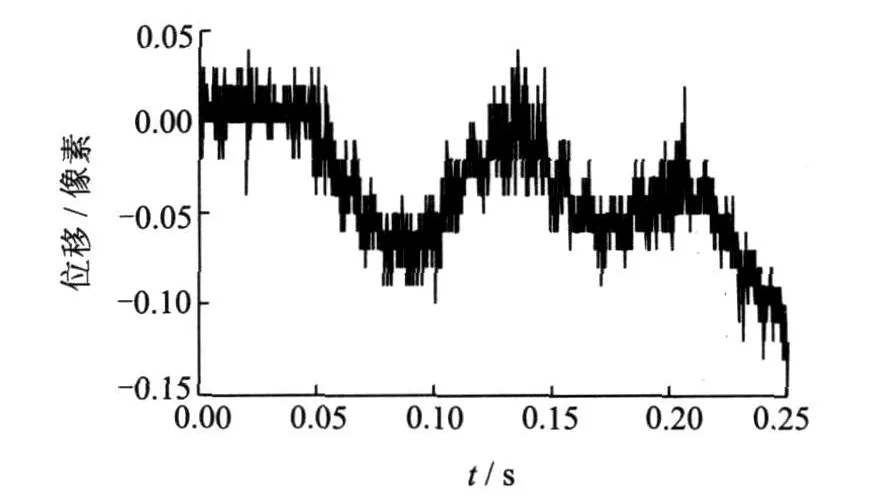
图5 发动机振动时振幅-时间曲线

图6 振幅-时间曲线的频谱分析图

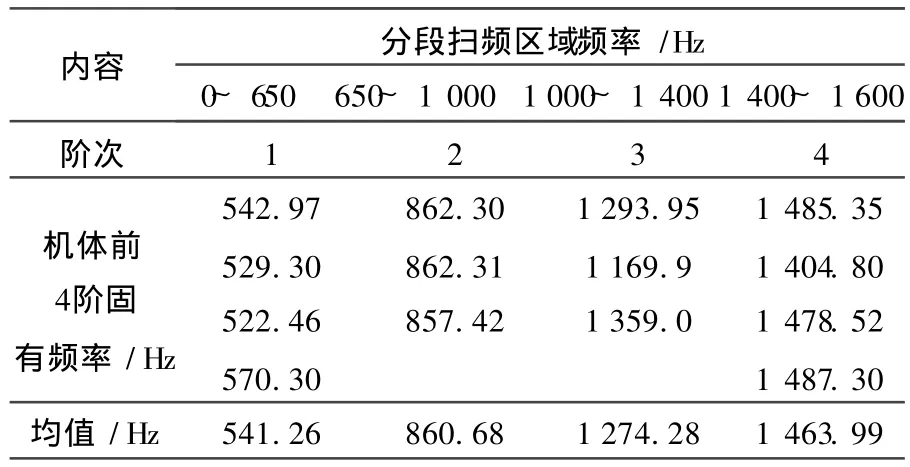
表1 发动机前 4阶固有频率光测试验值

2.2 发动机电测试验结果

为了验证本文的方法,同时还做了传统的电测试验[12-13]。在机体的特征部位装上压电式加速度传感器,采用单点激励,多点拾振,即在机体上多处布置加速度传感器,分别对发动机机体某一部位进行多次瞬时单点敲击,在0～2000 Hz频率范围内分段扫频两种不同形式的激励方式进行激励测试。通过固定在机体上的加速度传感器测出机体在激励情况下的振动加速度波形,如图7所示。然后对振动波形进行频谱分析,从而获得发动机机体的各阶固有频率,如图 8所示。

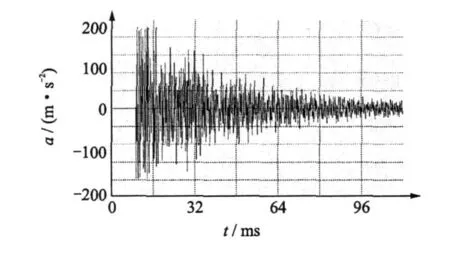
图7 锤击下机体振动波形图

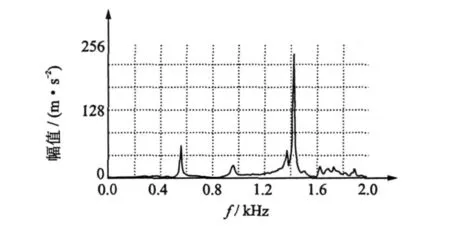
图8 由图7得到的振动频谱图

图8中的各峰值对应的频率即为机体的各阶固有频率。从图中可以看出,前几阶峰值明显,是机体的低阶主振型频率,后面较多的小凸峰为机体的局部高阶频率。表 2为分别采用敲击法和扫频法测得机体前4阶固有频率。多次重复试验,取均值为该柴油机的固有频率值。从表3可以看出,光测值和电测值相当吻合,第1阶固有频率误差仅1.56%。二阶频率光测值误差较大的原因在于拍摄面的选取有角度,测试时要注意光轴垂直被测物面。

2.3 有限元数值模拟

由于柴油发动机机体的结构比较复杂,考虑到ANSYS的建模能力有限,因此,采用了 Pro/Engineer软件建立几何模型。通过Pro/Engineer与ANSYS的无缝接口,将几何模型导入到 ANSYS中。所有的模型特征尺寸均按图纸上的名义尺寸进行创建,不考虑铸造或机械加工的偏差。采用精细建模,利用 Pro/Engineer检查短边的功能,检查模型中存在的短边,并适当地修改模型,消除短边。短边长度定为2 mm,小于2 mm的线尺寸需修改。

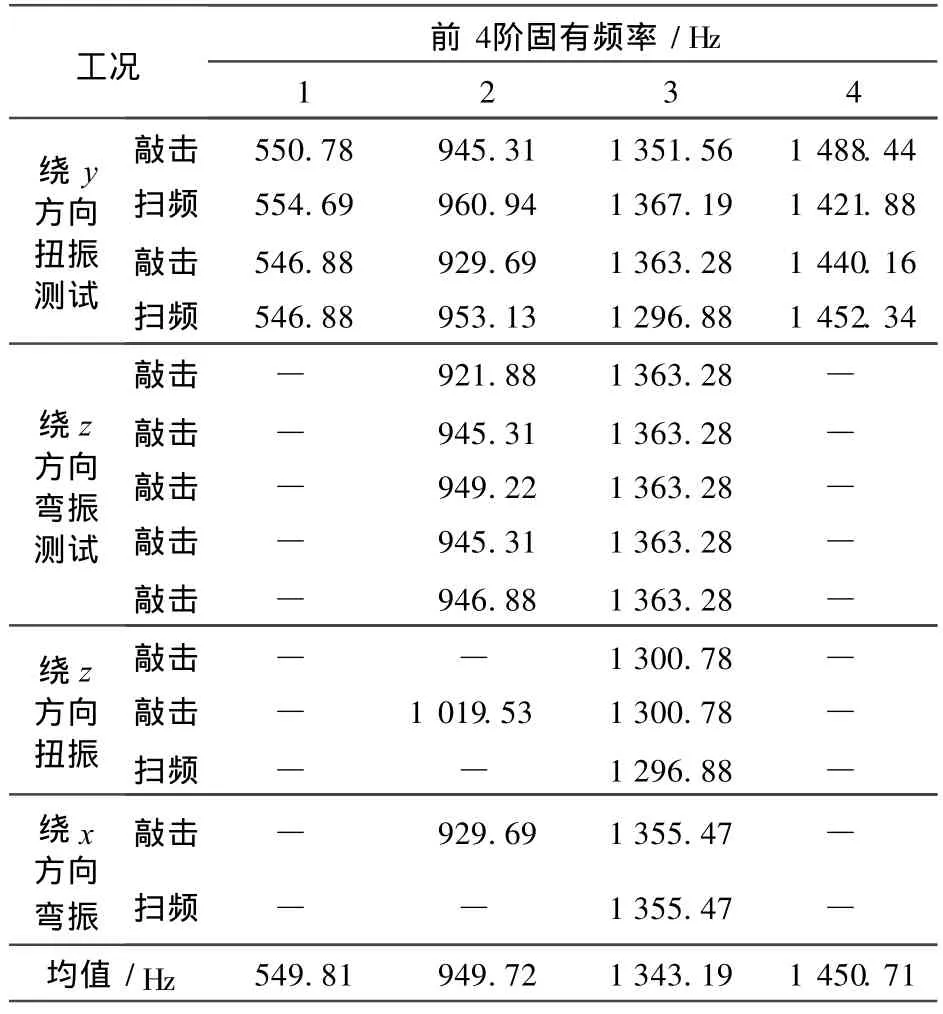
表2 发动机前 4阶固有频率电测试验值

表3 发动机前4阶固有频率光测与电测试验值比较

综合考虑机体结构的特点和计算机的计算能力,忽略了不起主要作用的倒角和过渡圆弧,略去了发动机缸体内小于 6 mm的细小油道孔和左右两侧的水泵壳、齿轮室和飞轮壳的螺栓孔,其余螺栓孔用圆孔代替。材料弹性模量和密度通过样本试件实测得到,分别为 105.75 GPa和 7.466×10-6kg/mm3,泊松比为0.27。有限元模型采用SOLID45三维实体单元进行网格化。为保证网格不发生过大的稀疏变化,以 4 mm单元边长进行全局控制,最终的机体有限元模型共划分了75 318个单元,如图9所示。将光测试验值与有限元模拟值进行比较,从表 4可以看出,光测法和有限元值也相当吻合。

图9 机体的有限元模型

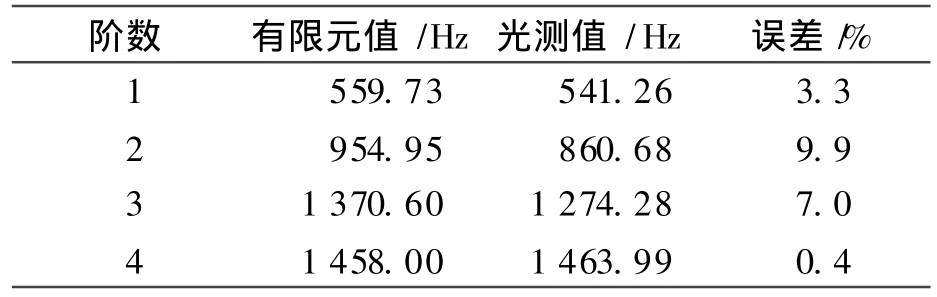
表4 发动机前 4阶固有频率光测试验值与有限元值比较

3 结 论

(1)本文基于高速摄影成像技术,结合时间序列图像相关方法测得了四缸柴油发动机机体在自由振动状态下的位移响应信号,后处理中采用傅里叶变换提取相应的模态参数。基于VC平台编制了数字时间序列图像相关软件,其中相关公式采用平方形式,搜索策略基于时间序列图像的相邻相关。试验结果表明,本测试方法试验装置简单(若测试频率较低,可采用普通的 CCD摄像机或数码相机;若高频测试可采用高速摄像机,根据结构变形的大小调节拍摄时间),测试原理简单,全场非接触,无附加质量,无附加阻尼,测量频率和位移范围可调,可高精度识别系统的模态参数,从而为工程结构和机械产品的动力学参数识别提供了新的测试方法。

(2)时间序列动态散斑相关跟踪法是测量分析面内大变形的有效方法。在大位移测量中,测量上限几乎没有限制。此外在拍摄时间序列散斑图时记下了时间参数,使该法特别适合于测量分析面内动态变形位移和变形速度、加速度。

(3)通过试验模态分析和有限元模态分析,两种情况下的模态参数(固有频率)相对误差很小(1阶频率 3.3%,2阶频率 9.9%,3阶频率 7%,4阶频率0.4%),满足工程要求,说明所建立的机体结构的有限元模型是可行的。

(4)通过光测和电测两种试验方法所获得的数据比较,结果相当吻合。两种试验方法的相互验证,说明了本次试验方法的正确性和获得的试验数据的可靠性。作为一种非接触的位移传感技术,本文方法不受测试环境影响,如高温等。本文侧重于验证该方法对机械结构在复杂环境下动态性能测试的可行性与精度。

[1] 陈徐均,林铸明,吴广怀,等.通载浮桥动态位移的测试方法与数据分析 [J].振动、测试与诊断,2006,26(2):97-101.

[2] 马建仓,石庆斌,程存虎,等.航空发动机转子振动信号的分离测试技术 [J].振动、测试与诊断,2009,29(1):1-4.

[3] Rembe C,Tibken B H E P.Analysis of the dynamics in microactuators using high-speed cine photomicrography[J].Journal of M EM S,2001,10:137-145.

[4] 杨福俊,孙伟,蒋明,等.基于高速图像采集与时间序列图像相关的微陀螺动力学特性测试[J].计量学报,2006,27(4):347-351.

[5] 郑翔,杨福俊,裘安萍,等.双线性振动微陀螺特征频率光学测试和有限元分析 [J].工程力学,2009,26(3):195-201.

[6] Peters W H,Ranson W F.Digital imaging techniques in experimental stress analysis [J].Optical Engineering,1982,21(3):427-431.

[7] Chu T C,Ranson W F,Sutton M A,et al.Applications of digital-image-correlation techniques to experimental mechanics[J].Experimental Mechanics,1985,25(3):232-245.

[8] SchreierH W.Investigation oftwo and threedimensional image correlation techniques with applications in experimental mechanics[D].USA:University of South Carolina,2003:1-4.

[9] 马少鹏.数字散斑相关方法在岩石破坏测量中的发展与应用 [D].北京:清华大学,2003:2-6.

[10]孟利波,马少鹏 ,金观昌.数字散斑相关测量中亚像素位移测量方法的比较 [J].试验力学,2003,18(3):343-348.

[11]袁爱民,戴航,李延和.EI法和 M AC法在模态试验传感器优化布置中应用比较[J].工业建筑,2008,38:343-347.

[12]魏涛,刘涛,石秀勇,等.多缸柴油机机体结构有限元模态分析[J].内燃机与动力装置,2006(4):6-10.

[13]宫文龙,王峰,荣晓明.某柴油机机体模态测试及分析[J].机械工程与自动化,2007(2):112-116.