基于CZT的频率细化方法的FPGA实现
2010-12-03王磊磊
王磊磊, 陈 潜
(上海无线电设备研究所,上海200090)
0 引言
在短持续信号处理中,由于采样点数有限,如何提高频率分析精度一直是数字信号处理研究中的重点。典型的频谱细化分析方法有频率插值法、全相位 FFT法、Zoom FFT法、CZT 法等[1]。其中,频率插值法提高频率分辨率精度有限;全相位FFT法适用于相隔较大的多频率成分离散频谱;Zoom FFT法是通过复调制和低通抽取采样实现的,适用于细化倍数较低的场合;CZT法能充分利用所采集的数字信号,在折叠频率内任何窗口都能以任意选定的频率分辨率进行频谱细化分析[2]。
传统DSP实现CZT方案具有计算时间长、需大存储空间、参数调整不方便等缺点。为解决这个问题,可利用FPGA器件内部包含丰富的硬件资源(如乘法器资源)和开放式IP(如DDS核)方便快捷地实现CZT。本文使用的FPGA芯片为Xilinx公司生产的XC3SD1800A。
1 CZT算法
1.1 CZT算法原理
设AD采样信号为x(n),它的Z变换为
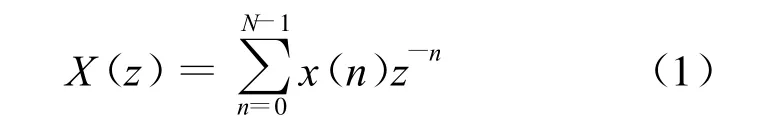
在Z平面内,变量z可以沿更一般的路径取值[3],设z的取样点为
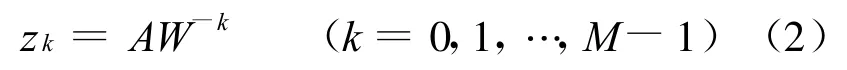
式中:M为要分析的复频谱点数,可不等于N;A和W是任意复数,可表示为
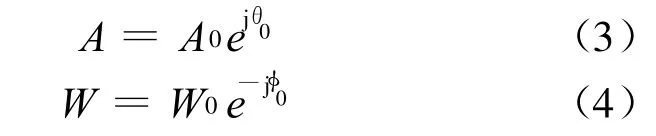
将式(3)和式(4)带入式(2),可得
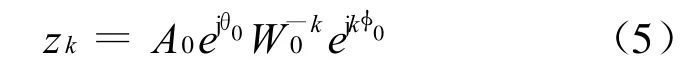
式中:A0为起始取样点z0的矢量半径长度,CZT中A0=1,表示在单位圆上取值;θ0为起始取样点z0的相角,即选取频率范围的起点;φ0为两相邻zk点之间角频率差,即选频范围内的频率分辨率。W 0=1,使得计算周线在单位圆上进行;M=N,使得CZT便于计算。所以,通过调整 θ0来确定选频范围的起点;通过调整φ0来确定选频范围内频谱细化倍数。将式(2)带入式(1),可得
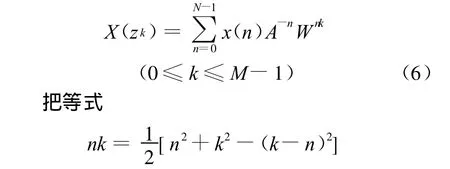
代入式(6),可得
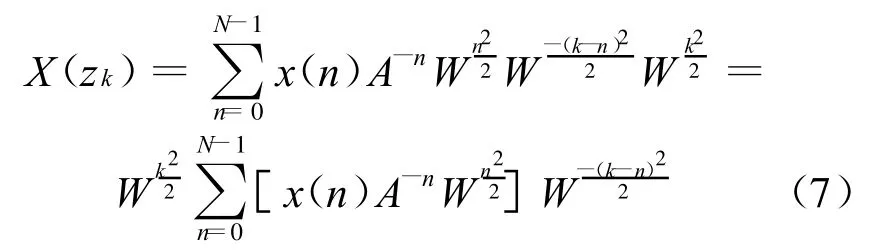
设
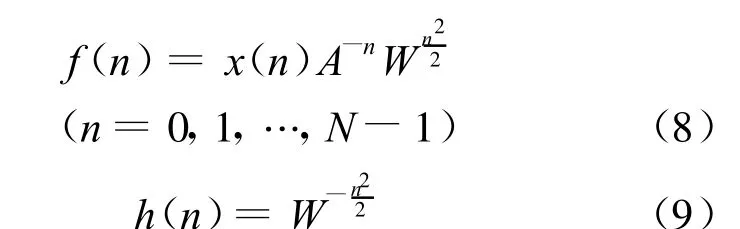
则式(7)可变为
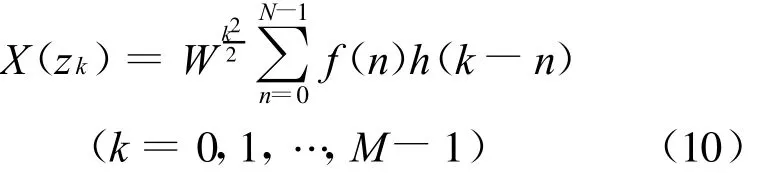
式(10)可用图1来表示。
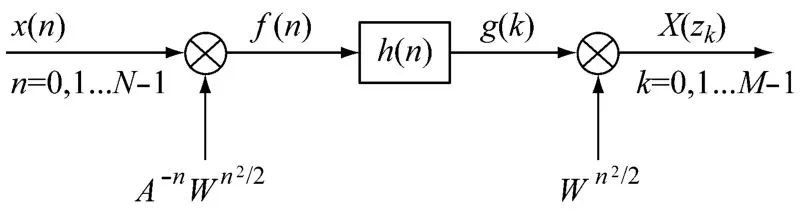
图1 CZT的系统框图
其中:f(n)与h(n)的离散卷积可用 f(n)与h(n)的适当段的圆周卷积来表示。
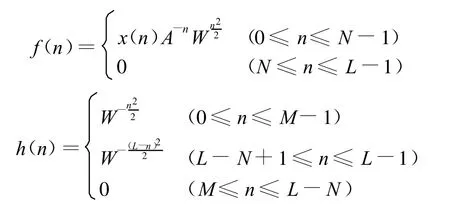
有限长序列的圆周卷积可采用FFT快速计算,如图2所示。
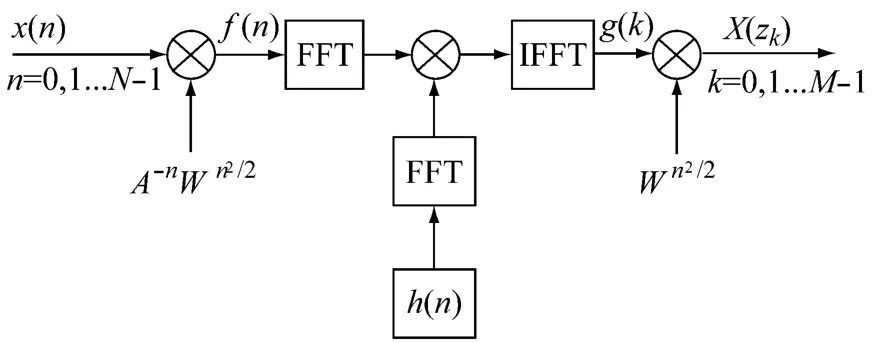
图2 利用FFT计算圆周卷积的CZT框图
1.2 CZT算法特点
基于CZT的频谱细化方法适用于采样点数固定,细化倍数和选频范围可调的应用场合。对由于栅栏效应引起的测频误差采用CZT进行细化可达到较高的频率分析精度,但是对于谱线之间干涉较严重的情况,采用CZT进行细化效果有限,此时只有增加采样点数,获得更高的原始频率分辨率,再进行频谱细化[4]。
2 CZT算法的FPGA实现
2.1 CZT算法FPGA实现构架
从图2中可看出CZT的计算过程包含三个FFT模块和三个复数乘法模块。另外W exp(n2/2)为线性调频信号,可由DDS产生。FFT模块、复数乘法模块以及DDS模块均可以通过调用FPGA的IP核实现,如图3所示。选频范围的起始频率及频率细化倍数可以通过设置DDS模块的参数来确定。
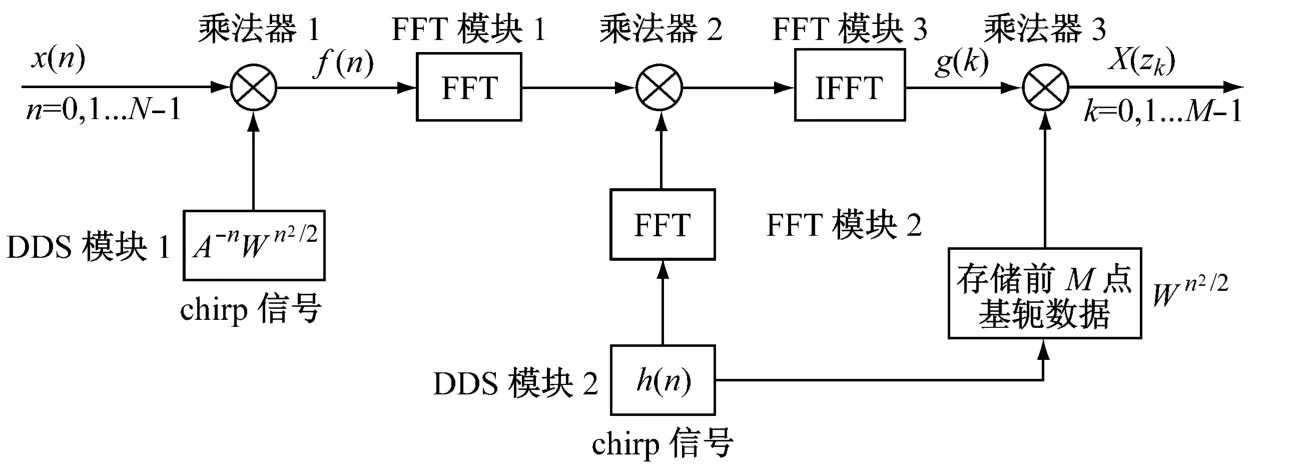
图3 基于FPGA硬件实现CZT的结构框架
为提高算法的计算时间,DDS模块1可与DDS模块2并行运行;FFT模块1可与FFT模块2并行运行。所有模块均采用3级流水线的工作模式[5]。
为节省芯片资源,乘法器1可复用;FFT模块1可与FFT模块3复用。这样采用FPGA实现一个CZT仅需要二个DDS模块、二个FFT模块、一个复数乘法器模块便可完成,如图4所示。
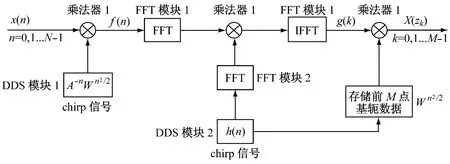
图4 资源复用后的CZT结构框架
2.2 FPGA实现CZT的时序框架
从图4看出,自DDS模块1启动经过复数乘法器1,再经过FFT模块1到达复数乘法器1的输入端的时间,要比自DDS模块2启动经过FFT模块2到达复数乘法器的输入端的时间长。为使两条支路时间一致,在DDS模块2和FFT模块2之间加入一级缓存,如图5所示。
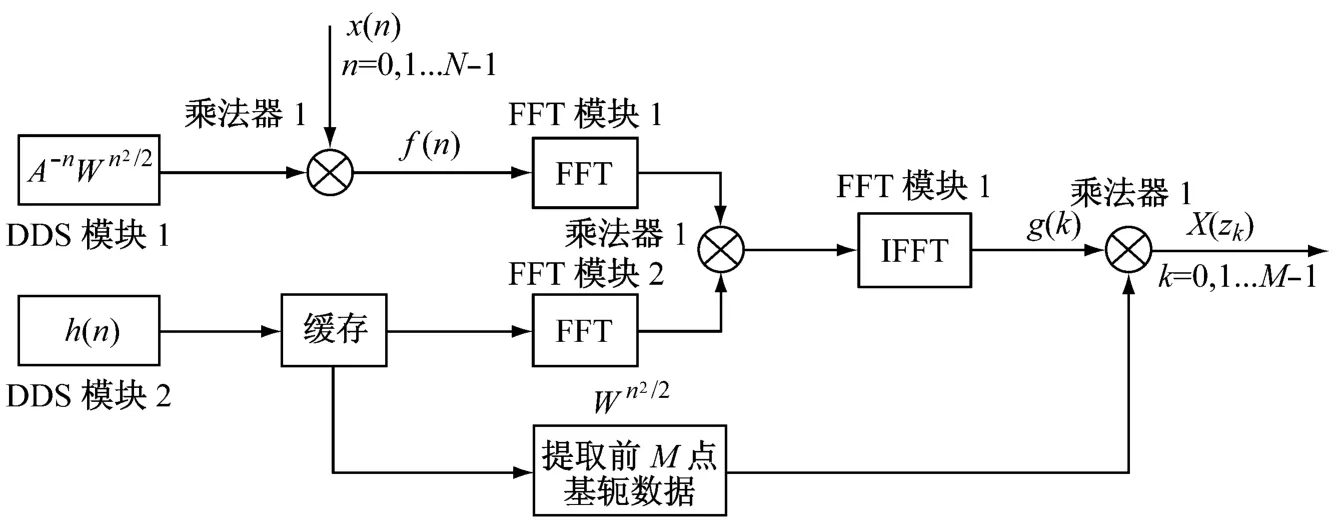
图5 基于FPGA硬件实现CZT的时序框架
2.3 与DSP实现CZT方案的比较
传统采用DSP实现CZT中,需要大量的空间存储线性调频信号W exp(n2/2)。另外,由于DSP芯片自身乘法累加器资源有限,所有的运算只能顺序执行,这就造成计算时间长,给工程应用带来了巨大的障碍。当采用FPGA后,系统结构清晰,运算时间大幅缩短,参数调整灵活。分别使用TI公司的 TMS320F2812芯片和Xilinx公司的XC3SD1800A芯片实现CZT计算时间,如表1所示。
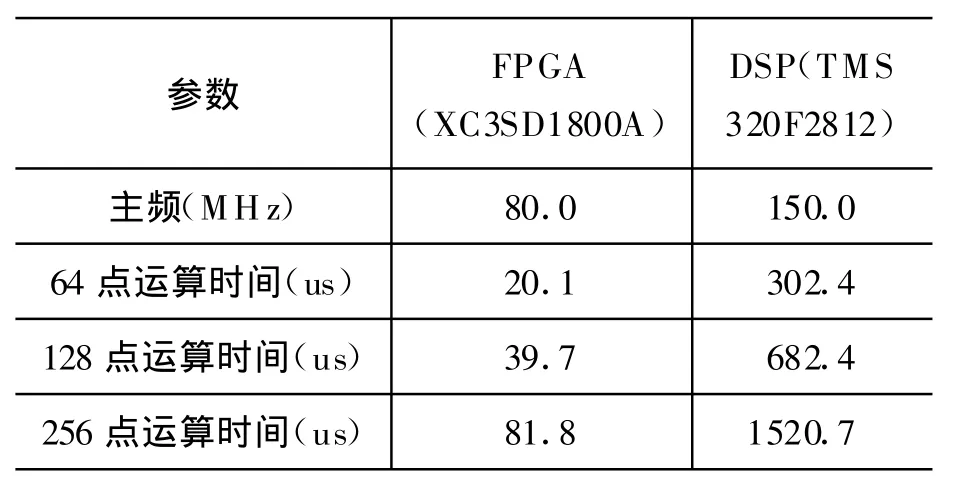
表1 FPGA与DSP实现CZT运算时间
从表1可以看出,尽管FPGA主频是DSP主频的一半,但是其计算时间是DSP计算时间的1/15。
一个XC3SD 1800A芯片实现的、可配置点数(32点至512点)、可配置细化功数字频率区间(0至2π)、8倍细化的CZT模块占用资源,如表2所示。
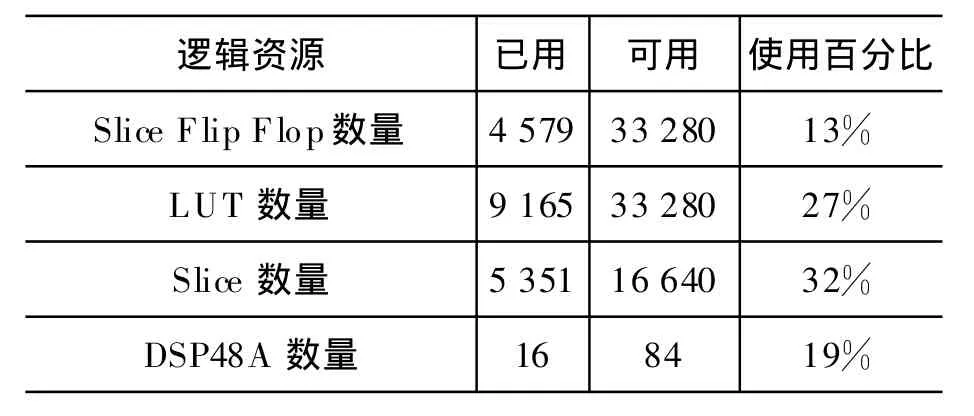
表2 CZT模块占用资源表
XC3SD1800A是Xilinx嵌入有乘法器核的产品中资源最少的芯片。从表2看出,LUT使用率仅为27%,Slice使用率仅为32%,DSP48A使用率仅为19%。
2.4 试验验证
图6、图7为采样率为100 kH z,采集频率为24.219 kHz的数字信号。图8为对时域进行64点FFT的计算结果。图9为对图8中虚线部分内的选频范围进行8倍细化的CZT结果。所有计算均在FPGA芯片(XC3SD1800A)内部完成。FFT计算的频率为25 kH z,计算误差为0.781 kHz;CZT计算的频率为24.21875 kHz,计算误差为0.00125 kH z。
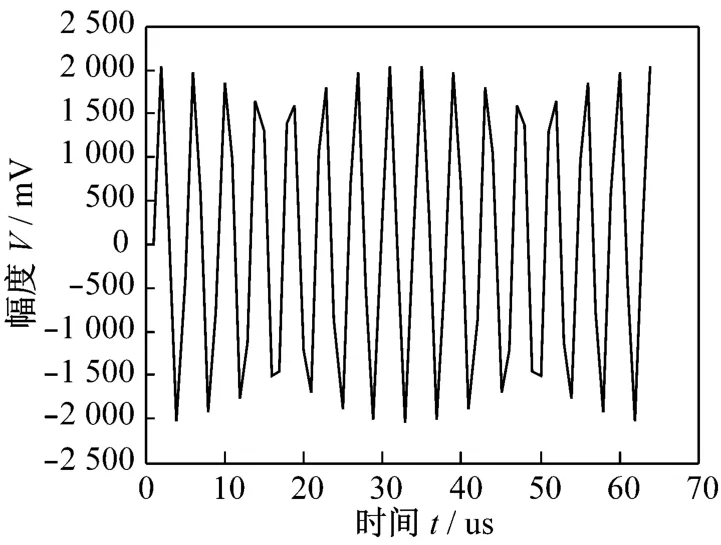
图6 输入信号实部
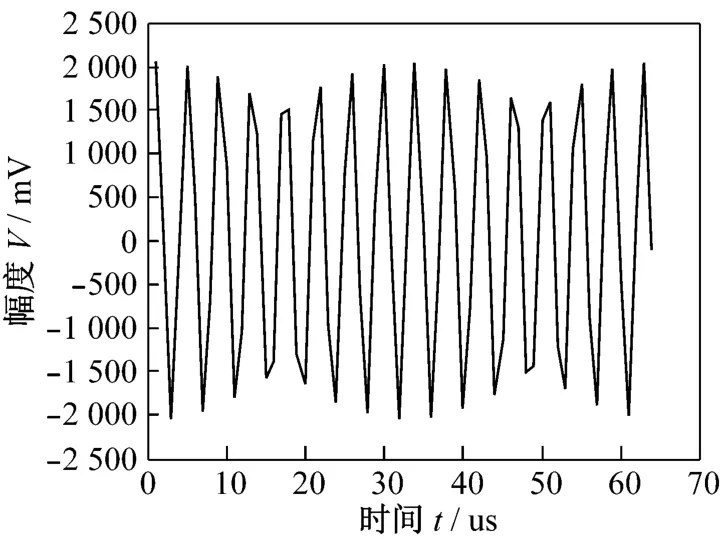
图7 输入信号虚部
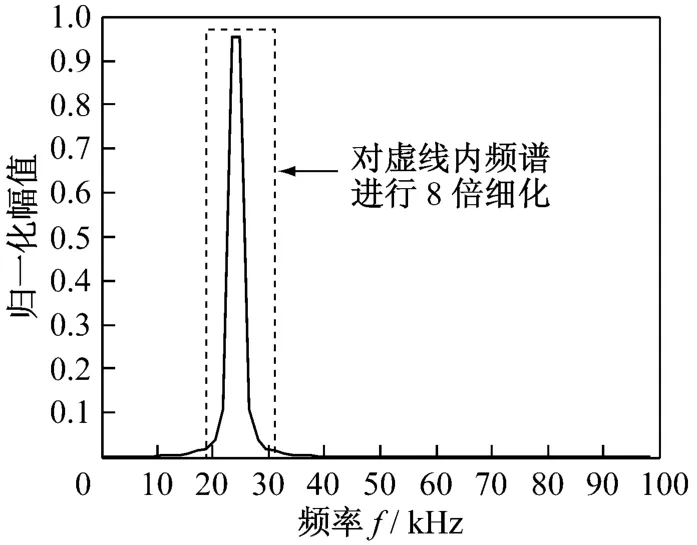
图8 64点FFT计算结果
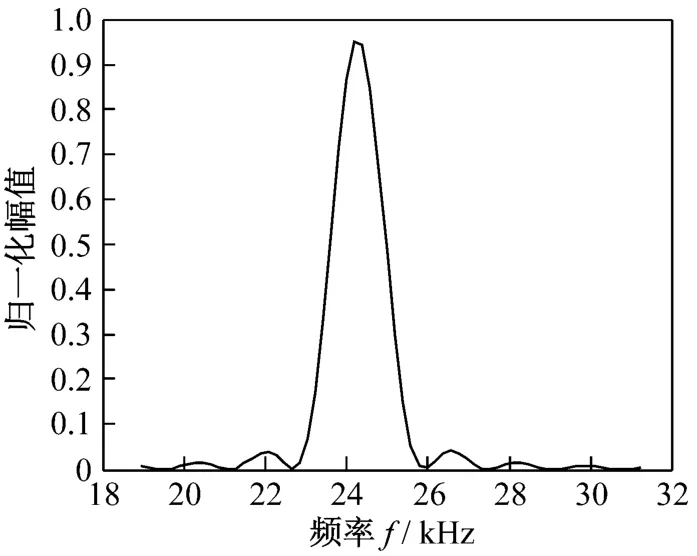
图9 64点8倍细化CZT计算结果
3 结束语
本文根据工程应用的需要,首先阐述了传统使用DSP实现CZT所面对的不足,然后从CZT的原理出发,提出了基于 FPGA硬件平台实现CZT的方法。试验证明该方法的实时性比传统使用DSP实现显著提高,并且易于硬件实现,具有较高的工程应用推广价值。
[1] 项春,董浩,周敏.基于频谱校正理论的全息谱研究[J].煤矿机械,2007,(6):55-58.
[2] 俞宁.CZT-ZDFT算法及实现[J].武汉水利电力学报,2001,4(2):126-136.
[3] 王世一.数字信号处理[M].北京:北京理工大学出版社,1986.
[4] 丁康,张晓飞.频谱校正理论的发展[J].振动工程学报,2003,3(1):14-22.
[5] 魏红亮,李明.一种快速的DBS多普勒中心的估计方法[J].制导与引信,2009,30(1):42-45.
