SAR轨迹偏离条件下三维场景回波模拟研究

任三孩 常文革

(国防科技大学电子科学与工程学院 长沙 410073)

0 引 言

合成孔径雷达(SAR)是一种主动微波遥感成像系统,为了获得高精度的回波数据,国内外都进行了深入的研究,但研究大多都是基于雷达平台匀速直线运动的前提[1],这对于星载SAR来说是个很好的近似,可是对于机载 SAR或弹载SAR来说,由于大气干扰的影响,雷达平台很难作匀速直线运动,其实际轨迹相对于理想轨迹会有一定的偏离[2].SAR的轨迹偏离可以在成像处理阶段通过运动补偿(MOCO)来补偿掉,因此为了更好的验证这些算法的有效性,SAR轨迹偏离条件下的回波模拟研究就很有必要.

对于回波模拟算法,时域法虽然可以精确的模拟出SAR的轨迹偏离,可是太耗时,不实用.因此人们研究了SAR轨迹偏离条件下回波模拟的二维频域法,其中意大利的Giorgio Franceschetti给出了在窄波束和慢轨迹偏离变化条件下的回波模拟方法,此方法相对于理想轨迹的二维频域法没有增加计算时间,可是由于算法对轨迹偏离的严格限制,也限制了其应用范围[3].此后,Giorgio Franceschetti又给出了任意轨迹偏离条件下的回波模拟方法,此方法虽然可以适用于任意的轨迹偏离,但在回波模拟中需要一个积分,增加了计算时间和难度[4].

本文在前面研究的基础上,提出了一种改进的SAR回波模拟的频域算法,大大减少了SAR回波模拟的时间和难度,并且通过基于变尺度傅里叶变换(SCFT)的运动补偿方法得到了成像结果[5],验证了文中所述算法的有效性.

1 回波信号分析

SAR轨迹偏离条件下的几何关系图如图1所示.图中实线表示雷达实际飞行路线;沿X轴方向的虚线为雷达理想飞行路线;H为载机高度.则雷达实际天线相位中心S(x x,y s,zs)与目标T(x,y,z)之间的距离为

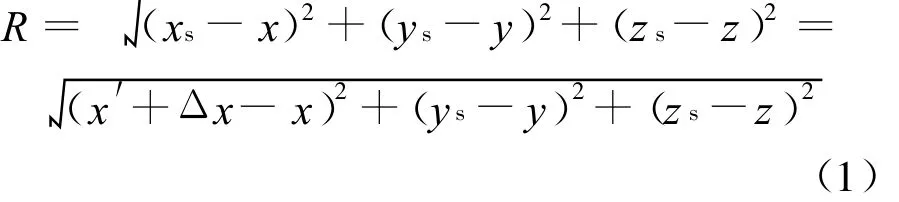
按照上面的分析,式(1)可近似为如下形式

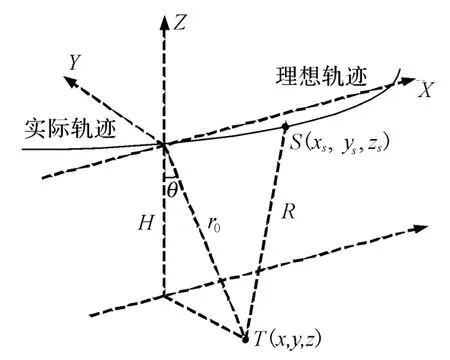
图1 SAR轨迹偏离条件下几何关系图

式中:r0=y2+z2;θ为雷达的下视角.由式(2)可以看出,与理想轨迹相比,轨迹偏离引入了额外的2项,即平台在Y轴和Z轴的位置误差,称为视线方向误差(LOS).

式中:θ=arccos(H/r0),为研究的方便,文中将视线方向误差分解为2部分.

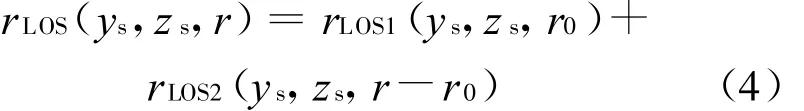
式中:r LOS1为距离向非空变的视线误差;r LOS2为距离向空变视线误差.

假设雷达发射线性调频信号,则接收到的回波在空域可以表示为

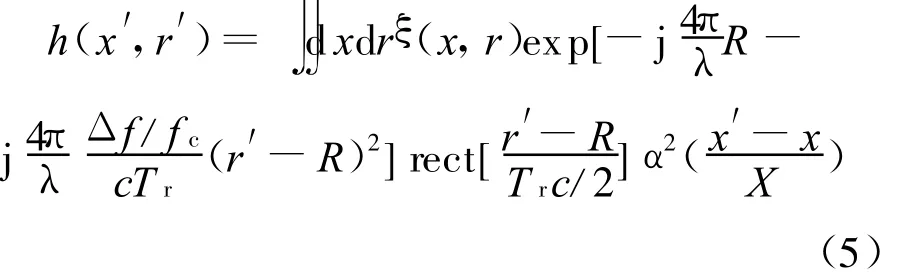
式中:Δf为发射信号带宽;f c为载频;λ为信号波长;Tr为脉冲宽度;c为光速;X为合成孔径长度;(x,r)分别为地面目标在方位向和距离向的位置,(x′,r′)分别为雷达在方位向和距离向的位置.

在中国古代木结构被应用到文化、宗教、住宅等建筑中，另外在大型构筑物与桥梁中也得以应用，木结构的历史漫长，是人类智慧的凝聚，同时也是人与自然的媒介，木结构的发展为我国建筑事业发展注入了生命力。

将回波作距离向的傅里叶变换,得到

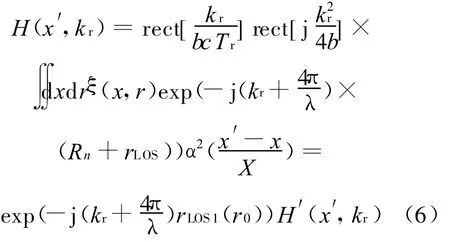
可见,距离向非空变的视线误差可以隔离出来单独处理,为回波模拟提供了方便.下面关键的问题是如何求得(,k r).

将 H′(x′,kr)变换到二维频域,可以得到

式中:G(·)为SAR系统传递函数,且

考虑因子G(kx,kr,r),根据驻定相位原理,可得

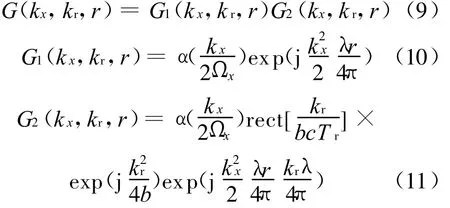
式中:Ωx为方位向带宽,且 Ωx=2π/L,L 为天线方位向尺寸;b=.式(10)中指数项表示方位调制信号,式(11)则描述了距离调制信号和目标的距离迁移(RCM).

注意到式(12)中,目标RCM 因子G2(·)可以从积分式中分离出来.这意味着可以在对空变相位补偿之前进行距离迁移校正(RCMC),空变相位项不影响成像算法RCMC,为运动补偿提供了方便.

将 H″(kx,k r)变换到二维时域

观察积分号里面的表达式,它其实就是在理想轨迹条件下去除距离调制信号和距离单元迁移后的回波表达式,可以按照理想轨迹条件下SAR回波模拟的二维频域法来求解.

2 算法分析

在以上SAR轨迹偏离条件下回波模拟算法分析中,存在两个重要的近似条件,即

2.1 波束角的影响

由式(15)可知,其成立必须满足的条件为

等价于

式中:rmax为轨迹偏离的最大值;Lr天线距离向实际尺寸.其物理意义就是雷达天线在俯仰向的波束宽度足够窄.

以雷达天线在距离向的实际尺寸为20 cm,带宽为200MH z为例,设X波段波长为0.03m,则=0.15,此时rmax≪5 m,很容易满足;设P波段波长为0.75m,此时=3.75,r max ≪0.2m,这个不能满足,即式(18)的近似条件不能成立.

2.2 相对带宽的影响

由算法推导可知,式(16)成立的一个必备条件为

式(19)实际上描述的是雷达距离波数应远小于载波波数.在窄带SAR系统中,由于相对带宽较小,距离波数以载波波数为中心,在一个很小的范围内变动,因此式(19)表示的近似条件成立,而对于大相对带宽则未必.

以X波段窄带SAR和P波段SAR为例,设X波段的中心频率为10 GHz,发射信号带宽为250 MHz,则 kr∈[-0.012 5,0.012 5],式(19)成立;设P波段SAR中心频率为500 MH z,发射信号带宽为 500 MH z,此时 kr∈[-0.25,0.25],显然,式(19)表示的近似条件不成立.

由分析可以得出,文中所提算法适用于SAR轨迹偏离条件下窄带窄波束的回波模拟研究.

3 仿真结果

为验证文中算法的正确性,给出一个根据敦煌某地区实测DEM 数据进行的仿真,见表1.

表1 系统仿真参数

仿真结果如图2所示,其中图2a)为雷达视线误差曲线图,满足文中所述条件.图2b)为根据文中所述算法得到的回波,对其进行成像处理得到如图2c)和图2d)的结果,其中图2c)为未进行运动补偿时的成像结果,可以看出SAR图像在距离向和方位向均有散焦现象;图2d)为根据基于SCFT的一阶和二阶运动补偿算法得到的成像结果,效果比较理想,证明了文中算法的正确性.

在计算机上模拟1 km×1 km的场景,利用文中所述算法只需要4.5 h,而在理想轨迹条件下,运用同样的计算机配置,仿真同样大小的场景需要4 h.因此,文中所述算法相对于理想轨迹没有太大的增加仿真时间.

4 结 束 语

针对SAR轨迹偏离条件下三维场景回波模拟,提出了一种改进的SAR回波模拟频域算法,通过对此模式下回波信号的分析,推导了改进的SAR回波频域模拟公式,并具体说明了SAR轨迹偏离条件下三维场景回波的模拟方法和模拟过程.最后利用实测DEM数据进行了仿真,得到了理想的结果,验证了文中所述算法的正确性,并且仿真时间相对于理想轨迹没有太大的增加.

由文中分析可知,所提算法适用于SAR轨迹偏离条件下窄带窄波束的回波模拟,因此SAR轨迹偏离条件下大相对带宽、大波束角的SAR回波模拟是下步研究的重点.

图2 仿真结果

[1]任三孩,常文革,李建阳.具有地面起伏特征的三维场景回波模拟研究[J].雷达科学与技术,2007,5(5):342-348.

[2] 保 铮,邢孟道,王 彤.雷达成像技术[M].北京:电子工业出版社,2005.

[3]FranceschettiG,Iodice A,Perna S,etal.SAR sensor trajectory deviations:fourier domain formu lation and ex tended scene simu lation of raw signal[J],IEEE Trans.Geosci.Remote Sensing,2006,44(9):2323-2333.

[4] Franceschetti G,Iodice A,Perna S,et al.Efficient simulation of airborne SAR raw data of extended scenes[J],IEEE Trans.Geosci.Remote Sensing,2006,44(10):2851-2860.

[5]郑卫平,张秋玲,冯宏川,等.基于SCFT处理算法的机载SAR运动补偿[J],电子与信息学报,2005,27(9):1375-1378.