超高速注塑机电液系统的分析与仿真研究
2010-11-29蔡康雄文生平温展飞
蔡康雄,文生平,温展飞,金 晖
(1.华南理工大学聚合物成型加工工程教育部重点实验室,广东广州510640;2.贝加莱工业自动化(上海)有限公司广州分公司,广东广州513630)
超高速注塑机电液系统的分析与仿真研究
蔡康雄1,文生平1,温展飞1,金 晖2
(1.华南理工大学聚合物成型加工工程教育部重点实验室,广东广州510640;2.贝加莱工业自动化(上海)有限公司广州分公司,广东广州513630)
通过分析超高速注射液压系统中的比例压力阀、比例流量阀、蓄能器和液压缸的物理结构,建立了注射系统的理论数学模型,搭建了MATLAB模型并对其进行系统仿真。通过系统的动态特性找到了控制超高速注射速度的关键因素。仿真结果表明,注射系统对注射速度的响应时间要求比较严格时可采用控制伺服阀的方式;注射系统对注射速度的幅值要求比较严的可采用控制比例方向阀的方式。
超高速;注塑机;电液系统;仿真
0 前言
注射成型是规模化、自动化,机械化加工塑料产品的重要方法。进入21世纪后,IT行业的小型化,产品的多样化、精密化成为发展趋势,要求注射成型向着高精度、高重复性、节能、高效、超高速、省空间及环保等方向发展[1]。超高速注射速度具有以下优点:(1)极高的剪切速度使得塑料的黏度下降,在低黏度的情况下容易实现超薄成型以及减少制品的扭曲和翘曲变形[2];(2)减少表面的流纹与熔接线,提高制品的表面光泽,提高熔接部位强度,防止冷却变形[3];(3)缩短了注射周期,提高注射效率和节能效果。因此,超高速注射速度受到国内外注塑机厂商的追捧,日本注友机械有限公司推出多款注射速度高达4000 mm/s的液压注塑机。
超高速注射速度的实现有如下几个困难:(1)要保证在注射过程中液压系统能够提供足够的液压能;(2)要解决注射过程中引起的震动、冲击等问题。Tsai[4]、Wang[5]、Yu[6]等指出,超高速液压注塑机采用超高速响应和高精确的大容量的蓄能器以及快速响应的伺服、比例阀后能够达到超高速注射速度要求;在减速阀前加一个小蓄能器能够有效地减少震动和冲击。该方法已经在工业中应用,例如Ine Well Machinery公司的SW-HSB系列、Sumitomo公司的SE-HY系列、BMC公司的FT-260BMC型号等。根据上述方法研制成的注塑机液压系统示意图如图1所示。

图1 液压系统示意图Fig.1 Diagram of the hydraulic system of the injection molding machine
为得到关于注射速度的系统数学模型,本文首先对液压系统进行如下假设:(1)速度调节过程中液压系统的系统压力不发生改变;(2)液压管道的油介质阻尼和泄露忽略不计;(3)在速度调节过程中只考虑缓冲蓄能器。
1 数学模型
1.1 比例方向阀的数学模型
比例方向阀的内部结构较复杂。为了研究方便,忽略比例方向阀结构中的一些次要因素,得到的比例方向阀的结构图示意图如图2所示[7]。

图2 比例方向阀结构示意图Fig.2 The schematic diagram of proportional direction valve
比例方向阀中的电感和电容阻抗值较小,可以忽略不计,只考虑其中的电阻因素后,电磁铁对滑块的电磁吸力(Fmv)与输入电压值(u)的关系式为:

比例方向阀阀芯的动量方程为:

式中 f——摩擦力,N
mv——阀芯质量总和,kg
Bi——黏滞阻尼系数,N·s/m
kv——阀的弹性刚度,N/m
av——阀芯加速度,m/s2
vv——阀芯的速度,m/s
kuv——比例系数
xv——阀芯位移,m利用式(1)和(2)得到比例方向阀的MA TLAB/SIMULIN K仿真子系统图,如图3所示。

图3 比例方向阀的MATLAB/SIMULINK子系统Fig.3 The subsystem of MATLAB/SIMULINK ofproportional direction valve
比例方向阀的流量方程为:

式中 Q1——比例方向阀入口流量,m3/s
k——比例方向阀的流量系数,m4/s
w——比例方向阀的相对面积梯度
P——比例方向阀入口液压压力,N
Q5——比例方向阀回油流量,m3/s
P3——比例方向阀回油液压压力,N
P1——液压缸注射液压压力,N
ρ——流体密度,kg/m3
1.2 伺服节流阀的数学模型
一级比例伺服节流阀的流量比较小,这里采用二级喷嘴伺服阀。为研究方便,忽略伺服阀结构中的反馈和其他一些次要因素后,伺服阀的物理结构如图4所示。

图4 喷嘴伺服阀物理结构示意图Fig.4 The structure of the servo valve
同理在只考虑电阻的情况下,喷嘴所受的力Fs与输入电信号us成正比关系:

伺服阀喷嘴处的动量方程为:

式中 Ms1——伺服阀喷嘴结构的当量质量,kg
r——喷嘴的受力半径,m
θ——喷嘴向左旋转的角度,rad
fs1——喷嘴旋转的阻尼,可以忽略不计,N·m
Bs1——伺服阀喷嘴结构的黏滞阻尼系数,N·s/m
ks1——伺服阀喷嘴结构的弹性刚度,N/m
喷嘴导管的流量方程为:

式中 q1——导管左边的流量,m3/s
q2——导管右边的流量,m3/s
Vs1——导管右边的体积(加上二级阀的驱动腔的体积),m3
Vs2——导管左边的体积(加上二级阀的驱动腔的体积),m3
kθ——喷嘴处的流量比例系数,m3/s
α——喷嘴处比例常数
p1——导管左边的压力,N
p2——导管右边的压力,N
Cip——液压缸内泄露系数,m4·s/kg其中由于阀芯的运动量较小,所以把Vs1与Vs2看成近似相等。对式(7)~(10)进行处理后得:

式中 pl——喷嘴的驱动负载,pl=p2-p3
βe——液压油的弹性模量,kg·m/s2
伺服阀二级阀的动量方程为:

式中 A——二级阀的阀芯面积,m2
Ms2——二级阀的当量质量,kg
xs——二级阀阀芯的位移,m
fs2——二级阀阻尼系数,可以忽略不计,N·m
Bs2——二级阀的黏滞阻尼系数,N·s/m
ks2——二级阀喷嘴结构的弹性刚度,kg·m2/s2
利用式(5)、(6)、(11)和(12),得到伺服阀的MATLAB/SIMULIN K仿真子系统图,如图5所示。
比例伺服节流阀的流量方程为:
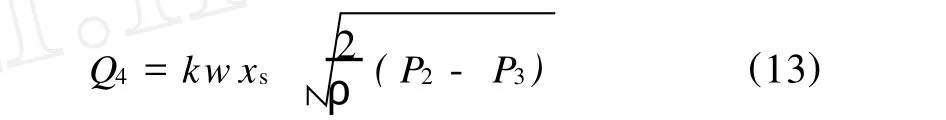
式中 Q4——伺服阀回油流量,m3/s
P2——伺服阀进油腔的液压压力,N
1.3 缓冲蓄能器的数学模型
超高速注塑机在注射速度改变的瞬间,由于液压缸的活塞的惯性作用,会对整个液压系统产生很大的冲击。缓冲蓄能器安装在伺服阀的前面,能够有效地减少液压引起的震动和冲击。

图5 伺服阀的MATLAB/SIMULINK子系统Fig.5 The subsystem of MATLAB/SIMULINKof the servo valve
蓄能器吸收和释放液压油的过程中,只需考虑P2和蓄能器内气体的压力(Pa)之间的力学平衡关系和蓄能器内气体的绝热过程[8]。
液压油压力P2和Pa之间的力平衡方程为:

式中 Aa——蓄能器的内环面积,m2
Ab——油管的内环面积,m2蓄能器内气体的绝热过程为:

式中 C——常数
对式(14)和(15)在(Pa,Va)进行求导处理并略去高次项,得:

把式(16)和(19)代入式(18)式后,得:

式中 n——气体状态系数,n=1.4
Q3——蓄能器流出或者流入的液压流量,m3/s
Va——蓄能器在注射速度刚开始改变时的气体
容量,m3
1.4 注射液压缸的数学模型
注射液压缸是此系统的执行机构。忽略液压缸结构中的次要因素,得到注射液压缸的结构示意图,如图6所示。

图6 液压缸的结构示意图Fig.6 The structure of hydraulic cylinder
考虑液体的可压缩性,密闭容腔有流量进出,容积变化以及有压力作用时,液压缸前后腔的流量连续性方程为[9]:

式中 Q1——液压缸进油流量,m3/s
Cep——液压缸外泄露系数,m4·s/kg
V1——液压缸进油端的体积,m3
V2——液压缸出油端体积,m3
βe——液压油的弹性模量,kg/(m·s2)
液压管道中伺服阀与注射油缸、蓄能器之间,比例方向阀与伺服阀之间的流量关系为:

把式(4)和(13)代入式(24)得:

对其进行整理后有:

而对于液压缸两端的液压压力和活塞的力平衡方程:

式中 M——活塞的当量质量,kg
By——活塞的黏滞阻尼系数,N·s/m
KS——活塞的当量弹性刚度,kg·m2/s2
PL——注射当量负载压力,N·m
Ae——活塞负载端当量面积,m2
对式(13),(20),(23),(26),(22)进行处理,消去Q2、Q3、Q4和P3,得到:

把式(3)、(21)进行处理,得:

根据式(27)、(28)和(29)得到液压缸的MATLAB/SIMULIN K子系统结构图,如图7所示。
2 系统仿真
仿真系统中的系统参数参照实际的产品尺寸和液压系统进行设定。根据伺服阀和比例方向阀产品的技术参考资料,可以得到阀芯的质量mv=0.4 kg和刚度系数ks=20000N/m,kv=20000N/m,Bs1=100 N·s/m,Bs2=115 N·s/m,Bi=250 N·s/m。
根据液压缸和蓄能器的工况,得到A1=179.1 cm2,
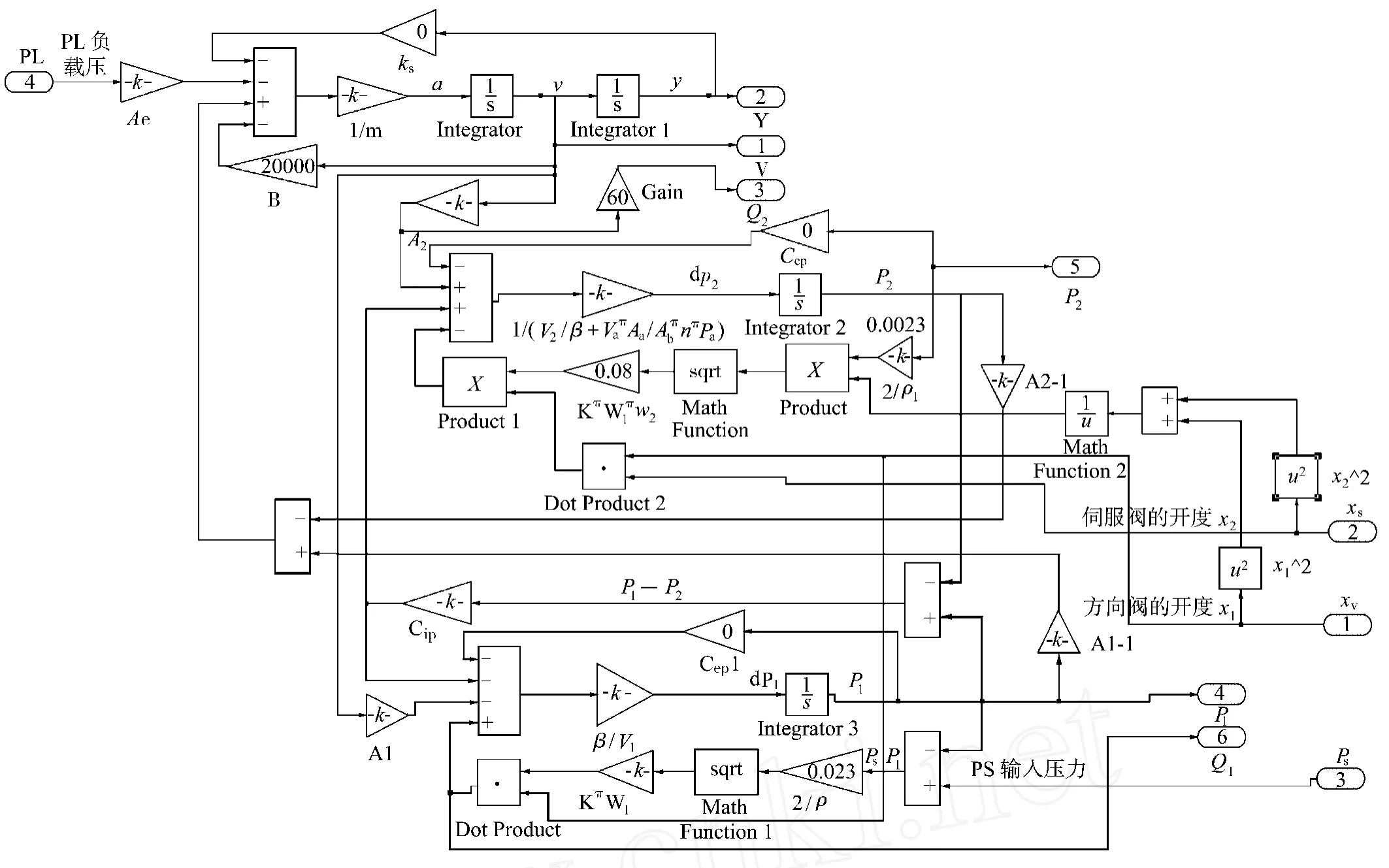
图7 液压缸的MATLAB/SIMULINK子系统结构图Fig.7 The subsystem of MATLAB/SIMULINKof the hydraulic cylinder
A2=81.5 cm2,M=75 kg,Ae=49.6 cm2,βe=1.2×109kg/(m·s2),Cip=4.5×10-11m4·s/kg,Cep的大小可以忽略不计。
根据注射系统各个组成部分的数学关系,把系统开环模型看成是双输入双输出的模型。为了分析系统中对注射速度控制的关键因素,把系统开环模型分成注射速度关于伺服阀的系统模型和注射速度关于比例方向阀的系统模型,如图8所示。
在空载情况下,把两个一阶响应都设定为初始值2,终值10后系统的开环响应曲线如图9所示。
从系统的开环响应曲线可以得到:(1)注射速度关于伺服阀的静态响应时间比较短,只有100 ms左右,注射速度关于比例方向阀的静态响应时间在300 ms左右;(2)比例方向阀对注射速度的影响较小,伺服阀是注射速度控制的关键因素;(3)两个系统都具有稳定的静态特性。


图8 系统的MATLAB模型Fig.8 MATLAB model of the system

图9 仿真曲线Fig.9 The simulation diagram
3 结论
(1)注射系统对注射速度的响应时间要求较严格时,可以采用控制伺服阀的方式;
(2)注射系统对注射速度的幅值要求较严时,可以采用控制比例方向阀的方式。
[1] 谢鹏程,丁玉梅,杨卫民.前端控制式新型超高速精密注射成型原理的研究[J].中国塑料,2005,19(10):60-63.
[2] 李红林.超高速注射成型及模具技术[J].新技术新工艺,2005,(3):44-45.
[3] 吴智华.注射成型技术的发展动态[J].塑料包装,2001,11(4):15-26.
[4] Ching Chih Tsai.Mechatronic Design and Injection Speed Control of an Ultra High-speed Plastic Injection Molding Machine[J].Mechatronics,2009,19:147-155.
[5] Wang Y S.The Investigation of Hydraulic Servo System Design forHigh-speed/Injection Molding[D].Jhongli:Mechanical Engineering Research Institute,Chung Yuan University,2001.
[6] Yu C Y.A Study on the Regulating Response Characteristics of Hydraulic Servo System for the High-speed Injection Molding[D].Jhongli:Department ofMechanical Engineering,Chung Yuan University,2002.
[7] 杨 俭.电液比例位置系统复合控制及相关研究[D].杭州:浙江大学机械学院,2005.
[8] 邵安岑.电液比例压力流量复合控制阀的特性研究[D].杭州:浙江大学机械学院,2002.
[9] 刘成峰.注塑机电液控制系统的建模及仿真研究[D].太原:太原理工大学机械学院,2003.
Analysis and Simulation of Electro-hydraulic Systems of Ultra High Speed Injection Molding Machines
CAI Kangxiong1,WEN Shengping1,WEN Zhanfei1,J IN Hui2
(1.The Key Laboratory of Polymer Processing Engineering,Ministry of Education,South China University of Technology,Guangzhou 510640,China;2.Guangzhou Branch of Bernecker&Rainer Industrial Automation(Shanghai)Co,Ltd,Guangzhou 513630,China)
The mathematical models of ultra high speed injection systems were formulated through the analysis of the physical structure of the proportion delivery valve,the proportion flow valve,the accumulator and the hydraulic carries.In addition,the dynamic characteristic of the system was simulated using MATLAB.The key factor controlling the speed was found based on the system′s dynamic characteristic.It showed that when the response time of the injection system to the injection velocity was strict,controlling serve valves should be used;when the response amplitude of that was strict,controlling proportional directional valves should be used.
ultra high speed;injection molding machine;electro-hydraulic system;simulation
TQ320.66+2
B
1001-9278(2010)02-0103-06
2009-09-16
联系人,caikangxiong@163.com
