用BP神经网络提高锂离子电池化成系统采样精度
2010-11-29吴免利李劼肖昕邹忠
吴免利,李劼,肖昕,邹忠
(1. 中南大学 冶金科学与工程学院,湖南 长沙,410083;2. 中南大学 信息科学与工程学院,湖南 长沙,410083)
在电池化成过程中,对充放电电压和电流的要求都非常严格,过充电会造成锂离子在负极堆积形成枝晶,刺穿隔膜,形成内部短路,对电池的内部材料造成不可逆影响,降低电池使用寿命,严重时会造成电池热失控而爆炸,对生产造成很大的损害[1−5]。不准确的电流和电压不利于锂离子动力电池的分选和配组,使得配组后的单体电池差异性较大,严重缩短电池组的使用寿命[6]。湖南中大业翔公司自行研制的YX-20A型锂离子动力电池化成检测设备,由于使用较多的非线性元件使得采样信号和实际的测量值之间存在较大误差。如果单从硬件上改进,会增加硬件成本,因此,研究一种合适的方法对数据进行修正,来提高系统采样精度是非常必需的。经实验证实,用普通的线性回归模型校正采样数据,对提高电压采样精度有较好的效果,但对提高电流精度效果不佳。人工神经网络(Artificial neural network, ANN)算法可以在对被测对象不完整或不确定认识的基础上表示任意非线性关系,因此,为解决上述采样数据失真问题提供了一种思路。目前神经网络模型多达几十种,其中,最典型的就是 BP神经网络。此网络具有结构简单、训练算法理论依据可靠、推导严谨且易于实现、预测能力强等特点[7−10]。为了提高系统充放电控制和采样精度,本文作者利用 BP神经网络对非线性系统的学习能力校正系统误差,并提高控制精度。
1 误差分析
YX-20A型锂离子动力电池化成系统的电源控制采用脉冲宽度调制(PWM)的调制方式,在主控器向电源控制板传输电压电流基准后,控制板上的PWM控制芯片TL494将根据采样的电池电压或电流控制功率板上 MOS管的开关,从而调节充放电电流。功率板的电路图如图1所示,包括MOS管控制电路和检测回路。
图1中的MOS管、电感、电容和TL494一起组成PWM电源调节电路,通过调节TL494的占空比调节回路中的电压和电流。但这些器件都属于非线性元件,经调节后回路中电池的电压和电流与设定基准存在一定的偏差,同时,由于化成柜在充放电阶段会将大量电能以电阻发热形式释放,因此,作为电流检测的康铜丝电阻,在较高的温度下也存在一定的非线性特征,造成采集数据失真。PWM 调节电路工作时产生的高频脉冲也对系统的精度产生较大的影响。
在数据采样上,电压误差都在1.5%左右波动,用普通的线性回归模型校正采样电压可以取得理想的效果。而电流的误差大于 5%,且波动较大,用同样的线性方法对采样电流进行校正,效果并不佳。电流采样误差过大会降低 TL494芯片调节的精度,在 10~40 ℃的测试结果表明:PWM转换过程中电流最大相对误差为 24%,平均相对误差约为6.4%。
2 模型建立和数据处理
2.1 BP神经网络模型的建立
BP网络是通过将网络输出误差反馈回传对网络参数进行修正,从而实现网络的映射。具有1个隐含层的三层 BP网络可以有效地逼近任意连续函数。考虑到实际应用的要求,网络设计时尽可能地减小系统的规模和复杂性,同时考虑到设备周围环境温度对硬件性能的影响,本文作者采用2-q-1 型三层BP网络,即具有2个节点的输入层、具有q个节点的隐含层和具有1个节点的输出层。输入层分别输入A/D转换后的电流和环境温度;输出层为校正后的电流,隐含层的节点个数q通过实验的方法确定。
传统的 BP神经网络是一种简单的最速下降静态寻优方法,在修正权值和阈值时,只按照当前的负梯度方向进行修正,而没有考虑到以前积累的经验,即以前时刻的梯度方向,从而使学习过程发生振荡,收敛缓慢。因此,采用常用的改进算法——动量梯度下降法和L-M(Levenberg-Marquardt)算法对BP神经网络进行对比训练。

图1 功率板电路图Fig.1 Circuit diagram of power board
动量梯度下降法的具体做法是:将上一次权值和阈值调整量的一部分迭加到按本次误差计算所得的权值和阈值调整量上,作为本次的实际权值和阈值调整量,即
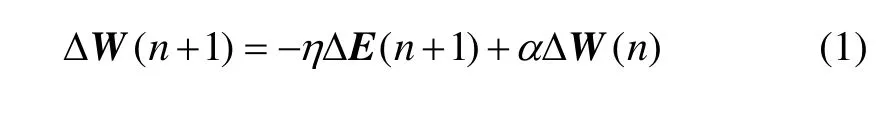
其中:α为动量系数;η为学习率。
对于第p个样本,在本模型中L-M算法的权值和阈值调整量为:
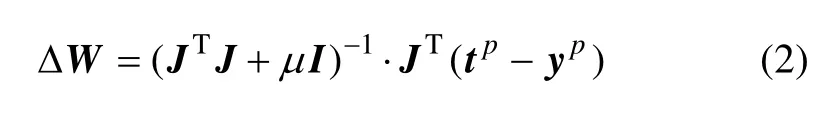
其中:J为网络误差对权值和阈值导数的Jacobian矩阵;µ为比例系数,tp为期望输出;yp为输出向量。
隐含层中的激励函数取Sigmoid函数,即

输出层中的激励函数取线性函数,即

对于隐含层节点的选取,有如下经验公式:
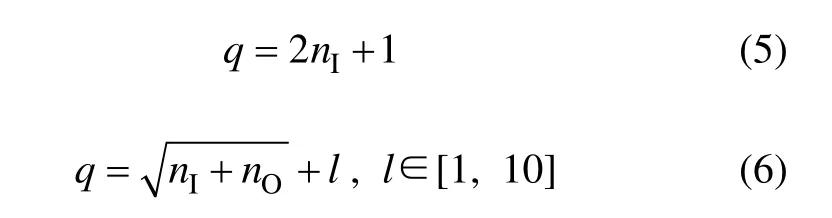
其中:nI为输入层节点数;nO为输出层节点数;q为隐含层节点数。
根据这2个经验公式确定q的取值范围,然后,通过实验对比确定合适的q。选取q为3~11范围内的9个节点进行对比实验来确实理想的q。训练时设定最大训练步数为10万步,误差精度为0.000 1。
2.2 样本的选择
在不同的环境温度下,上位机对设备设定由低到高的不同电流基准,当系统运行时,在回路上测量通过电池的实际电流,同时记录当前的A/D转换值。将环境温度和不同设定基准测得的A/D转换值作为神经网络的输入;将回路上实际测量得到的电流转换到与A/D采样值相同的度量模式下,作为神经网络系统的输出对神经网络进行训练。
化成柜的工作状态有恒流充电、恒流放电、恒压充电、搁置和循环5类,其中:循环是前4种工步的组合;在搁置状态下,充放回路是断开的,电路中只有细小的电流。对恒流充电、恒流放电、恒压充电分开进行训练。本文仅以恒流充电为例进行说明。电池化成车间的工作温度一般为10~40 ℃,锂离子动力电池的恒流充电阶段电流一般为1~10 A。所以,在10~40 ℃(温度误差为±1 ℃)选取1~10 A的点进行训练,积累典型样本,表1所示为1个典型样本在不同温度下的电流。
训练数据的相对误差如图2所示。由图2可以看出:在不同温度下,电流的A/D转换值与真实值的误差波动都较大,最大波动幅度可达 5%,并且规律性不确定,表明训练数据的非线性特征明显。

表1 恒流充电过程中典型样本的电流Table 1 Current of typical sample during constant-current charging process 电流/A
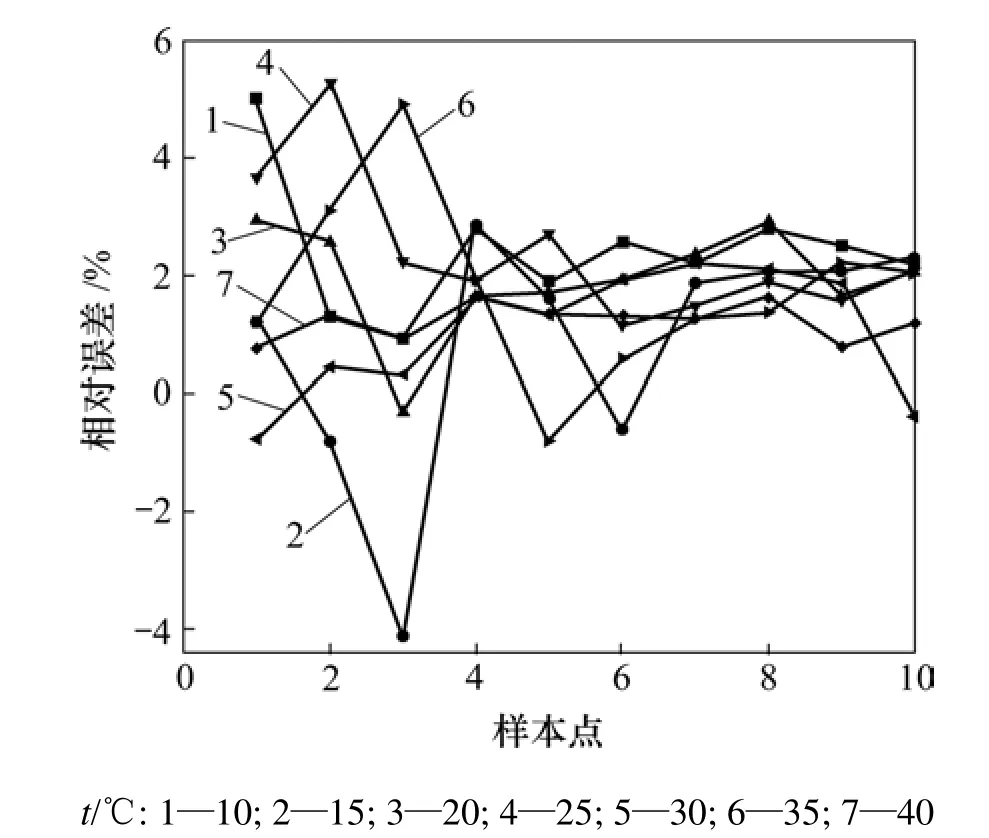
图2 电流相对误差Fig.2 Relative errors of electric current
2.3 样本的预处理
训练之前,为了保证训练的准确性,消除其他因素的影响,需对数据进行归一化。归一化公式为:

其中:xmax和 xmin分别为每个输入向量的最大值和最小值。
加入修正数值0.95和0.05的目的是使样本电流落在[0.05, 0.95]这个区间,避免数据中出现0和1,使网络具有较好的性能。
3 结果分析
3.1 BP网络训练及模型参数优化
用不同隐含层节点数及算法对积累的典型样本进行训练,并将训练好的神经网络对电路中的电流测量值进行预测,并与实际电流进行比对,得到电流最大相对误差及平均相对误差,结果如表2所示。表2中电流均为每项实验过程中偏差的最大电流。
从表2可知:当采用动量梯度下降法时,网络不能收敛到设定误差精度的隐含层节点数分别为 3,4和11;当节点数不为3,4和11时,都可以收敛到设定误差精度,但是训练步数全部在1万步以上,在此优化算法下,隐含层节点的个数为6时效果最好,最大误差为 2.53%,平均误差为 0.92%,训练步数为106 822;而采用L-M算法,网络不能收敛于设定误差精度的隐含层节点数都不大于 5,当节点数大于 5时,都可以很快收敛到设定误差精度,并且训练步数全部在400以下,当隐含层节点数为9时,最大误差为0.90%,平均误差为0.33%,训练步数为18。通过上述对比可知,采用隐含层节点数为9的L-M算法,其训练的收敛速度比采用动量梯度下降法要快很多,并且校正的精度比采用动量梯度下降法的收敛速度校正的精度高。
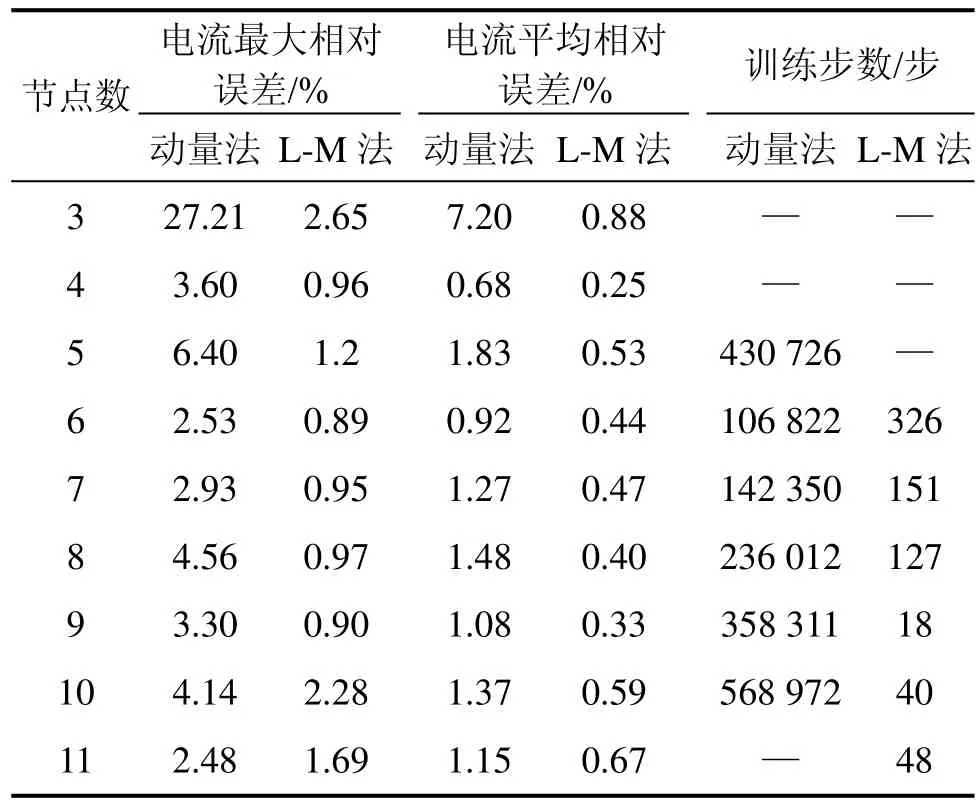
表2 电流的预测结果Table 2 Prediction results of electric current
3.2 设定基准值对应的相对误差校正结果
采用上述恒流充电过程中得到的L-M BP神经网络,对采样电流进行校正,然后,根据校正后的A/D转换值,通过TL494芯片调节系统回路中的电流,使之接近电流的设定基准。测得基准电流和实测值之间的相对误差曲线如图3所示。
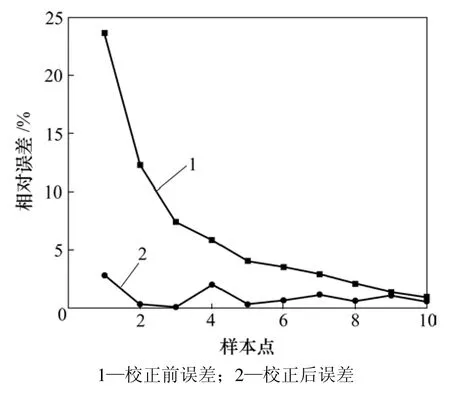
图3 基准电流和实测值之间的相对误差Fig.3 Relative errors between measured currents and basic set-point currents
由图3可知:在恒流充电过程中,校正前基准电流和实测值之间的相对误差随着电流的增大而减小,校正后基准电流和实测值之间的相对误差波动较为平缓;基准电流和实测值之间的最大相对误差由校正前的24%左右下降为校正后的3.5%左右;平均相对误差由校正前的 6.4%左右减小到校正后的 1.2%左右。可以看出:基准电流和实测值之间的最大相对误差比校正前明显下降;平均相对误差的下降也很显著。
采用相同的网络模型,在恒压充电、恒流放电过程中,得到电流基准值与实测值间的最大相对误差小于 1.1%,平均误差为 0.5%左右。表明校正后设定基准和实测值的误差也得到了较好控制。
4 结论
(1) 隐含层节点数为9的L-M BP神经网络算法对工业采样的样本能较快收敛,并且校正效果明显比采用动量梯度下降法的BP神经网络的校正效果好。
(2) 在恒流充电过程中,用L-M BP神经网络算法能将电流的误差控制在 0.9%以内;采用通过校正的A/D转换值调整实际电流,校正后基准和实测值最大误差在3.5%左右,表明此方法能在一定程度上提高系统精度。
(3) 对于神经网络算法,训练样本的选择对降低训练成本和提高网络泛化能力有较大的影响。训练样本除了数量要足够多外,还应涵盖各种可能出现的样本类型,以满足各种样本组合和拟合精度要求。本文没有考虑样本的选择对网络泛化能力的影响,同时也没有考虑设备的老化等可能导致影响精度的问题,所以,神经网络算法能否真正可靠地应用在对稳定性要求很高的工业生产设备上还有待进一步验证。
[1]ZENG Yu-qun, WU Kai, WANG De-yu, et al. Overcharge investigation of lithium ion polymer batteries[J]. Journal of Power Sources, 2006, 160(2): 1302−1307.
[2]庞静, 卢世刚, 刘莎. 锂离子电池过充特性的研究[J]. 电化学,2005, 11(4): 398−401.PANG Jing, LU Shi-gang, LIU Sha. A study of overcharge characteristic of lithium-ion cells[J]. Electrochemistry, 2005,11(4): 398−401.
[3]周震涛,覃迎峰. 锂离子电池过充电行为研究[J]. 电池, 2004,34(5): 326−327.ZHOU Zhen-tao, QIN Ying-feng. A study of the overcharge behavior of Li-ion batteries[J]. Battery, 2004, 34(5): 326−327.
[4]王震坡, 孙逢春, 林程. 不一致性对动力电池组使用寿命影响的分析[J]. 北京理工大学报, 2006, 26(7): 578−580.WANG Zhen-po, SUN Feng-chun, LIN Chen. An analysis on the influence of inconsistencies upon the service life of power battery packs[J]. Transactions of Beijing Institute of Technology,2006, 26(7): 578−580
[5]陈松林, 李革臣, 武云丽. BP神经网络在电池分选中的应用[J]. 哈尔滨理工大学学报, 2001,6(5): 10−13.CHEN Song-lin, LI Ge-chen, WU Yun-li. The application of BP neural network in battery-sorting[J]. Journal of Harbin University of Science and Technology, 2001, 6(5): 10−13.
[6]凌国维, 唐致远, 王琪. 人工神经网络在锂离子动力电池管理中的应用[J]. 电源技术, 2006, 130(10): 849−851.LING Guo-wei, TANG Zhi-yuan, WANG Qi. Utilization of artificial neural networks in Li-ion power batteries management[J]. Chinese Journal of Power Source, 2006, 130(10):849−851.
[7]周继成, 周青山, 韩飘扬. 人工神经网络[M]. 北京: 科学普及出版社, 1992: 47−56.ZHOU Jin-cheng, ZHOU Qing-shan, HAN Piao-yang. Artificial neural network[M]. Beijing: Popular Science Press, 1992:47−56.
[8]史春朝. BP神经网络算法的改进及其在PID控制中的应用研究[D]. 天津: 天津大学电气与自动化工程学院, 2006: 41−54.SHI Chun-zhao. Study on algorithm improvement of BP neural networks and its application in PID control[D]. Tianjin: School of Electrical and Automation Engineering, Tianjin University,2006: 41−54.
[9]An G. The effect of adding noise during back-propagation training on a generalization performance[J]. Neural Computation,1996, 8(3): 643−671.
[10]何发祥, 黄英. 用BP网络求解土体的导热系数[J]. 岩土力学,2000, 21(1): 84−87.HE Fa-xiang, HUANG Ying. Solution of thermal conduction coefficient from BP network[J]. Rock and Soil Mechanics, 2000,21(1): 84−87.
