Fe{O(CH2CO2)2}(H2O)2(NO3)电子结构和磁性的第一性原理研究

朱占武 ，揭泉林

（1.武汉大学 物理科学与技术学院，湖北武汉430074；2.湖北汽车工业学院 理学系，湖北十堰442002）

为了设计新的磁性材料，人们开始广泛的关注含有金属离子的分子基永磁材料[1-3]。关于这类材料的一些新的量子现象，例如量子隧道磁化，将来可能会应用于量子计算和数据存储上；还有其他的一些有意义的研究方向比如自旋态过渡、调整磁耦合和设计铁磁体等。这些都能引起从事物理和化学跨学科研究的实验和理论工作者的极大兴趣[4-5]。另外这些材料还可能会具有2个或2个以上的物理特性，使得同一物质兼具磁学和光学性质，从而产生一些新的物理现象和新的应用。与金属相比，有机无机导电体重量轻，延展性好，在电池电极、腐蚀保护和微波屏蔽方面具有巨大的应用潜力[6-7]。而且这类材料的转变温度通常要高于纯自由基有机磁性材料。

金属有机配合物分子磁体是目前研究得最广泛、最深入的一类分子磁体，其自旋载体为过渡金属。在其构建单元中，可以形成单核、双核及多核配合物。由这些配位物进行适当的分子组装，可以形成一维、二维及三维分子磁体，可以形成链状或层状结构.根据桥联配位体的不同，这类分子磁体主要包括草胺酸类、草酞胺类、草酸根类、二肪类、氰根类等几种类型。Fe{O（CH2CO2）2}（H2O）2（NO3）就是典型的以过渡金属铁为顺磁中心的金属有机配合物。本文试图从第一性原理出发来研究该化合物的磁性机制。

第一性原理方法在材料的模拟方面有着广泛的应用，它基于密度泛函理论，不受实验影响，不做过多的假设，从最基础的物理定律出发，对材料作物理特性的探究。因此，采用密度泛函理论（DFT）和广义梯度近似（GGA）计算和研究化合物Fe{O（CH2CO2）2}（H2O）2（NO3）的电子结构和磁性质。为了更好的理解原子间的相互作用，还画出差分电荷密度图并计算了分子磁矩及能带结构和态密度。

1 计算细节

化合物Fe{O（CH2CO2）2}（H2O）2（NO3）属正交晶系，空间群为Aba2。晶格参数a为9.2473A˚，b为10.3115A˚，c为9.3771A˚[8]。通过 X 射线晶体学的研究，化合物Fe{O（CH2CO2）2}（H2O）2（NO3）的分子结构和晶体结构如图1所示[8]。该化合物分子以铁离子为中心，与周围的7个氧原子组成五边形双锥，铁离子周围1个的三齿的oda2-基团和1个双齿NO3-1基团构成主平面，2个水分子分布在轴向。每个晶胞包含有4个 Fe{O（CH2CO2）2}（H2O）2（NO3）分子。

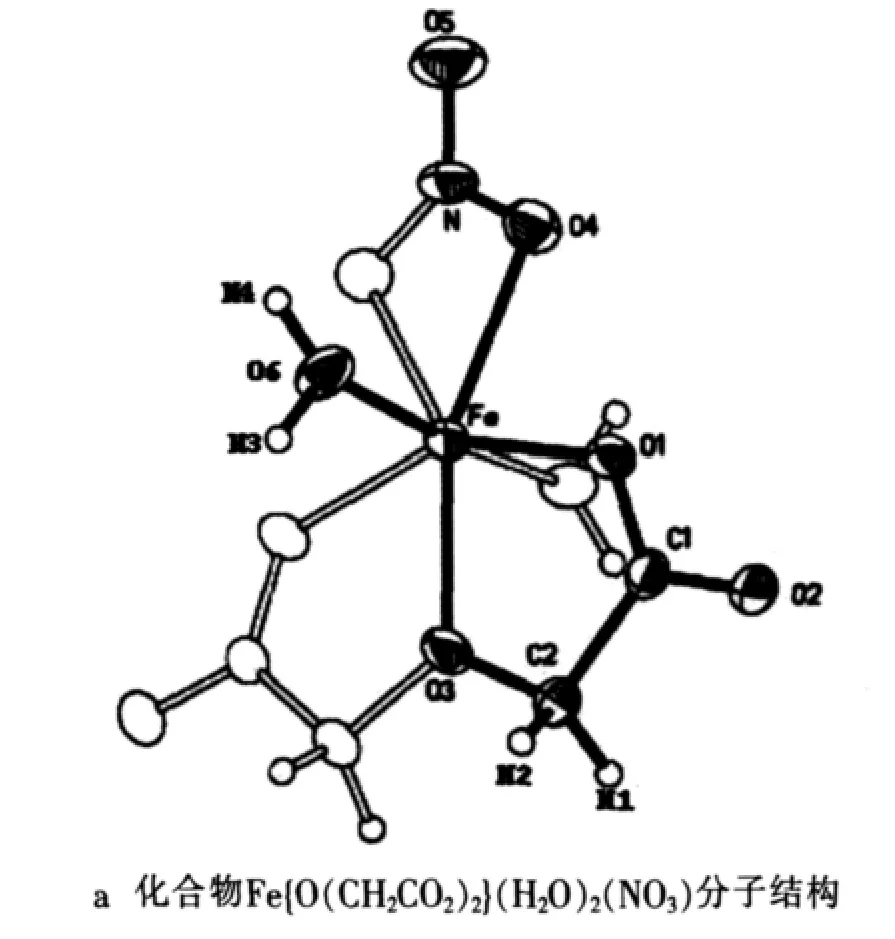
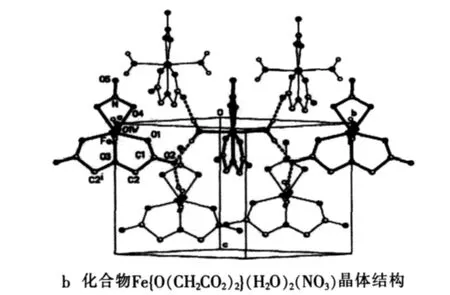
图1 化合物的分子结构和晶体结构

本文所有的计算都是由Vasp（Vienna Abinitio Simulation Package）[9]程序软件包完成的。Vasp软件包是一个基于密度泛函理论的计算程序，赝势采用PAW[10]方法，电子和电子之间的交换关联能采用广义梯度近似（GGA）方法来处理，全布里渊区的求和采用15×15×11的Monkhorst Package型的k点网格，平面波截断能取350eV。测试计算表明，进一步增加平面波截断能量和k点数目对计算结果的影响可以忽略。当系统总能量的变化稳定在10-5eV内时，电子结构的自洽场（SCF）计算停止并认为达到收敛。

2 结果讨论

分别计算了Fe{O（CH2CO2）2}（H2O）2（NO3）铁磁态（FM）和反铁磁态（AFM）态总能量，结果表明，反铁磁态总能量为-263.68502eV，而铁磁态总能量为-263.68419eV。很明显，处于反铁磁态的每个分子总的能量值要比处在铁磁态的能量值要小，因此反铁磁态是Fe{O（CH2CO2）2}（H2O）2（NO3）的基态，而铁磁状态只是一个亚稳态，这与实验结果一致的。

图2 铁磁态和反铁磁态的总态密度

图3 铁磁态和分态密度

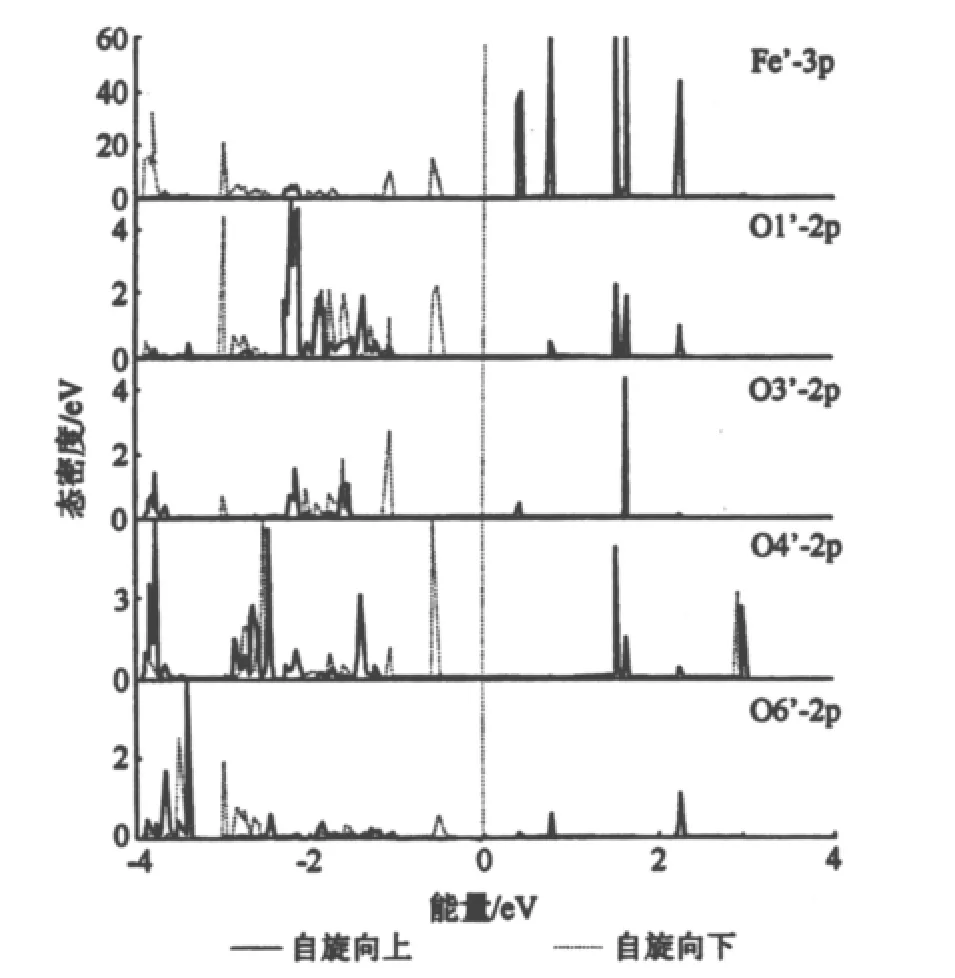
图4 反铁磁态的态密度

图2～4分别给出了铁磁态和反铁磁态分子的总态密度以及Fe离子和O离子铁磁态和反铁磁态的分态密度。总态密度图中能量范围为7～5eV，分态密度图中能量范围为-4～4eV，费米能级设为0，因为只有费米能级附近的态密度才决定化合物的磁性，因此把能量较低的芯态略去，重点研究费米能级附近的态密度。为了更好的研究磁作用，在图5中绘出了这2种状态的能带结构。从图5中可以明显的看出在铁磁态，最高占有分子轨道（HOMO）主要由铁离子和氧离子自旋向上的杂化态构成，而最低未占分子轨道（LUMO）则主要由铁离子和氧离子自旋向下的杂化态构成。自旋向上和自旋向下的态都没有穿越费米面。铁磁态自旋向上的态导带底能量为2.9eV，而价带顶的能量为-0.5eV，故带隙为3.4eV。铁磁态自旋向下的导带底的能量为0.4eV，而价带顶的能量为-1.2eV，因此它的带隙为1.6eV。反铁磁态导带底能量和价带顶能量分别和铁磁态自旋向下的导带底和自旋向上的价带顶相同，故它的带隙为0.9eV。因此，化合物Fe{O（CH2CO2）2}（H2O）2（NO3）为半导体。

图5 铁磁态和反铁磁态的能带结构

在费米能级附近，自旋向上和自旋向下的总的态密度明显劈裂。1个价带分裂成自旋向上和自旋向下2个子价带，这2个子价带的能量差大约为0.5eV，在图5里可以看得更清楚些。能量小于-1.1eV的部分，自旋劈裂的情况就不明显了。从铁离子的态密度图上，可以看出3d轨道自旋向上的5个能带全部处于被占有态，自旋向下的能带只有在-2eV左右的一部分处于被占有态，其余绝大部分为未占态，很明显铁离子处于高自旋态。

为了找出磁矩的来源，讨论原子中电子的排布是非常必要的。铁原子的核外电子排布为1s22s22p63s23d64s2，因此铁原子可以失去电子成为Fe3+或Fe2+离子。在不同的化合物中铁离子可能处于高自旋态也可能处于低自旋态，Fe3+离子高自旋态的外层电子排布为离子高自旋态的外层电子排布为本文计算结果表明Fe、O1、O3、O4、O6在铁磁态的磁矩分别为3.995 μB、0.113 μB、0.094 μB、0.105 μB、0.073 μB。反铁磁态分子内原子磁矩与铁磁态分子内各原子磁矩相同，只是相邻分子里对应原子磁矩符号发生了改变，大小并未改变，分别为-3.995 μB、-0.113 μB、-0.094 μB、-0.105 μB、-0.073 μB。因此可以断定分子的总磁矩主要来源于铁离子，而与之毗邻的氧离子对总磁矩的贡献则要小得多。因此铁离子在化合物Fe{O（CH2CO2）2}（H2O）2（NO3）中处于高自旋态。由于铁离子的磁矩为3.995 μB，所以它的最外层电子排布应为这意味着有5个自旋向上的电子和1个自旋向下的电子，铁离子总的自旋磁矩理论上应该为±4 μB。由于铁离子3 d壳层全部被占用，故二重态和三重态都有电子填充，因此轨道角动量的冻结效应非常明显，可以不用考虑轨道磁矩对总磁矩的贡献。

从图2中还可以看出铁离子的3 d轨道和周围的氧离子的2 p轨道在-0.5eV、-1.1eV、-2.0eV等处具有相似的峰值，这说明铁离子与周围的氧离子之间存在的轨道杂化现象。NO3离子的O4和O5形成共轭 π 轨道，O（CH2CO2）2离子中的O1、O3和O2也形成了共轭π轨道。该化合物是以铁离子为中心的配位化合物，外层电子排布应为为高自旋态，因此根据配位场理论可以判断该化合物为内轨配合物。配合物磁矩与未成对电子数的关系为

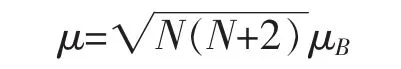
由于未成对电子数N为4，所以配合物分子总的磁矩应为4.9 μB，这与计算结果 4.99 μB基本一致。

Leonardo D.Slep等人通过电子自旋共振实验测得分子中Fe离子的自旋为5/2，这意味着铁离子有5个未成对的外层电子，应为Fe3+离子，3 d电子排布为，与判断明显不同。Leonardo D.Slep等人的实验结果表明，每个分子自旋磁矩接近于5 μB，这和实验结果 4.99 μB基本相符。虽然对于铁离子磁矩的判断，和Leonardo D.Slep等人不同，但分子的总的磁矩结果却一致。因此认为铁离子周围的氧离子以铁离子为中心形成几个配位大π键，自旋正好分布在这些共轭π轨道上，所以用电子自旋共振测量铁离子自旋时，不可避免的包含了周围的氧离子的自旋。正是这种杂化的结果使的氧离子产生了自旋磁矩，或者说使铁离子的自旋磁矩退局域化。图6在选定的主平面内画出了自旋密度图，其中实线和虚线分别代表自旋的正负。从图6可以明显的看出铁离子与周围的氧离子之间的铁磁相互作用及自旋退局域化情况。

图6 主平面的自旋密度

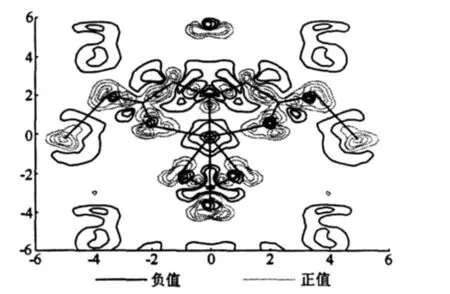
图7 主平面的差分电荷密度

化合物Fe{O（CH2CO2）2}（H2O）2（NO3）分子间成键作用比较弱而分子内的成键作用则比较强。电荷的转移可以通过差分电荷密度图看得很清楚。图7在选定的主平面内画出了成键前后电荷密度差值δρ（r）的等高线，原子位置同图6。从差分电荷密度图可以很明显得看出Fe和O之间的成键作用比较强，而分子之间的作用主要靠氢键维系。

为了验证该化合物的磁性与氢键的关系，在不改变分子结构及原子位置的基础上去掉产生分子间氢键的水分子再进行第一性原理的计算。结果发现，化合物总的磁矩不变，铁离子上的磁矩略有降低，变为3.833 μB，而与之毗邻的其他的氧离子的磁矩则略有提升。这说明氢键的作用仅仅限于提高了结构的稳定性，对物质的磁性质并无多大影响。同样在不改变分子结构及原子位置的基础之上，仅仅去掉产生分子间氢键的氢原子，保留与铁离子配位的O6再进行第一性原理计算。如果把O6的价电子数设为8，即不改变铁离子周围的配位情况，得到的磁矩分布结果跟氢键存在时一模一样。而如果把O6的价电子数设为6，很明显这样会使铁离子上的电荷分布发生很大变化，破坏了原来的配位情况，结果化合物变得无磁性。总而言之，氢键并不影响该化合物的磁性，铁离子的磁矩的大小跟其与周围的氧离子配位情况相关，由于铁离子上分布的配位电荷非常小，这种影响并不是很明显。

4 结 论

本文采用基于密度泛函理论的第一性原理方法，计算了化合物Fe{O（CH2CO2）2}（H2O）2（NO3）的电子结构和磁性质,并得到不同状态下化合物的能量、总态密度、分态密度、原子的自旋磁矩、以及自旋密度和差分电荷密度。结果显示该化合物是具有反铁磁基态和铁磁亚稳态的半导体。自旋磁矩主要来源于铁离子，分布在铁离子周围与其配位的氧离子对总的磁矩也有一定的贡献，分子总的自旋磁矩为4.99 μB，这个结果和实验也相吻合。氢键的存在维系了化合物的稳定性，但和分子磁性没有关系，作为顺磁中心的铁离子的磁矩大小，受配位情况的影响，但并不明显。

[1]O.Kahn.Molecular Magnetism[J].New York：Wiley-VCH，1993.

[2]S.J.Luo，K.L.Yao.First-principles studies on the conductive and ferromagnetic properties of MnIICuII bimetallic chains[J].Physics Letter A，2004，330：286-290.

[3]K.Doll，A.U.B.Wolter，H.H.Klauss.Electronic structure of the molecule-based magnet Cu PM（NO3）2（H2O）2[J].Physical review B 2007，75：184433-184439.

[4]L.Thomas，F.Lionti，R.Ballou，et al.Barbara，Macroscopic quantum tunneling of magnetization in a single crystal of nanomagnets[J].Nature（London），1996，383：145-147.

[5]J.R.Friedman，M.Psarachik，J.Tejada.Macroscopic Measurement of Resonant Magnetization Tunneling in High-Spin Molecules[J].Phys.Rev.Lett.，1996，76∶3830-3833.

[6]F.Wudl，G.M.Smith，E.J.Hufnagel.Bis-1，3-dithiolium chloride：an unusually stable organic radical cation[J].Chem.Commun.，1970：1453-1454.

[7]H.Shirakawa，et al.Synthesis of electrically conducting organic polymers∶halogen derivatives of polyacetylene，（CH）x[J].Chem.Commun.，1977：578-580.

[8]Leonardo D.Slep，Rafael Calvo，Otaciro R.A seven-coordinate FeIII compound：Fe{O（CH2CO2）2}（H2O）2（NO3）.Preparation，structure and magnetic properties[J].Inorganica Chimica Acta，2007，360：2911-2916.

[9]G.Kresse，J.Furthmpller.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Phys.Rev.B，1996，54：11169-11186.

[10]G.Kresse，D.Jouber.From ultrasoft pesudopotentials to the projector augmented-wave method[J].Phys.Rev.B，1999，59：1758-1775.