基于GLCM和CGA的人脸表情识别方法研究

田 儆， 余雪丽， 钱 杰

(1.中国联合网络通信有限公司河北省分公司，河北 石家庄050011;2.太原理工大学 计算机与软件学院，山西 太原030024;3.中国联合网络通信有限公司高碑店分公司，河北 保定074000)

人脸表情是人类进行情感交流的一种重要方式,从表情的变化中可以感知出人的情绪、感受、秉性和气质。自动化的人脸表情识别(FER)技术可以协助进行人脸识别、智能人机交互以及行为科学和医学研究等。根据所研究数据的不同,FER算法可以分为针对多幅图像和针对单幅图像两大类。由于单幅图像包含较少的表情信息,从单幅图像识别表情比从多幅图像中进行更具挑战性。然而,在有些情况下,单幅图像中已包含了足够的表情信息,而且计算相对简单。因此，本文主要探讨基于单幅图像的人脸表情识别。

人脸表情识别主要分为三个步骤：寻找感兴趣区域（ROI）、特征提取和表情图像分类。寻找感兴趣区域，目前常用的方法有基于模板匹配的方法和基于特征提取的方法，前者考虑图像全局；后者则考虑图像局部区域，主要考虑形状和纹理。通过特征提取过程降低维数，目前常用的方法有主成分分析 (PCA)、Gabor过滤等方法。通过对从ROI中提取出来的特征向量进行分类，目前常用的方法有神经网络(NN)、隐式马尔可夫链(HMM)和支持向量机(SVM)。上述基本方法使研究仅仅考虑到如何在各个步骤中优化算法,忽略了步骤之间的依赖性，因为先要选定ROI，然后再进行特征提取，所以步骤连接中需要人工干预。针对此问题,本文有效地利用CGA，通过CGA的不断迭代将前两步有机结合,实现了自动机制，并且简化了设计。

最近，HERNANDEZ B等[1]人提出利用灰度共生矩阵和遗传算法相结合的方法解决红外线图像上的人脸表情识别问题,其中存在一些不足之处：遗传算法中个体是随机产生的，造成个体在空间内分布的不均匀性，使得实验效果并不明显；仅可解决红外线图像。针对以上不足，本文首先将灰度共生矩阵拓展到可视化图像上，并用相应的实验数据证明其可行性。利用混沌的随机性、遍历性和规律性，将混沌原理加入遗传算法中，对传统遗传算法进行改进，有效地解决了个体分布的不均匀性，同时也没有忽略其差异性。经过理论推导和实验仿真，证明本文的方法是切实可行的。

1 灰度共生矩阵（GLCM）

纹理是图像分析中常用的特征，一般说来可以认为纹理由许多相互接近的、互相交织的元素组成，并具有一定的周期性。量化图像的纹理内容是描述图像的一种重要方法。基于统计的方法是纹理分析中最基本的一类方法，而基于灰度的共生矩阵法[2]又是一种典型有效的基于统计的纹理提取方法。因此，本文选取灰度共生矩阵来提取特征。

1.1 GLCM原理

定义1灰度共生矩阵表示了图像中相距(Δx,Δy)的两个灰度像素同时出现的联合概率分布，其中，Δx和Δy的范围大小由两个参数决定：像素间距d和方向角θ，其中，Δx=dcosθ，Δy=dsinθ。

对以上两个参数的选择并没有什么确定的算法，一般都考虑指定像素点邻域范围内的点。对于图像检索而言，由于像素的分布在各个方向上都可能不同，因此，宜采用 8-连通邻域[3]进行灰度共生矩阵计算,即 d=1，θ=0°、45°、90°、135°。

若将图像的灰度级定为 L级,则共生矩阵为 L×L矩阵，可表示为M(i,j)。其中，位于(i,j)的共生矩阵元素mij的值表示一个灰度为i而另一个灰度为j的两个相距为(Δx,Δy)的像素对出现的次数。对图像中的任一区域 R，定义S为其中具有特定空间联系的像素对的集合，则可定义共生矩阵：

共生矩阵M(i,j)归一化可得：

其 中 ，i∈[0,L-1],j∈[0,L-1]，x2=x1+dcosθ，y2=y1+dsinθ，#(S)表示集合S中对M(i,j)有贡献的元素的个数。取日本女性表情数据库JAFFE的一个“Happy”实例,如图1所示。

取灰度的量化级数为 8，d=1,θ=90°,它的灰度共生矩阵为：

行和列表示量化级数。

这样得到的矩阵可以反映不同像素相对位置的空间信息。共生矩阵中还包含了图像的纹理信息，对于具有不同特点的图像纹理，其灰度共生矩阵也会明显不同。对纹理较为粗糙的区域，其灰度共生矩阵中mij的值较集中于主对角线附近，对于粗糙纹理，像素对一般具有相同的灰度；而对于纹理较为细腻的区域，其灰度共生矩阵中mij的值则散布在各处,其像素对灰度差异较大。

1.2 GLCM用于表情识别的可行性分析

1978年，EKMAN和FRIESEN提出了面部表情编码系统（FACS），并研究了六种基本表情，即高兴、悲伤、惊讶、恐惧、愤怒和厌恶[4]。

表情变化的区域主要集中在眼睛、眉毛和嘴巴，因此，采用公式(1)选取 JAFFE 图库中“Neutral”、“Happy”、“Surprise”三种表情对三个主要集中区域之一的嘴部区域进行实验，如图2所示。

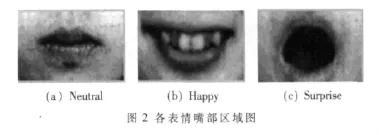
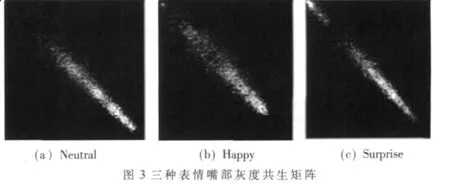
由以上三种表情嘴部区域所生成的灰度共生矩阵如图3所示。由图3可以看出，对于“Happy”这种表情来说，其嘴部区域的灰度值比之另外两种表情的嘴部区域变化要频繁，其图像的纹理特性相对属于“细纹理”。而另两种属于“粗纹理”，其灰度共生矩阵中的值较集中于主对角线附近。对于粗纹理，像素对趋于具有相同的灰度；而对于细纹理的区域，其灰度共生矩阵中的值则散布在各处。就“Neutral”与“Surprise”这两种表情而言，“Neutral”表情的嘴部区域口形较小，因为嘴附近肤色的缘故，其灰度值多处于高亮度区域，反映在灰度共生矩阵上则是主对角线上小序号行列的数值较低，连通性较差。而“Surprise”表情的嘴部区域口形较大，其灰度值多处于低亮度区域，因而其灰度共生矩阵主对角线上数值比较均衡，连通性较好。

由此可见，用灰度共生矩阵可以反应出各种表情之间的差异，不难想象从中提取出的各种统计量就可以作为表情特性的度量。

1.3 特征向量

当区域R中像素点过多时，会导致维数过高很难处理，因此通常采用以下几个特征量表示。

(1)反差(Contrast)：

(2)能量(Energy)：

(3)熵(Entropy)：

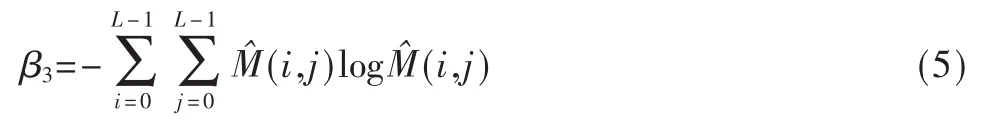
(4)一致性（Homogeneity）：

(5)相关(Correlation)：

式中 μ1、 μ2、σ1和 σ2分别定义为：

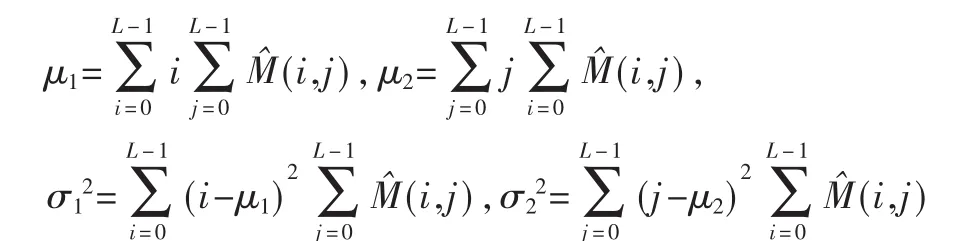
其中，L为各个分量的量化级数，即上述求出的GLCM矩阵中行和列的值，即L=8。因此，提取出的R的特征向量表示为={β1，…，β5}。

2 支持向量机（SVM）

支持向量机(SVM)起初由VAPNIK提出时，是作为寻求最优(在一定程度上)二分类器的一种技术，后来它又被拓展到回归和聚类应用。

2.1SVM定义

定义2 SVM是一种基于核函数的方法，它通过某些核函数把特征向量映射到高维空间，然后建立一个线性判别函数（或者说是一个高维空间中的能够区分训练数据的最优超平面）。解是最优的在某种意义上是两类中距离分割面最近的特征向量和分割面的距离最大化。离分割面最近的特征向量被称为“支撑向量”，意即其他向量不影响分割面（决策函数）。假定有一些分好类的训练数据集{xi,yi},i=1,…,m,yi∈{-1,+1},xi∈Rd,最优超平面通过以下公式求得：

其中，xi是支持向量，yi是它相应的类别，K(xi,x)是核函数，通用的核函数类型有线性核函数、多项式核函数、径向基函数和sigmoid函数。由于径向基函数在划分非线性问题时比其他函数性能优越，在此采用径向基函数，即

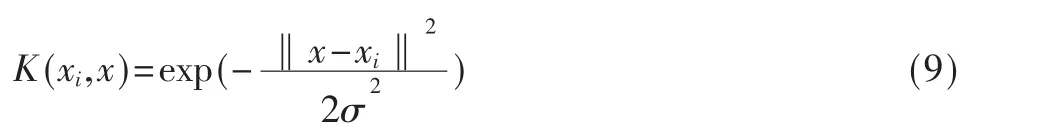
f(x)的输出符号表明x的所属类别。

2.2SVM多分类方法

SVM算法最初是为二值分类问题设计的，当处理多类问题时，就需要构造合适的多类分类器。目前，构造SVM多类分类器的方法主要有两类：一类是直接法，直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类，这种方法看似简单，但其计算复杂度比较高，实现起来比较困难，只适用于小型问题中；另一类是间接法，主要是通过组合多个二分类器来实现多分类器的构造常见的方法有两种。(1)一对多法（one-versus-rest）。训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。(2)一对一法(one-versus-one）。其做法是在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时，得票最多的类别即为该未知样本的类别。除了以上两种方法外，还有有向无环图DAG(Directed Acyclic Graph)和对类别进行二进制编码的纠错编码(Error Correcting Code)。本文采用第二种方法并结合投票策略(voting scheme)[5]来设计需要的多分类器。

2.3 k-折交叉验证（K-fold cross-validation）

由于我们的数据样本集较小，因此引入k-折交叉验证。

定义3 k-折交叉验证是指将样本集分为k份，其中k-1份作为训练数据集，而另外的1份作为验证数据集。用验证集来验证所得分类器或者回归的错误码率。一般需要循环k次，直到所有k份数据全部被选择一遍为止。

3 混沌遗传优化算法（CGA）

3.1 遗传算法的改进

遗传算法是一种模拟生物进化过程的优化方法,它能在有限代数的进化过程中,在全局解空间内自动进行搜索得到最优解或是次优解。它可以通过编码技术,将具体的问题抽象处理,仅对编码串进行操作,在进化过程中以适应度作为标准,从而避开了问题的复杂优化判别准则。但是遗传算法对初始种群最初是采用一种随机方式产生的,这些个体在解空间内分布可能不均匀,为了使遗传算法能在解空间内更好地进行全局搜索,杨宇明等人[6]提出一种新的随机个体产生方法，将混沌原理引入遗传算法。混沌具有随机性、遍历性和规律性,用它产生初始种群会提高遗传算法的效率,使遗传算法的初始种群不再随机产生,而是由混沌产生。混沌是一种非线性的映射,它看似随机的过程,其实质是一种有着内在机制的运动过程。因此，本文也将混沌原理引入，对遗传算法进行改进，采用logostic映射表示混沌的系统：

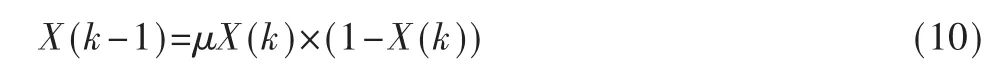
当μ=4时,这个系统是一个完全混沌系统,它没有稳定解,而且是一个满映射的过程。这些特性能够提高遗传算法初始种群的差异性。混沌遗传优化算法过程[7]如图4所示。

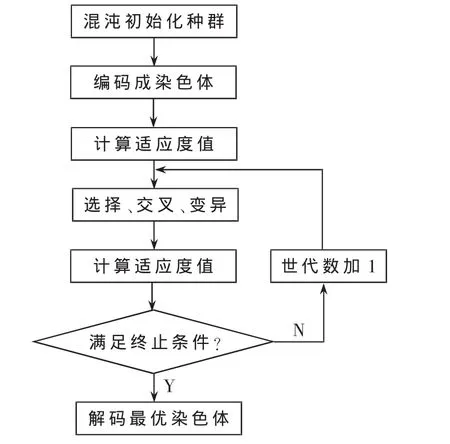
图4 混沌遗传优化算法流程图

3.2 适应度函数（Fitness function）

GA应用于实际问题时,适应度函数的定义往往最为困难，而且其计算复杂程度对于整个GA的搜索时间有较大影响。本文方法的目标就是寻找最佳的ROI，在ROI上面提取特征用于分类。因此，每个选定的ROI分类的正确性对适应度函数起至关重要的作用。然而，当两个不同的解决方法得到同样的分类正确性时，为了简化计算应该选择特征值数量较少者，因此，本文适应度函数[8]设计如下：

其中，Accuracy为对于给定个体所有SVM的平均正确率，可由k-折交叉验证[5]求得;Zeros为染色体中起作用的特征值数量。

3.3 选择、交叉和变异

选择方法：假设群体规模为N，经交叉、变异操作后产生N个子代个体。将子父代组成的2N个群体按适应度函数值从大到小排序，取前面N/2个个体放入配对池，再从后面的N个个体中随机地选出N/2个个体放入配对池。由于既选择到适应度函数的较大值又选择到适应度函数的较小值，这样，既可保证种群向最优解收敛，又可保证种群的多样性不会迅速减少。

变异算子选择：为了简化实验，提高实验性能，本文采用基本位变异作为变异算子，即以变异概率对个体编码串中基因座上的基因值做变异运算。

交叉算子选择：同样为了简化实验提高实验性能，本文的交叉算子采用单点杂交算子[10]，在个体编码串中随机设置一个杂交点，然后进行部分基因变换。

4 算法描述

(1)染色体编码，产生初始化种群。用混沌遗传优化算法进行感兴趣区域(ROI)选择和特征提取。CGA选出一个集合 Ω，其中含有 n个 ROI,在此 n=5，ROI用 w1,…,w5表示,wi为1表示激活，wi为0表示没有激活。每条染色体编码[9]如下，定义 5个变量{c1,…,c5}，每个变量用1 bit编码，每一个变量决定对应的wi是否被激活。每个wi包含4个参数 {xwi,ywi,hwi,wwi},由于预处理图片到32×32，因此每个参数用 5 bit表示。其中，(xwi,ywi)表示ROI的起始点坐标，hwi表示ROI的高度，wwi表示ROI的宽度。βwi,j为从 wi中提取的第 j个特征值大小，αwi,j表示 βwi,j是否被激活，1表示激活，0表示没有激活,以此来寻找5个特征值的最佳组合。染色体编码方式如图5所示，因此染色体长度为：5+5×4×5+5×5=130。基于以上编码方式和公式(10)混沌产生初始化种群，每个个体对应预处理后图片的感兴趣区域。

(2)GLCM参数选择。灰度共生矩阵的参数：像素间距 d 和方向角 θ，因为 i=[1，5]，∀wi∈Ω，考虑 8-连通邻域，所以取 dwi=1，θwi=90°。 在这个过程中，CGA通过调整灰度共生矩阵的参数来进行特征构建。

具体方法为：对每个个体中的由wi激活的ROI利用公式(1)计算其灰度共生矩阵，再利用式(2)进行归一化，利用计算出 来的(i,j)，按 照式(3)、式(4)、式(5)、式(6)、式(7)求 得 其 特 征 向 量，即=(β1，… ，β5)，其 中 ，∀wi∈Ω。集合 Γ={}用于分类。这一过程中，利用CGA将ROI的选择和特征提取结合在一起。

(3)支持向量机和k-折交叉验证。给定一个训练样本集(多幅已经分好类的图像),将其平均分成 k份，其中k-1份作为训练数据集，而另外的1份作为验证数据集。对每个wi由激活的ROI，用验证集来验证所得分类器的正确性，一般需要循环k次,直到所有k份数据全部被选择一遍为止。在此，选取k=6。根据求得分类器的正确性利用公式(11)计算适应度，在此，Zeros=∑i∑jβwi,jwi，i=1,…,5，j=1,…,5，按照 图 4 的 流程 执行遗 传 算 法的流程,最终可以得到一个满足所要求条件的最佳个体。通过调整实验参数,选定交叉概率为0.66,变异概率为0.05。

(4)利用选择出的最佳个体和训练样本集再次训练SVM，然后用训练好的SVM可以对未在样本集中的未知图像进行分类。

整体算法流程图如图6所示。

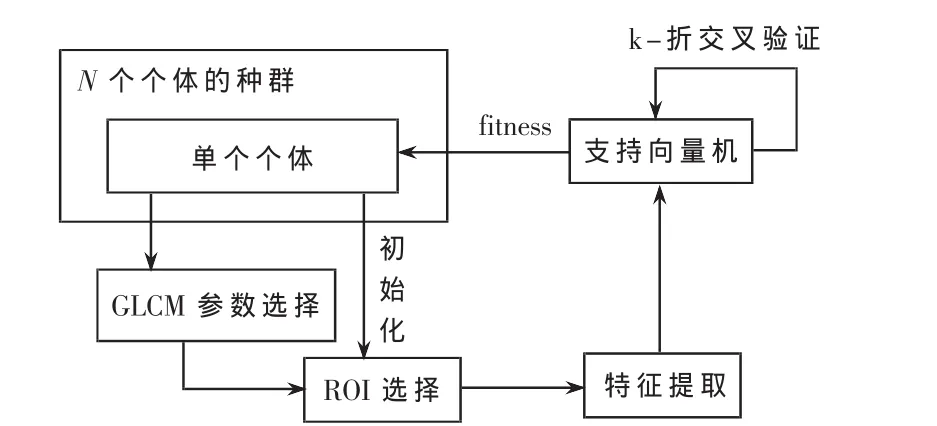
图6 算法流程图

5 实验结果及分析

本文选用Matlab 7.0为实验平台，从JAFFE图库中选出“Happy”、“Neutral” 、“Angry”和“Surprise”四种表情的图像样本共 121幅，其中：“Happy”表情 31幅、“Neutral”表情 30 幅、“Angry”表情 30 幅、“Surprise”表情 30幅。从这些图像样本中选择“Happy”表情 16幅、“Neutral”表情 15 幅、“Angry”表 情 15 幅 、“Surprise”表情 15幅共61幅作为训练样本,剩余每种表情 15幅，共 60幅作为测试样本。经过实验选定种群大小为50，最大遗传代数为50，经过三次实验，求得的识别率如表1所示。

由表1不难得出，采用灰度共生矩阵特征值表征的特征对“Happy”和“Neutral”识别效果较为理想，对于“Angry”也有较高的识别率，对“Surprise”识别率较低。总体来说，本文提出的基于灰度共生矩阵和混沌遗传优化算法相结合的算法能够得到81.67%的平均识别率，识别结果令人满意。最优个体的感兴趣区域数目为2，参数为{14 16 13 15}和 {19 3 9 25}，分别对应中心点坐标(xwi,ywi)、ROI宽度 hwi和 ROI高度 wwi。最优个体ROI在JAFFE库上一个实例的区域截图如图7所示。

表1 特征识别结果

本文提出了利用CGA将ROI的选取和特征的提取有机地结合，通过不断调整灰度共生矩阵的参数寻找最优个体，利用最优个体标明的ROI训练SVM，最后通过SVM进行分类。该方法的优点在于能够很好地利用人脸表情处理步骤之间的依赖性，将前两个步骤有机地结合成一步，消除了步骤连接中的人为因素，实现了自动机制，并且简化了设计，而且将混沌原理引入遗传算法当中，有效地解决了随机产生个体的不均匀性，又保持了个体的差异性。通过定理、公式推导和实验仿真，证明该方法切实可行。

[1]HERNANDEZ B,OLAGUE G,HAMMOUD R,et al.Visual learning of texture descriptors for facial expression recognition in thermal imagery[J].Computer Vision and Image Understanding,2007(106)：258-269.

[2]谢红薇,田儆,余雪丽,等.基于 MCM和 CGA的人脸表情识别方法研究[J].微电子学与计算机,2008,25(12)：45-49.

[3]冷冰.基于形状和纹理的微生物菌种图像智能检索系统研究[C].visionchina 2006机器视觉会议,2006，6.

[4]EKMAN P,FRIENSEN W.Facial action coding system：A technique for the measurement of facial movement[J].Consulting Psychologists Press.1978.

[5]刘晓旻,章毓晋.基于Gabor直方图特征和MVBoost的人脸表情识别[J].计算机研究与发展,2007(7)：1089-1096.

[6]杨宇明,李传东.混沌在遗传算法中的应用[J].计算机工程与应用,2004,40(5)：76-77.

[7]吴建华,李娜,李静辉,等.基于 CGA和 ICA的人脸特征提取方法研究[J].计算机应用,2007,27(8)：2038-2040.

[8]SUN Z,BEBIS G,MILLER R.Object detection using feature subset selection[J].Pattern Recognition,2004,37(11)：2165-2176.

[9]唐旭晟,欧宗瑛,苏铁明,等.基于AdaBoost和遗传算法的快速人脸定位算法[J].华南理工大学学报，2007,35(1)：64-69.

[10]潘正君.演化计算[M].北京：清华大学出版社,1998.