基于双混沌映射的图像加密算法

唐立法，周健勇

(上海理工大学 管理学院，上海 200093)

数字图像信息具有直观、形象、易懂和信息量大等特点，已成为人们日常生活、生产中接触最多的信息种类之一[1]。随着数字图像在商业、军事等不同程度的保密领域内的普及，其安全性研究得到了广泛的关注[2]。由于图像存储的特殊性，在传统的密码学领域并没有单独将图像作为一种特殊的明文形式来考虑其加密特性。虽然利用传统的加密技术对图像加密是可实现的，但其加密效率低、安全性不高，不能适应图像加密的需要，因此专用的图像加密技术被广泛关注。近年来混沌理论的应用研究引起了密码学界的关注，由于混沌遍历性正符合Shannon提出的密码系统设计的扩散混淆等基本原则，使混沌理论在图像加密中得到广泛应用[3-5]。本文提出一种基于Logistic和Henon双混沌的图像加密算法，并通过实验分析证明，该算法具有优异的加密性能和运算效率。

1 混沌理论及模型

混沌与密码学有着紧密的联系，一个好的密码系统应该具备以下几个条件[6]：(1)把明文变换为尽可能随机的密文；(2)加密算法对明文有高度敏感性；(3)加密系统对密钥有高度敏感性。由于混沌具有对初值的敏感性、良好的伪随机特性、轨道的不可预测性等特征，这些特征正好能够满足密码系统的要求。

Logistic映射是一个非常简单却具有重要意义的非线性迭代方程，虽然它具有确定的方程形式，不包含任何不确定因素，却能产生完全随机的、对参数μ的动态变化和初值极为敏感的序列。其定义如下：

式中，xn∈[0，1]， 系统参数 μ∈(0，4]。 当 3.569 946…≤μ≤4时，该映射产生混沌序列。混沌映射产生的序列对初始值极度敏感，对于相差的初始值，方程迭代出来的轨迹差别相差很明显，一般情况下，很难从一段有限长度的序列来推断出混沌系统的初始条件。该混沌模型迭代方程简单，混沌加密参数只有一个，这决定了其加密运算速度快，特别是比高维的混沌系统要快很多，但其密钥空间比较小，安全性稍差，因此不考虑单独使用它。

Henon混沌系统是1976年由Henon提出的一种二维迭代系统，具有两个参数的平面映射族。Henon混沌映射定义如下：

式中，a、b 为控制参数，当 1.05＜a＜1.8、b=0.3 时，Henon映射处于混沌状态[7]。当处于混沌时，它与Logistic模型同样具有混沌的特性，不同的是Henon映射是一个具有两个参数的平面映射族。虽然理论上对Henon混沌的研究比较成熟，但是由于其产生混沌序列的特殊性，一般也不单独使用。

2 加密解密矩阵的构造

由于单混沌存在诸多缺陷，密钥空间小，且在有限精度的系统下受限制，参考文献[8]表明，单混沌映射加密易受到攻击利用。因此，本文利用Logistic和Henon双混沌系统来构造加密矩阵实现对图像加密。首先对Logistic混沌系统产生的序列通过一种动态量化得到置换矩阵的随机数，对图像的像素位置置乱；再通过Henon混沌系统的映射，利用整数求余的量化方法来得到“异或”加密的随机数，与置乱后的图像依次“异或”。图像加密效果完全取决于两种混沌系统产生的随机数，因此，对Logistic混沌的动态量化和Henon的整数求余量化成为实现加密效果的关键。

设原始图像为I，大小为 m×n，则图像 I可以表示为：I=F(i，j)(0≤i≤m，0≤j≤n)。其中，(i，j)表示像素点位置，F(i，j)表示该点处图像的数据，则 F(i，j)可构成图像数据矩阵T。

2.1 置换矩阵的构造

首先利用一种随机全排列生成算法来生成置换加密中所需的全排列。所谓全排列即是将M个不同元素按照一定的顺序排列起来，称为这M个不同元素的一个全排列。本置换方法分为行置换和列置换，行置换算法描述如下：

(1)设生成的置换矩阵大小为m×n，首先要生成一个0～M-1之间的全排列元素，元素数目为 M(M＞n)。

(2)初始化全排列矩阵，令{0，1，…，M-1}中所有元素的一个全排列为{a0，a1，…，aM-1}，当 i≠j时，有 ai≠aj。全排列初始值系数为 L，令 n=⎿L×M」，L可以当密钥给出，一般 L在(0.5，0.7)区间即可。若太小，则产生的全排列随机性差；若太大，则数据重复多，将会增加系统的迭代次数。

(3)设所用混沌系统方程为 xn=f(xn-1)，本文用的是Logistic混沌模型，xn即为当前混沌序列，每次都要进行迭代来产生新的混沌序列。利用不等分区间的动态量化对混沌序列进行进一步处理，以增强其随机性和复杂度，本文利用参考文献[9]的判决公式(3)对Logistic混沌方程式(1)产生的序列{xn}进行判决，可以得到K=2n进制伪随机序列{σc(xn)}：

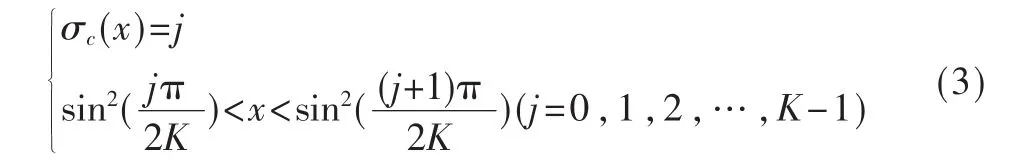
定义序列{xn}经过判决所在的位置构成序列为Pn={p1，p2，…，pn}，其中 Pi=j，即每一个 xi都和一个 xpi相对应，可进行两个位置元素交换，然后再重新判决，通过这样的量化即可得到n个0～M-1之间的随机数。

(4)初始化一个数组A，初始为空，最大长度为m，将步骤(2)生成的元素依次添加到A中，若A中不存在生成的元素，则添加到A末尾，否则舍弃。直到A中元素为n个，然后将0～M-1间元素不在A中的依次添加到A中，形成初始化全排列A。

(5)对初始化全排列A再进行一次全变换来增强随机性，方法同步骤(2)，即将两个对应位置元素A[Pi]同A[Ppi]的交换。这里全变换的次数可以自行设定，但考虑系统运行的速度，全变换轮数r不宜过大，一般不超过5轮，由密钥给出。

(6)反复执行步骤(3)、(4)、(5)可得到一个 m行随机全排列，即可构成m×n大小的行置换矩阵A′。

(7)行置换方法可看作函数 B=E(A′，T)，其中 B为加密后矩阵，即是将 T[i，j]的值赋给 B[i，Ppj]。 列置换的方法和行置换方法相同，在此不再描述。设矩阵B经过列置换 后为 B′m×n。

该算法生成的全排列对混沌系统的初值敏感，密钥的细微差别都将产生不同的全排列。利用该算法可以生成任意多所需长度的随机全排列，算法中细微部分可以灵活处理，以增强密钥强度。

2.2 “异或”矩阵的构造

利用Henon映射进行迭代产生随机数构成 “异或”矩阵。由于Henon映射有一定的局限性，参考文献[10]对常用的几种混沌模型产生的序列进行随机性测试，得出Henon混沌映射的随机性强度并不是十分理想。因此，本文用Henon混沌序列进行扰动变换后产生相关序列及参数，将输出结果进行整数取余进一步量化得到“异或”矩阵。其中部分细节可以灵活变换修改，在此不作详细规定。

(1)初始化混沌系统方程(2)的参数，舍弃前若干次迭代的混沌序列，得到随机序列 x′n、y′n。

(2)根据 z′n=α×x′n+(1-α)×y′n(0＜α＜1，α 为系统参数)将 x′n、y′n进行扰动得出输出序列 z′n。

(3)利用整数求余量化从z′n获取所需要的随机数。设z′n小数点后的位数为k，取出其中任意t个序列组成一个数对m求余即得到一个0～m-1内的随机数，一般3≤t≤7，且 t≤k，m＜10t。

(4)反复执行步骤(1)、(2)、(3)，直到构成大小为 m×n的“异或”矩阵所需随机数，设得到的“异或”矩阵为Cm×n。

(5)将“异或”矩阵 Cm×n与所得的置换矩阵 B′m×n逐一“异或”即可得到加密矩阵。

“异或”矩阵的使用增强了整个算法的安全性。置换矩阵和“异或”矩阵的使用，进一步增强了加密效果，使抗攻击能力得到增强。

2.3 解密算法

解密算法是加密算法的逆运算，在解密算法中，置换矩阵是加密算法中置换矩阵的逆置换，“异或”矩阵与加密中的“异或”矩阵相同，只是在解密过程中要先进行“异或”运算，最后再进行“异或”运算。

3 仿真实验及测试分析

3.1 加密效果

本文采用大小为256×256、8 bit大小的Lena灰度图像作为待测试图像。密钥选取参数如下：x0=0.0798975229263307，μ0=4，r=1，x′0=0.790 408 305 649 9，y′0=0.210 030 319 169 164，t=3，分别取小数点后3、5、7位。原始图像及其灰度直方图分别如图1、图3所示，加密后的图像和灰度直方图分别如图2、图4所示。从图中可以看出，加密后的图像效果很好，各像素的灰度值分布均匀，与原始图像完全不同，对已知明文攻击非常安全。

3.2 敏感性分析

图5为正确密钥解密所得图像，通过比较可知，与原图的像素值完全相同，表明该算法没有信息的丢失。当密钥中的x0=0.079 897 522 926 300 6、其他密钥参数不变时，解密所得图像如图6所示。可见即使使用与正确密钥差值微小错误的密钥进行解密，得到的仍是与原图像差别很大的错误图像，即说明本文所用算法对密钥具有高度的敏感性。

3.3 图像剪裁测试

从解密后的图像中，剪裁掉右上角25%大小后的图像如图 7所示，剪裁掉中间一个大小为 100×100后的图像如图9所示。经解密后的图像分别如图8、图10所示。可以看出，对密文进行剪裁干扰后进行恢复，恢复后的图像也能很清楚地反映原始图像的一些特征，而且密文集中剪裁出的点都分散到原图像的不同位置，说明对图像的加密效果比较理想。

3.4 图像相关性分析

为了分析原图像与密文图像的相邻像素相关性，在水平、垂直和对角线方向上分别从原始图像和密文图像中随机选择2 000对相邻的像素点，并按照参考文献[10]中公式计算相关性，图 11、图12分别是图像加密前后 3个方向(水平方向、垂直方向、对角线方向)的相邻像素相关性。

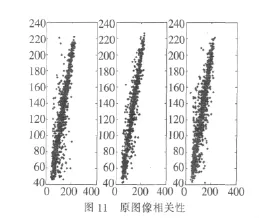
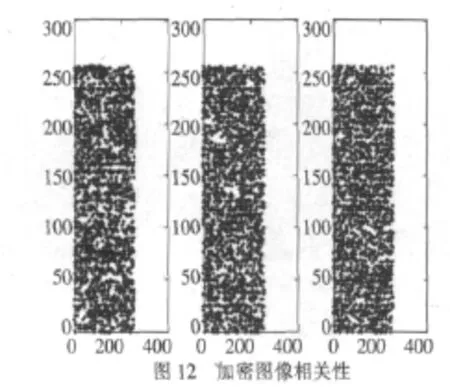
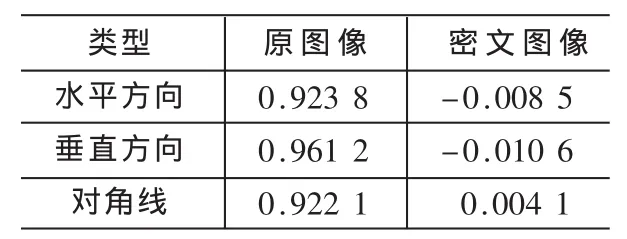
表1 相关性系数

表1为按3个方向计算所得的相关系数结果。由结果可知，原始明文图像相邻像素是高度相关的，相关系数接近于1。而加密图像的相邻像素相关系数接近于0，相邻像素已基本不相关，说明明文的统计特征已被扩散到随机的密文中。

本文提出基于双混沌映射的图像加密方法，充分利用混沌映射的性质实现图像的加密。相对于传统的单一混沌映射，密钥空间选择更广，提高了密钥流的线性复杂度，很大程度上增强了图像加密的效果。实验及测试分析证明，本方法简单易行、可靠性和安全性较好。

[1]JAIN A K.著.数字图像处理基础[M].韩博，等译.北京：清华大学出版社，2006.

[2]廖晓峰.混沌密码学原理及其应用[M].北京：科学出版社，2009：232.

[3]MATTEWS R.On the derivation of a chaos encryptional algorithm[J].Cryptologia， 1989，13：29-42.

[4]李国辉，徐得名，周世平.随机性参数自适应的混沌同步[J].物理学报，2004，53(2)：379-382.

[5]曹美君，张宏.混沌理论在数据加密中的应用[J].信息技术，2009(6)：169-171.

[6]钟华.基于混沌技术的图像加密研究[D].长沙：长沙理工大学，2006.

[7]HENON M.A two-dimensionalmappingwith strange attractor[J].Communication in Mathematical Physics，1978(50)：69-70.

[8]CHEN G，MAO Y.A symmetric image encryption scheme based on 3D chaotic cat maps[J].Chaos， Solitons and Fractals，2004(21)：749-761.

[9]冯明库，薛迎宵.混沌吸引子随机性的一种判别方法[J].计算机工程与应用，2007，43(15)：56-58.

[10]蔡觉平，李赞，宋文涛.一种混沌伪随机序列复杂度分析法[J].物理学报，2003，52(8).