一种改进的多目标粒子群组卷算法*

2010-11-27马跃亮靳志强孙晨霞

网络安全与数据管理 2010年23期

马跃亮，靳志强，孙晨霞

(河北农业大学信息科学与技术学院，河北保定 071001)

利用计算机按照一定的组卷算法从试题库抽取试题组成符合要求的试卷，是实现考试规范化和科学化的手段。在各种计算机辅助考试系统、试题库系统软件中，自动组卷一直是该类系统的一个难点，其解决方法也一直是算法研究热点。可以说一个自动组卷系统的效率和组卷质量主要取决于组卷算法。以往的组卷算法多采用随机抽题法、回溯试探法及遗传算法。

随机抽题法根据状态空间的控制指标，随机抽选一道试题加入试卷中，不断重复直到组卷完毕或失败为止。该算法简单，但是当题库庞大时，时间复杂度大，而且常由于约束条件的局部满足而导致组卷失败。回朔试探法是将随机选取产生的每一状态记录下来，搜索失败时，释放上次记录的状态类型，然后再依据一定的规律变换一种新的状态进行试探，通过不断地回朔试探直到试题生成完毕或回到出发点为止。当试卷总题量较大时，时间和空间复杂度都很大。可以看出，随机抽题法和回溯试探法都具有较大的缺点，而且不具有智能性。

遗传算法[1](GA)模仿自然界的适者生存法则，根据遗传的变异交叉等操作进行重复迭代，直到满足某些收敛指标。GA最初用于函数优化及组合优化。现已广泛用于生产调度问题、图像处理、人工生命、遗传编码和机器学习等领域。其在计算机辅助教学方面的应用也是一大亮点，如在组卷应用中远优于以往算法，但也存在粒子速度控制等问题。

1 组卷问题数学模型

1.1 组卷问题描述

组卷问题即计算机根据要求从题库中自动抽取符合条件的分数、难度、章节、知识点等要求的试题组成试卷，因此，组卷问题包括了多个重要指标，如分数、难度、题型、章节、知识点等。每道题在录入时已经被赋予了相应的指标。在本库中，试题分为1、2、3、4四个难度等级；试卷难度从难到易分为 A、B、C、D、E五个等级，每种级别的试卷中四种级别的试题所占比例不同。试题其他属性，如题型、章节、知识点等也都相应赋值。

1.2 数学模型

本文引用了王一萍[2]选用的关于粒子群算法设计的目标函数数学模型：

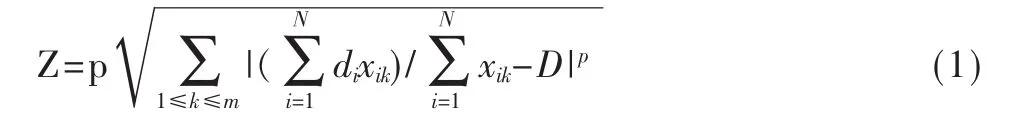
其他限制函数如下：

其中 xik表示试题，cik表示知识点，hik表示知识点覆盖率，dik表示难度系数，D表示目标难度系数，si表示主观题，ui为主观题最小比例。

在上面各式中，式(1)为目标函数，式(2)为主观题比例函数，式(3)为知识点覆盖率函数，式(4)为题型分布函数。

2 改进的粒子群优化算法

2.1 简单粒子群优化算法

假设在一个M维的目标搜索空间[3]中有n个粒子，每个粒子的位置表示一个潜在的解。用 xi=(xi1，xi2……xiM)表示第 i个粒子的位置向量。用 νi=(νi1，νi2……νiM)表示第i个粒子飞行的速度向量。将xi带入适应度函数f(x)就可以计算出其适应值 f(xi)，根据适应值的大小即可衡量 xi的优劣。用 pi=(pi1，pi2……piM)表示第 i个粒子迄今为止搜索到的最好位置，也称为个体极值pbest。用pg=(pg1，pg2……pgM)表示整个粒子群迄今为止搜索到的最优位置，也称为全局极值gbest。第i个粒子第m个分量根据下面公式来更新自己的速度和位置：

其中，νim(k)表示第 i个粒子在第k次迭代中第 d维的速度分量；xim(k)表示第i个粒子在第k次迭代中第m维的位置分量；c1和 c2为加速度系数；r1和 r2是介于[0，1]之间的随机数；ω称为惯性因子；ωνim(k)表示第 i个粒子在第k次迭代中第m维的惯性速度；pim(k)-xim(k)表示第i个粒子当前位置与自己最好位置之间的距离，作为第k+1次迭代源于第i个粒子本身的加速度；pgm(k)-xim(k)表示第i个粒子当前位置与群体最佳位置之间的距离，作为第k+1次迭代源于整个群体的加速度。据上式知，第i个粒子在第k+1次迭代中的位置和速度根据第k次迭代的位置 xi(k)、第k次迭代的速度 νi(k)、个体极值pbest、全局极值 gbest等生成。

由式(5)可见，粒子的速度进化方程由个体认知和社会信息共享两部分组成。

式(5)中的第一项 νim(k)为粒子更新前的速度，第二项c1r1(pim(k)-xim(k))为粒子本身的个体认知部分；第三项c2r2(pgm(k)-xgm(k))为粒子间的社会信息共享部分。如果进化方程只有个体认知部分，则因粒子间缺少信息交流，得到最优解的概率非常小；如果只有社会信息共享部分，则粒子因无自身的认知能力，虽然收敛速度较快，但粒子速度难以得到更理想的控制。

2.2 改进的粒子群算法

在整个粒子群寻优过程中，粒子飞行速度大小直接影响算法的全局收敛性。飞行速度大，则粒子到达全局最优解所需时间短，但容易飞越最优解；飞行速度小，则粒子到达全局最优解的时间长，故必需对粒子的飞行速度进行有效控制，使粒子在先期以较快速度飞行到全局最优区域，进而以较小的步长对最优区域进行局部搜索以获得高精度解。笔者将粒子群优化过程分为三个阶段。首先利用遗传算法的交叉操作对粒子群进行前期搅动，使得初始种群能够迅速地均匀遍布整个搜索空间；然后用变异操作进行局部寻优的微调搅动，使得种群更快地向目标移动靠拢；最后利用粒子群优化得出结果。

改进粒子群优化算法的实现步骤如下。

(1)随机生成初始群体

在粒子群算法中，每个粒子均表示一个可行解，以二进制编码形式表示。

在矩阵中，行表示试题，如：a2i为1表示试题 Qi在第2套试卷中被选择，每行表示一套试卷。每列依次表示题分、题型、章节、难度系数。

(2)计算并评价每个粒子的适应值

模型最初目标函数值用来衡量满足式(2)～式(4)候选解的质量。然而，基于粒子群优化算法的粒子可能不满足其中一个或多个限制条件。为解决此问题，评估粒子质量时，如果不满足某限制条件则要考虑惩罚函数，惩罚函数对应各限制条件。

①b罚值是关于不满足知识点限制范围：

这个值是弥补所选择试题知识点覆盖率的不足。

②d罚值是违反多试卷同试题数量的限制：

当两套试卷具有相同的试题数量超阈值S时使用。

③函数J(x)是计算粒子x适应值

J(x)=Z当满足所有限制条件

其中w1、w2和w3是相关的权重，同样粒子x的适应值要考虑目标值和罚值。根据组卷的实际问题，适应值越小，粒子越好。

(3)个体极值pbest和全局极值 gbest计算

使用限制标准确定pbest和gbest的值在原来的粒子群优化算法中，粒子的pbest和gbest最费时间，因此提出限制标准来加速确定粒子pbest和gbest的进行。根据分析得知，一个粒子的适应值是为了确定粒子pbest和gbest，但不能直接用于粒子速度的更新。因为Z和J(x)都能单独提高作用，可用当前pbest的适应值作为适应值的界限，当中间适应值超过此界限时则终止对第i个粒子适应值的计算。将第i个粒子的当前适应值与pbest值比较，如果优于它原来的pbest则用这个适应值更新其pbest，这种限制能节省计算时间。

(4)若个体极值pbest和全局极值 gbest满足条件或其他终止条件，则退出。

(5)将个体按照适应度排序，取适应度较差的50%进行交叉或变异操作，遗传操作计数器加1。

为加速粒子群初期的寻优速度，在前期加入遗传算法的交叉和变异操作。将排序后的50%粒子复制一遍，并与原型随机进行交叉或变异操作，然后再按适应度排序，取适应度值前50%放入原种群，保持种群规模不变。在总循环次数的前25%次，交叉率取0.8进行交叉操作，使群体迅速均匀地进行全局搜索；接下来的15%次以变异率为0.2进行变异操作，使得群体能更加快速地进行局部搜索。

①染色体的交叉。采用双点交叉运算[4]，随机选取两个双亲染色体确定两个随机交叉点进行交叉运算得出新个体，如：