多边形的边界单线搜索特征

李 丽, 张远平, 李 鹏

(兰州理工大学计算机与通信学院，中国 兰州 730050)

多边形搜索是计算几何中的一类基本问题，这类问题考虑的是如何利用一个或多个移动的搜索者(搜索者有不同的视觉范围)对一个多边形进行搜索以便检测到移动的入侵者．搜索者和入侵者均可用一个点表示，都可以在多边形区域内连续、任意地移动．文献[1]中提出了各种不同的搜索者模型．对于任意的一个整数k≥1，k线搜索者(k-searcher)可以通过发出束光进行搜索，全视觉搜索者(∞-searcher)的视觉范围为360°，边界单线搜索者只能沿多边形的边界移动且只能发出一束光．

多边形搜索问题[1]最初由Suzuki和Yamashita在1992年提出．由于应用广泛，如航海、安全防御、目标探测和追踪等等，该问题得到很多关注[2-3]．2000年Lavalle提出了一种基于可视图思想的算法[4]，以此来检测一个多边形是否可被一个边界单线搜索者搜索，其方法需要O(n2)的时间和空间．2003年Tan将上述时间复杂度降到O(nlogn)，空间复杂度降到O(n)[5]，但证明过程比较复杂．2006年Kamada利用可视图的思想证明了3种不可被一个边界单线搜索者搜索的模型[6]，虽然时间复杂度仍为O(nlogn)，但其证明过程比文献[5]的简单．2009年Tan给出了一些检测多边形是否可被边界单线搜索者搜索的充分条件[7]，利用这些条件检测多边形的可搜索性只需O(n)的时间和空间，但这些检测条件的证明过程相当复杂．

本文给出了一些检测多边形是否可被边界单线搜索者搜索的特征，这些特征类似于文献[6]中提出的，但采用不同的定义方式和证明方法将其时间复杂度从O(nlogn)降到O(n)．此时间复杂度是检测多边形的边界单线搜索性的下界，已不可能再优化．同时，这些特征由文中所构造的简化骨架V图论证，其证明过程比文献[7]的简洁．

1 基本概念与结果

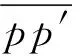
对于搜索者s和其光束点f以及任意边界点p，如果满足：s和f从p开始分别沿∂P逆时针和顺时针移动，在保持s和f相互可见的情况下，它们无法继续向前移动，则称p为死锁点．如图2中d即为一个死锁点．

设P为一个简单多边形，u和v为P中两个不同顶点，L和R分别表示∂P上从u到v的顺时针和逆时针边界链．如果L和R相互勉强可见，即L上每一点从R上某些点可见，反之亦然；则称P为关于点对(u,v)的LR可见多边形．

假设r∈P,q1,q2∈∂P3点共线，如果满足：①点q1从r可见；②边界∂Pcw(q1,q2]上的所有点从r都不可见；③每个包含q2的开区间，一定包含从r可见的另一点，则称(q1,q2)形成一个相对于r的左间隔边[9]，如图3．右间隔边定义类似．左右间隔边统称为间隔边．

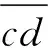
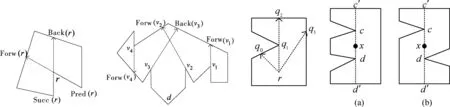
图1 反射点r形成的向前向后扩展点 图2 由反射点形成的(非)冗余组成 图3 相对于r的左间隔边 图4 (a)由c,d形成的同侧双切线(b)c,d形成的异侧双切线

从任意点开始，沿顺时针方向测量边界的总长度，记为|∂P|．对于任意实数x，总可以找到唯一的整数k，使得0≤x-k|∂P|≤|∂P|，因此x对应于边界∂P上的一点．

可视空间(简称V空间)记为V[8]，它包括射线y=x(开始线S)和y=x-|∂P|(目标线G)中间所夹的无限区域，如图5所示，图中D=|∂P|．

假设p=(a,b)∈V，q=(c,d)∈V，若b>d，则称p(q)在q(p)的北(南)边，类似地，若a>c，则称p(q)在q(p)的东(西)边[8]．

多边形的可视图(简称V图)[8]是在V空间中将部分区域用灰色表示且满足：一个点p(x,y)∈V是灰色的当且仅当x和y不能相互可见．

对于任意点p=(a,b)∈V，观察其关于射线y=x的对称点p′(b,a)，因为a与a-|∂P|在∂P上表示同一个点，且b与b+|∂P|在∂P上也表示同一个点，所以p=(a,b)∈V是灰色的当且仅当p1=(b,a-|∂P|)∈V和p2=(b+|∂P|,a)∈V也是灰色的．因此图5中p与p1、p2两点是对称的．特殊地，S上的点(a,a)与G上的点(a,a-|∂P|)和(a+|∂P|,a)也是对称的．

以下说明怎样将一个简单多边形用V图表示，多边形中的不可见区域都是由反射点造成的，因此在V图中只考虑反射点的信息，从而简化操作．首先在多边形边界∂P上标识出每个反射点v的向前扩展点Forw(v)和向后扩展点Back(v)；然后从任意一个边界点开始，对∂P上的所有反射点和每个反射点对应的向前与向后扩展点按顺时针排序；再在V图中按照它们在原多边形中的排序位置用坐标表示出来，V图中的原点对应排序的始点．

V图中每个反射点都可形成2个对称的灰色区域，此灰色区域称为障碍物[8]．与射线S相切的障碍物为东南(简写为SE)障碍物，与射线G相切的为西北(简写为NW)障碍物．如图6所示，反射点r对应一个东南障碍物SE(r)和一个西北障碍物NW(r)，SE(r)有2条线段，一条水平向右延长到Forw(r)(称为向东线)，一条垂直向下延长到Back(r)(称为向南线)．对应地，NW(r)也有2条线段，一条水平向左延长到|∂P|+Back(r)(称为向西线)，一条垂直向上延长到Forw(r)(称为向北线)．称这些线段为V图的骨架线段．

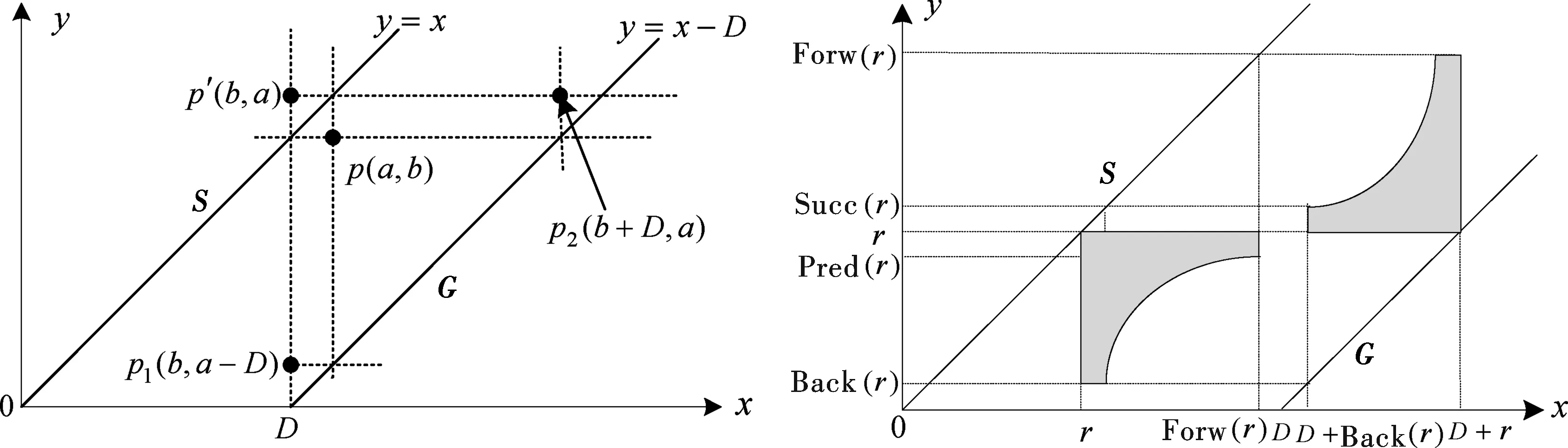
图5 可视空间 图6 由反射点r形成的SE和NW障碍物

由于可搜索多边形的主要信息都包含在V图中反射点所对应的骨架线段中，所以将V图中的每个反射点所对应的障碍物用两条骨架线段来代替，这样构造的图称为骨架V图[8]．图8为图7所对应的骨架V图，图7中的反射点1在V图中对应障碍物SE(1)和NW(1)，而在骨架V图中SE(1)对应一条向东骨架线段延长到Forw(1)和一条向南骨架线段延长到Back(1)．由对称性可知，NW(1)也同样对应两条骨架线段．其他反射点的情形类似．

为简化证明，在骨架V图中只表示多边形中有双切线的反射点的信息，忽略其他点的信息．若两反射点u,v具有同侧双切线，则表示为S(G)上u,v所对应的骨架线段相交；若两反射点u,v具有异侧双切线，则表示为S(G)上u对应的骨架线段与G(S)上v对应的骨架线段相交，这样构造的图称为简化骨架V图．图9为图7所对应的简化骨架V图．

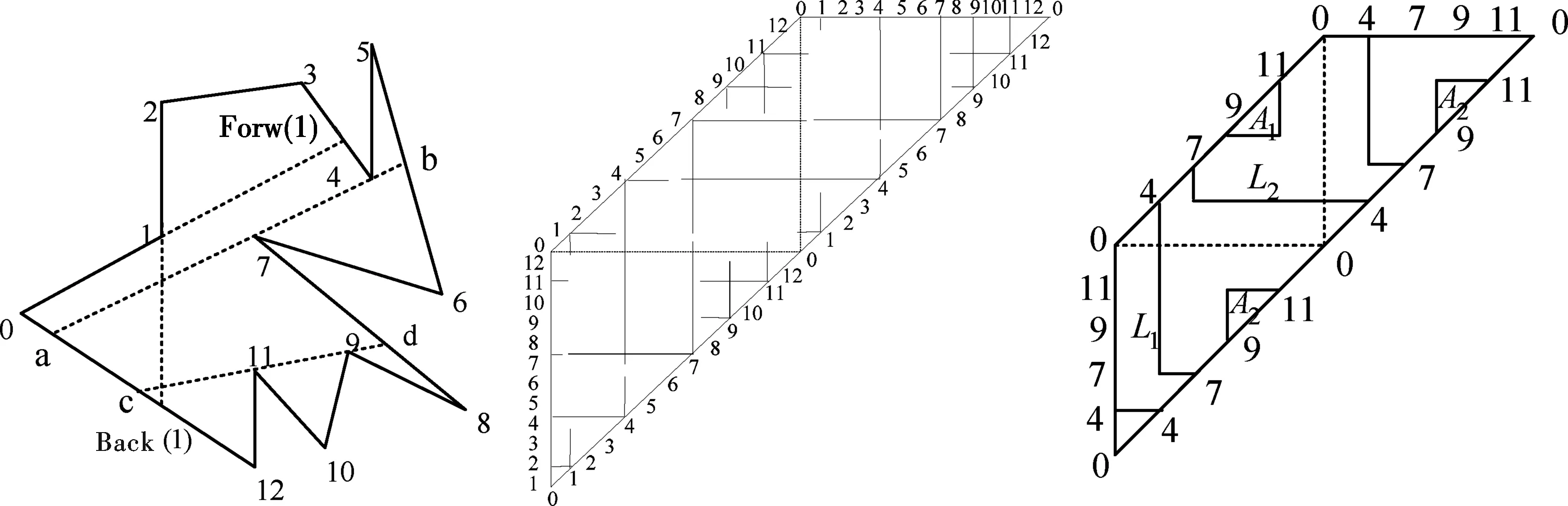
图7 简单多边形 图8 图7对应骨架V图 图9 图7对应简化骨架V图

在V图中，合法的搜索路径是从S上的一点开始顺着白色的区域可以到达G上的一点，并且可从右到左穿过障碍物．在骨架V图表示为可从右到左穿过垂直的骨架线段[4]．

定理1[4]一个给定的多边形可被一个边界单线搜索者搜索，当且仅当在其V图中存在一条合法的搜索路径．

定理2[4]一个给定的多边形可被一个边界单线搜索者搜索，当且仅当在其骨架V图中存在一条合法的搜索路径．

简化骨架V图是根据双切线和V图的关系简化而来的，故由定理1，2可得出如下结论．

定理3一个给定的多边形可被一个边界单线搜索者搜索，当且仅当在其简化骨架V图中存在一条合法的搜索路径．

简化骨架V图不但构造简单，而且在其中寻找一条合法搜索路径也很容易．以下给出了单线搜索多边形与LR可见多边形的关系和一些相关的定理．

定理4[1]若多边形P可被一个单线搜索者搜索，则P一定是LR可见多边形．

定理5[10]确定一个多边形是否为LR可见多边形只需O(n)的时间，并且可在O(n)的时间内计算出LR可见多边形中所有非冗余的组成．

定理6[11]判断所有的点x是否为死锁点只需O(n)的时间，由此可以确定多边形P是关于点对(x,y)的LR可见多边形．

2 检测多边形是否可搜索的特征

为叙述方便，先简述文献[6]中的一些概念，但方式略有不同．

定义1两个可见的反射点u,v有非冗余的逆时针(向前)组成，称u,v构成单右双切线．

定义2两个可见的反射点u,v有非冗余的顺时针(向后)组成，称u,v构成单左双切线．

定义3对于多边形中3个相互可见的反射点u,v,w(顺时针次序)和∂P上的一点p，若满足：①p,w∈P[v,Back(v)]；②p∉P[u,Back(u)]且p∉P[w,Back(w)]；③P[u,Back(u)]和P[w,Back(w)]是非冗余的，则称点p存在一条双右双切线．如图10．

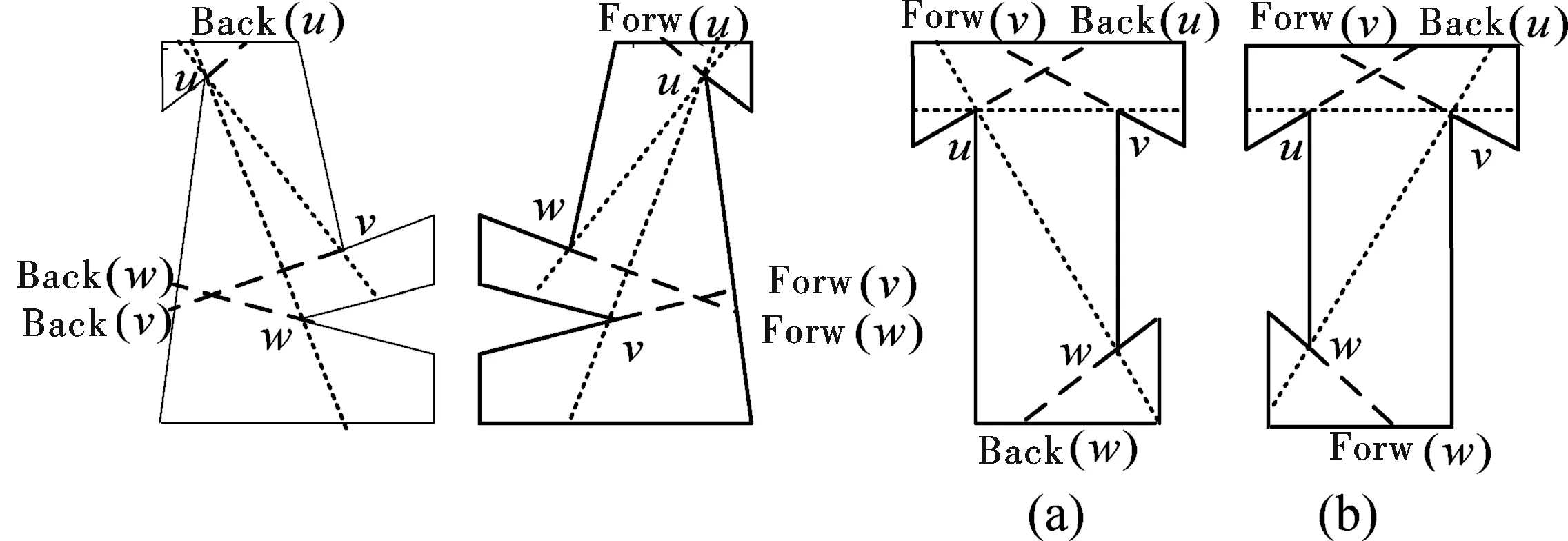
图10 双右双切线 图11 双左双切线 图12 特殊多边形

定义4对于多边形中3个相互可见的反射点u,v,w(顺时针次序)和∂P上的一点p，若满足：①p,v∈P[w,Forw(w)]；②p∉P[u,Forw(u)]且p∉P[v,Forw(v)]；③P[u,Forw(u)]和P[v,Forw(v)]是非冗余的，则称点p存在一条双左双切线．如图11．

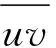
定理7一个多边形P不可被一个边界单线搜索者搜索，当且仅当P中存在以下某一情形：

(C1)多边形的每个边界点p都在一条同侧双切线的内侧．

(C2)多边形的每个边界点p都存在一条双右(左)双切线．

(C3)多边形的一些边界点在同侧双切线的内侧，其余的每个边界点都存在一条双右(左)双切线．

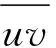
证(1)充分性．若P中存在(C1)～(C4)中的某一种情形，假定P中共切线的反射点有4个且满足条件(C1),其对应的简化骨架V图如13(a)所示，从图中可以看出不存在一条合法的搜索路径.P中若存在(C2)，(C3)或(C4)的情形，图13(b),(c)和(d)分别表示了P中有3个满足条件(C2)，有5个满足条件(C3)和3个满足条件(C4)的共切线的反射点所对应的简化骨架V图，3个图中都不存在一条合法的搜索路径.推广到P中有多个满足条件(C1)，(C2)，(C3)或(C4)的共切线的反射点的情形也相同.由定理3可知，P不可被一个边界单线搜索者搜索．

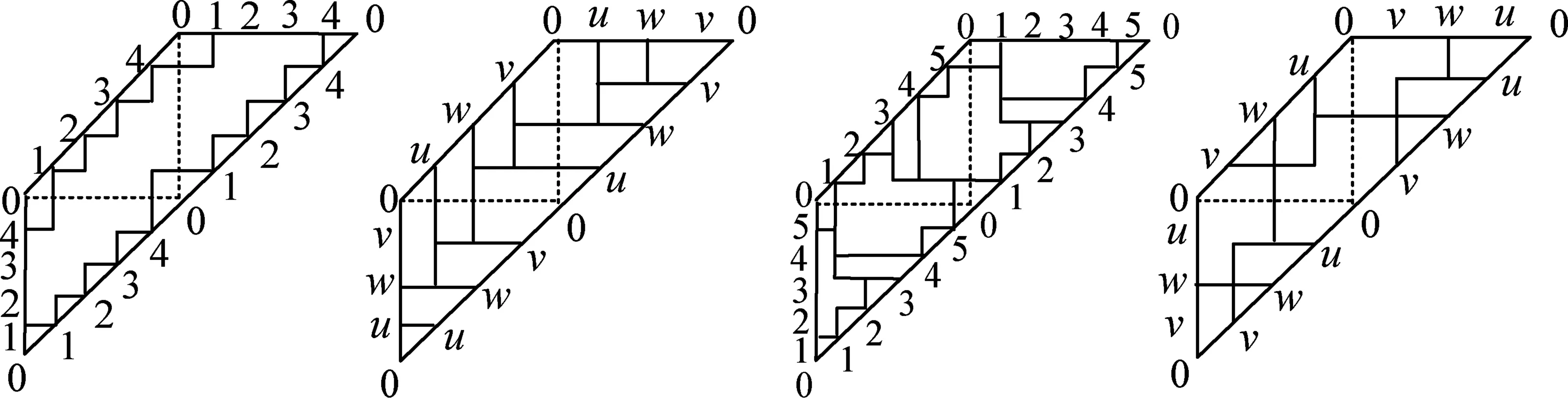
a b c d图13 多边形满足定理7中条件的简化骨架V图示例，分别为a.(C1);b.(C2);c.(C3);d.(C4)

(2)必要性．如果一个多边形P不可被边界单线搜索者搜索，由定理3可知，P对应的简化骨架V图中一定不存在一条合法的搜索路径，即简化骨架V图中出现以下情形：

1) 开始线S上的所有边界点都处于陷阱区域(搜索者进入此区域无法跳出，如图14(a)中S线上的u,v区域和图14(c)中S线上的w,v区域)，即不存在一点可以作为搜索的入点．这种情形只出现在P的边界点在同侧双切线的内侧或者存在一条双左双切线．

2) 目标线G上的所有的边界点都处于不可达区域(如图14(a)中G线上的u,v区域和图14(b)中G线上的w,v区域)，即不存在一点可以作为搜索的完成点．这种情形只出现在P的边界点在同侧双切线的内侧或者存在一条双右双切线．

3)S上有开始点，G上也有完成点，但从S上的所有入点都不可到达G上的某点，即出现(C4)所表示情形．

上述情形1)、2)对应条件(C1)，(C2)或(C3)，所以P不可被边界单线搜索者搜索，一定存在(C1)到(C4)中的某一种，且只存在这些情形．

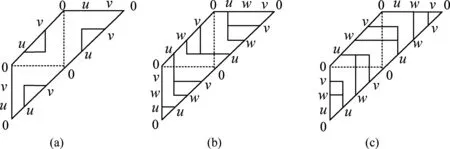
图14 (a)同侧双切线的简化骨架V图；(b)双右双切线的简化骨架V图；(c)双左双切线的简化骨架V图

定理8利用定理7检测一个给定的有n个顶点的多边形P是否可被一个边界单线搜索者搜索只需O(n)的时间和空间．

证首先检测多边形P是否为LR可见多边形，只需线性时间[10]，若P不是LR可见多边形，由定理4可知，P不可被一个单线搜索者搜索．若P是LR可见多边形，再用定理7检测．下面给出了如何在O(n)的时间和空间内验证定理7中特征的证明过程．

对于(C1)，由定理6可知，可在O(n)的时间内检测出所有的搜索入点p是否为死锁点，检测p是否死锁即检测p是否在一条同侧双切线的内侧，因此检测完所有的入点p是否都存在一条同侧双切线且p在其内侧也只需O(n)的时间．

对于(C2)，首先检测所有的非冗余的顺时针(逆时针)组成需O(n)的时间，再依次检测下列条件：①是否存在一个反射点w及任意一个边界点p在另一个反射点v的顺时针(逆时针)组成中，只需O(1)时间；②是否存在一个与v可见的反射点u，并且u,v构成非冗余的顺时针(逆时针)组成且不包括p，只需O(1)时间．即检测P的任意一个边界点p是否存在一条双右(左)双切线只需O(1)时间．所以检测完所有的边界点共需O(n)的时间．

对于(C3)，它是(C1)和(C2)的组合，检测多边形中的边界点是否为死锁点只需O(n)时间，然后再检测除死锁点之外的其余边界点是否都存在双右(左)双切线也只需O(n)时间，所以检测完多边形的所有边界点需O(n)时间．

对于(C4)，可以在检测边界点p是否死锁时外加一个限制条件，若检测到一个边界点p在由反射点u,v构成的同侧双切线的内侧，则再检测此双切线的内侧是否存在另一反射点w，使得w形成的顺时针(逆时针)组成与u(v)形成的顺时针(逆时针)组成构成非冗余的关系，这只需O(1)时间，因为所有的非冗余的顺时针(逆时针)组成都在O(n)的时间内已检测出．若存在这样的w，则断定此多边形不可被一个边界单线搜索者搜索；若本区域不存在这样的w，则继续在下一死锁区域用同样的方法检测．检测完所有的入点p是否为死锁点只需O(n)的时间[11]，所以(C4)的检测时间为O(n)．

综上所述，利用定理7检测一个多边形是否可被一个边界单线搜索者搜索只需O(n)的时间，并且由上述证明过程可以看出，定理7中特征的验证所需空间复杂度也为O(n)．

3 总结

本文给出了一些检测多边形是否可被一个边界单线搜索者搜索的特征，并利用本文构造的简化骨架V图进行证明，比文献[7]的证明简单，将文献[6]的时间复杂度从O(nlogn)降到O(n)．是否可将本文的证明方法应用到两个搜索者模型中，尚待进一步研究．

参考文献：

[1]SUZUKII,YAMASHITAM.Searchingforamobileintruderinapolygonalregion[J].SIAMJournalonComputing, 1992, 21(5): 863-888.

[2]PARKSM,LEEJH,CHWAKY.Acharacterizationoftheclassofpolygonssearchablebya1-searcher.TechnicalReportCS/TR-2000-160[R].Kaist:KoreaAdvancedInstituteofScienceandTechnology, 2000.

[3]TANX.Searchingasimplepolygonbyak-searcher[J].LectureNotesinComputerScience, 2000, 1969/2000:275-319.

[4]LAVALLESM,SIMOVB,SLUZKIG.Analgorithmforsearchingapolygonalregionwithaflashlight[J].InternationalJournalofComputationalGeometryandApplications, 2002, 12(1/2): 87-113.

[5]TANX.Acharacterizationofpolygonalregionssearchablefromtheboundary[J].LectureNotesinComputerScience, 2005, 3330/2005:200-215.

[6]KAMEDAT,ZHANGJZ,YAMASHITAM.Simplecharacterizationofpolygonssearchableby1-searcher:proceedingsofthe18thCanadianconferenceoncomputationalgeometry,Kingston,Canada, 2006[C].Kingston:[s.n.],2006.

[7]TANX.Searchingapolygonalregionbyaboundarysearcher[J].JournalofComputerScienceandTechnology, 2009, 24(3): 505-516.

[8]KAMEDAT,YAMASHITAM,SUZUKII.On-linepolygonsearchbyasix-stateboundary1-searcher[R].TechnicalReportCMPT-TR2003-07,Canada:SimonFraserUniversity, 2003.

[9]SIMOVB,LAVALLESM,SLUTZKIG.Acompletepursuit-evasionalgorithmfortwopursuersusingbeamdetection:proceedingsofIEEEinternationalconferenceonroboticsandautomation,WashingtonDC,USA, 2002[C].WashingtonDC:[s.n.],2002.

[10]DASG,HEFFERNANPJ,NARASIMHANG.LR-visibilityinpolygons[J].ComputationalGeometryTheoryandApplications, 1997, 7(1): 37-57.

[11]BHATTACHARYABK,MUKHOPADHYAYA,NARASIMHANG.Optimalalgorithmsfortwo-guardwalkabilityofsimplepolygons[C]//DEHNEF,SACKTR,TAMASSIAR.AlgorithmsandDataStructures, 7thInternationalWorkshop,WADS2001,LNCS2125.NewYork:Springer-Verlag, 2001, 438-449.