二次曲率引力场方程非球对称解

曹学静,许扬,陈贻汉

(湖北大学 物理学与电子技术学院,湖北 武汉 430062)

现代宇宙观测表明,宇宙中几乎所有旋涡星系的旋转曲线都趋于平坦[1],此观测事实与旋涡星系已有的发光物质的分布相矛盾；对引力透镜效应的观测发现,透镜星系中总的发光物质质量远小于观测所推算得到的质量[2].鉴于牛顿引力理论对这些宇宙观测事实无法解释的困难,有人提出在Einstein广义相对论引力作用量中加上时空曲率平方项来解释旋涡星系旋转曲线趋于平坦与引力透镜质量问题.文献[3]从引力规范理论角度提出了一含有曲率平方项的拉格朗日函数,给出了二次曲率引力场方程,文献[4-5]在弱场线性近似条件下,求得二次曲率引力场方程的静态球对称解,其中包含了两项Yukawa势,表明二次曲率引力场作用量中的曲率平方项在小范围对引力相互作用给出弱的修正.本文中在弱场线性近似条件下,首先将二次曲率引力场方程分解为3个二阶线性偏微分方程,通过这3个偏微分方程的解得到二次曲率引力场方程的一般引力推迟势解；然后利用球谐函数将二次曲率静态时空作多偶极矩展开,求得非球对称静态二次曲率引力场,讨论有质标量引力场和有质张量引力场对广义相对论的局域修正.

1 二次曲率引力场方程的推迟势解

(1)

考虑弱场,时空流形M的度规张量gμ v可写成 gμ v=ημ v+hμ v

(2)

式中ημ v为平坦时空的Mikowski度规,hμ v为小的扰动.按文献[5],方程(1)的弱场线性近似解为

(3)

(4)

的解,ψμ v和φ分别是场方程

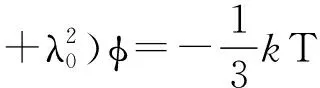
(5～6)

方程(4)～(6)的波动解分别为

(7)

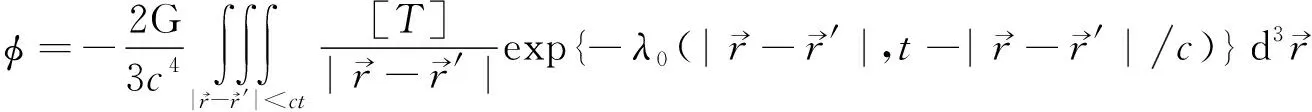
(8)

(9)

2 静态时空的球多偶极矩展开

对于静止松散的物质系统(压强p=0),方程(4)～(6)的解(7)～(9)式简化为

(10)

(11)

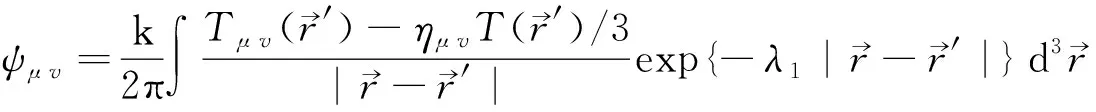
(12)

式中

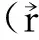
(13)

这里ρ(x)为物质系统的静止质量密度,uμ为四维速度.

(14)

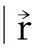
(15)

式中Il(x)和Kl(x)分别为l阶第一类和第二类虚宗量贝塞尔函数,脚指标i=0,1.

下面我们仅考虑物质系统外部的引力场.

将(13)和(14)式代入(10)式,我们有

(16)

其中

(17)

定义为Einstein引力场的多偶极矩.

同理,将(13)和(15)式代入(11)式,有质标量场可写成

(18)

类似地,(13)和(15)式代入(12),可将有质张量场写成

(19)

其中

(20)

(21)

利用(16)、(18)和(19)式,将(21)式引力势写成球谐函数的展开形式

(22)

虚宗量贝塞尔函数Kl(x)为单调衰减函数,x→∞时,Kl(x)→0.因此,当参数λ0和λ1趋于无穷,或r→∞,(22)式简化为

(23)

此为牛顿引力势的多极矩展开表达式.

3 结论

参考文献:

[1] Faber S M, Gallagher J S.Masses and mass-to-light ratios of galaxies[J].Ann Rev Astron. Astrophys,1979,17:135-187.

[2] Dar A. Tests of general relativity and Newtonian gravity at large distances and the dark matter problem[J]. Nucl Phys B Proc Suppl,1992,B28:321-326.

[3] 陈贻汉,邵丹,邵亮,等.引力的曲率平方理论[J].数学物理学报,2002,22A(4):477-481.

[4] 肖明,龙芸,邓永菊.曲率平方引力场方程的静态轴对称解[J].湖北大学学报:自然科学版,2008,30(3):257-259.

[5] Chen Yi han, Shao Chang gui. Precession of orbiting gyroscope in higher-order gravitational field caused by rotating body[J].Intern J of Theor Phys,2002,41(7):1377-1387.