半素PI-环的正则元

游松发

(湖北大学 数学与计算机科学学院,湖北 武汉 430062)

本文中环R是不必有单位元的结合环,半素环是没有非零幂零理想的环.

令A是R的子集,定义lR(A)={r∈R|rA=0},rR(A)={r∈R|Ar=0},分别称为A在R中的左和右零化子.特别地,若lR(a)=0,则称a是R的左正则元;rR(a)=0,则称a是R的右则元;若a既是R的左正则元,又是R的右正则元,则称a是R的正则元.

对半素环R,若IΔR,令J=lR(I)⟹JI=0⟹(IJ)2=0⟹IJ=0⟹J⊆rR(I),即lR(I)⊆rR(I),我们有lR(I)=rR(I),此时也记它们为AnnR(I).

设E是R的左(右)理想,若对R的任一非零左(右)理想I,有E∩I≠0,则称E在R中是本质的.定义Sl(R)={a∈R|lR(a)在R中是本质的},Sr(R)={a∈R|rR(a)在R中是本质的},易证Sl(R)和Sr(R)都是R的理想,分别称为R的左、右奇异理想.

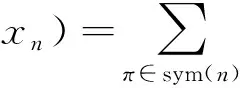
引理1 若a是环R的左正则元,且Ra是PI的,则Ra包含R的一个非零理想.

引理1的证明假设在R的所有形如Rai的左理想中,Rak所满足的多项式恒等式的次数最低,不失一般性,假设所满足的多项式恒等式是多重线性的,且其有形式

f(x1,…,xn)=f1(x1,…,xn-1)xn+f2(x1,…,xn).

其中,f1的次数比f的次数低,f2的所有单项中最后一个未定元都不是xn,令xj=rja2k(j=1,…,n-1),xn=rnak(r1,…,rn∈R)，代入f我们有

f1(r1a2k,…,rn-1a2k)rnak+f2(r1a2k,…,rn-1a2k,rnak)=0，

即f1(r1a2k,…,rn-1a2k)rnak=-f2(r1a2k,…,rn-1a2k,rnak)∈Ra2k,

又因a是左正则元,lR(a)=0所以f1(r1a2k,…,rn-1a2k)rn∈Rak,故f1(r1a2k,…,rn-1a2k)R⊆Rak,从而Rf1(r1a2k,…,rn-1a2k)R⊆Rak⊆Ra.

另一方面,由于Ra2k⊆Rak,所以Ra2k满足f1(x1,…,xn)=0,又据Rai中Rak的选取,Rak不满足f1(x1,…,xn-1)=0,因而一定存在r1,…,rn-1∈R,使f1(r1a2k,…,rn-1a2k)≠0,故有Rf1(r1a2k,…,rn-1a2k)R≠0,即Ra包含R的一个非零理想Rf1(r1a2k,…,rn-1a2k)R.

引理2 若a是半素PI-环R的左正则元,则Ra包含零化子为0的一个非零理想.

引理2的证明考察含于Ra的R的所有理想之和I,须证:AnnR(I)=0.

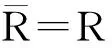
定理3 若a是半素PI-环R的左正则元,则a是R的右正则元,且Ra是R的一个本质左理想.

定理3的证明令I是引理2中含于Ra的R的所有理想之和,∀x∈R,若ax=0,则Rax=0,从而Ix=0,由引理2,x=0,即rR(a)=0.

另一方面,若L是R的任一非零左理想,则0≠IL⊆I∩L⊆Ra∩L,即Ra是R的一个本质左理想.

注PI-环的左正则元不一定是右正则的;PI-环的左正则元a生成的右理想aR不一定是本质右理想.

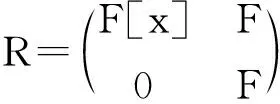
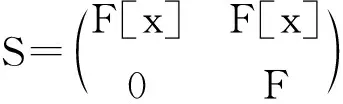
推论4 若x,y是有1的半素PI-环R中任意两个元,且xy=1,则yx=1.

推论4的证明由xy=1可知lR(x)=0,由定理3,有rR(x)=0.

又x(1-yx)=x-xyx=x-x=0,所以1-yx∈rR(x)=0,因此yx=1.

定理5 若a是半素PI-环R的左正则元,则R与Ra满足相同的多项式恒等式.

定理5的证明由R半素PI,可知∩{Pα|Pα是R的素理想}=0.由引理2,存在含于Ra的理想I,使AnnR(I)=0.由于所有素理想的交为0,因而存在某素理想Pβ,使I⊄Pβ,将R的所有素理想分为两部分,一部分包含I,它们的交记为A,另一部分不包含I,它们的交记为B.对于半素环,由于A∩B=0⟺AB=0,因此B可将A零化,再据AnnR(I)=0.可知B=0,即0=∩{Pγ|Pγ是素理想,且I⊄Pγ},考察Rγ=R/Pγ,Rγ是素的,且有一个非零理想(I+Pγ)/Pγ是PI的,据文献[2]，Rγ与(I+Pγ)/Pγ,满足相同的恒等式,而R是Pγ的亚直和,R与Pγ满足同样的多项式恒等式[1],故R满足I的多项式恒等式,从而R与Ra满足相同的多项式恒等式.

引理6(Rowen)[1,Th1.6.27]若R是半素PI-环,I是R的任一非零理想,Z(R)是R的中心,则I∩Z(R)≠0.

引理7 若R是半素PI-环,则Sr(R)=Sr(R)=0.

引理7的证明先证对于R的本质左理想E,有lR(E)=0.事实上,若J=lR(E)≠0,则JE=0,且J∩E≠0,但(J∩E)2=(J∩E)(J∩E)⊆JE=0⟹J∩E=0,这是矛盾的.

若Sl(R)≠0,由引理6,Sl(R)∩Z(R)≠0,选取0≠λ∈Sl(R)∩Z(R),由λ∈Sl(R)可知,必存在R的本质左理想E,使Eλ=0,而λ∈Z(R),所以λE=0,即有0≠λ∈lR(E)=0,这是矛盾的,因而Sl(R)=0,同理有Sr(R)=0.

定理8 若R是半素PI-环,则R有一个唯一的最大左商环Q满足:

(1)有1的Q是Neumann-正则的,且Sl(Q)=0;

(2)R的每一正则元在有1的Q中是可逆的.

定理8的证明(1)因Sl(R)=0,直接由文献[3]的主要结果可知,R有一个唯一的最大左商环Q,在Q有1的情形下,Q是Neumann-正则的,且Sl(Q)=0.

(2)若a是R的正则元,则lR(a)=0,因而lQ(a)=0,由于Q是Neumann-正则的,因而存在b∈Q,使a=aba,故1-ab∈lQ(a)=0,即ab=1,同推论4,因lQ(1-ba)⊇Ra,且Ra是本质的,因此1-ab∈Sl(Q)=0,我们同时有ab=1且ba=1,即a在Q中是可逆的.

参考文献:

[1] Rowen L H.Polynomial identities in ring theory[M].New York: Academic Press,1980.

[2] Amitsur S A.Prime rings satisfying polynomial identities with arbitrary coefficients[J].Proc London Math Soc,1967,17(3):470-486.

[3] Johnson R E.Quotient rings of rings with zero singular ideal[J].Pacific J Math,1961,11:1385-1392.

[4] Zheng Yumei, You Songfa.A note on radicals in hypercentral extensions of rings[J].SEA Bull Math,1993,17(1):105-108.

[5] You Songfa.The primitivity of extended centroid extension on prime GPI-rings[J].Advances in Math,2000,29(4):331-336.

[6] You Songfa.The essential(one-sided) ideal of semiprime PI-rings[J].Acta Math Sinica,2001,44(4):747-752.

[7] You Songfa.Eulerian graphs and polynomials identities on matrix rings[J].Advances in Math,2003,32(4):425-428.