运用3种判据推导热力学系统平衡稳定性条件

肖波齐， 林紫霞， 蒋国平

(1.三明学院物理与机电工程系，福建三明 365004;2.广州大学工程抗震中心，广东广州 510405)

运用3种判据推导热力学系统平衡稳定性条件

肖波齐1， 林紫霞1， 蒋国平2

(1.三明学院物理与机电工程系，福建三明 365004;2.广州大学工程抗震中心，广东广州 510405)

根据正定、负定二项式性质及雅可比行列式的性质，分别利用熵判据、吉布斯判据、自由能判据对热力学系统平衡稳定性条件进行了详细推导，均能得出系统处于平衡稳定性状态所满足的条件.

热力学系统； 判据； 平衡稳定性条件

系统从非平衡态向平衡态的变化过程中，系统的状态参量必发生变化，最终达到极大值或极小值,在不同的条件下可得到不同的平衡判据.如对孤立系统，平衡态的S最大，即δS=0及δ2Slt;0；在F、V不变的条件下，平衡态的T最小，即有δT=0及δ2Tgt;0；在G、P不变的条件下，平衡态的T最小，即有δT=0及δ2Tgt;0；在U、S不变的条件下，平衡态的V最小，即有δV=0及δ2Vgt;0；在F、T不变的条件下，平衡态的V最小，即有δV=0及δ2Vgt;0等.对于不同的热力学系统，根据系统中宏观量的条件不同，可以采用不同的热力学平衡判据，从而得到系统的平衡条件.在不同的条件下系统有不同的平衡判据和平衡的稳定性判据，根据系统实际所处的条件，利用相应的平衡判据和平衡的稳定性判据，可得到系统的平衡条件和平衡的稳定性条件，从而可以分析某一个理论过程是否真实存在.用热力学系统的平衡判据推导孤立系统平衡的稳定性条件，利用平衡的稳定性条件可以判断这个系统是否处于稳定平衡状态.熵是从热力学第二定律引出来的一个重要的概念，应用熵判据可以求得系统的平衡条件及平衡的稳定性条件，同时利用吉布斯判据与自由能判据推导热力学系统的平衡稳定性条件也可以得到同样的结果.

1 应用熵判据推导系统的平衡稳定性条件

熵增加原理是热力学第二定律的数学表述.熵增加原理指出，孤立系统的熵永不减少.孤立系统中发生的任何不可逆过程，包括趋向平衡的过程，都是朝着使系统的熵增加的方向进行的.因此，如果—个孤立系统达到了熵为极大的状态，系统就达到了平衡状态.我们可以利用熵函数的这个性质来判定孤立系统的平衡状态.这称为熵判据.要找出熵的极大，可以设想系统发生各种可能的虚变动，而比较由此引起的系统的嫡的改变.在求各种可能的虚变动所引起的熵的改变时，系统在变动中的外加约束条件(孤立系条件)需要用函数的形式表示.孤立系统是完全隔绝的，与其他物体既没有热量的交换，也没有功的交换.如果只有体积变化的功，孤立系条件相当于体积不变和内能不变.因此熵判据可以表达为：一个系统在体积和内能不变的情形，对于各种可能的虚变动，平衡态的熵最大.在数学上相当于在保持体积和内能不变的条件下通过对熵函数求微分而求极大.根据数学上熟知的结果，当熵函数的一阶微分等于零时，熵函数有极值；当熵函数的一阶微分等于零，二阶微分小于零时，熵函数有极大值.如果熵函数有几个可能的极大，则其中最大的极大相应于稳定平衡，其它较小的极大相应于亚稳平衡.亚稳平衡是这样一种平衡：对于无穷小的变动是稳定的，对于有限大的变动是不稳定的.如果对于某些变动，熵函数的数值不变，这相当于中性平衡.熵判据是基本的平衡判据.它虽然只适用于孤立系统，但只要把参与变化的全部物体都包括在系统之内，原则上可以对各种热动平衡问题作出回答.不过在实际应用上，对于某些经常遇到的物理条件引入其它判据是更为方便的.对于孤立系统，从非平衡态向平衡态过渡，是一种由不均匀向均匀的变化过程,为不可逆过程，满足熵的增加原理.对于一个微元过程，有dS≥0，系统从非平衡态向平衡态过渡，系统的熵值将增加.达到平衡态时，系统的宏观过程终止，说明系统的熵达到极大值.反之，如果孤立系统已经达到了熵为极大值的状态，就不可能再发生任何宏观变化,即处于平衡状态.利用熵函数这一性质来判定孤立系统的平衡态，称为熵判据[1-3].以下进行详细推导：设V1、V2、U1、U2、N1、N2分别代表系统两部分的体积、内能和粒子数[4].令:S1=(U1,V1,N1),S2=(U2,V2,N2),在平衡态附近若有一虚变动，因在平衡态时熵有极大值，得：

δS=δS1+δS2=0,δ2S=δ2S1+δ2S2lt;0，

(1)

其中δS=0为平衡的必要条件；δ2Slt;0为平衡的稳定性条件.此即为热力学系统平衡态的熵判据.但在实际应用中,引入其它平衡判据后应用会更方便(如后面所讨论的吉布斯判据和自由能判据).由式(1)得到系统的平衡条件为：

T1=T2(热平衡条件)；P1=P2(力学平衡条件)；

μ1=μ2(相变平衡条件).

(2)

根据微分的性质，熵的二阶微分为：

(3)

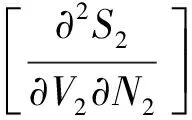
(4)

由热力学基本微分方程得：

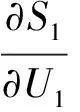
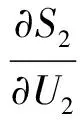
(5)

将式(5)代入式(3)、(4)得：

(6)

(7)

将U1=N1u1及V1=V1v1；U2=N2u2及V2=N2v2代入式(6)、(7)得：

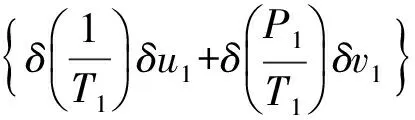
(8)

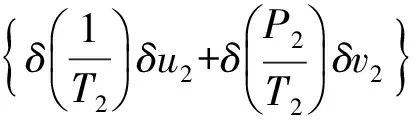
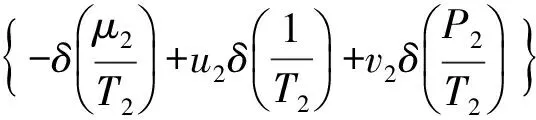
(9)

式(8)、(9)化简得：

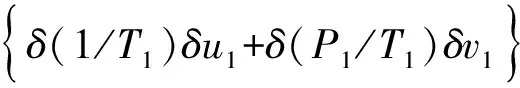
(10)

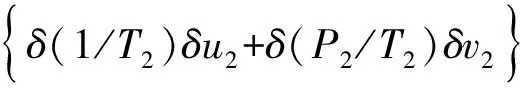
(11)

由于N1和N2均是正数，且两相平衡时与N1、N2的大小无关，要满足上式必有：

δ(1/T1)δu1+δ(P1/T1)δv1lt;0,

δ(1/T2)δu2+δ(P2/T2)δv2lt;0.

(12)

由式(12)知如果系统达到稳定平衡，每一部分都须满足：

δ(1/T)δu+δ(P/T)δvlt;0.

(13)

由上面的热力学基本微分方程得：

(∂S/∂u)=1/T，(∂S/∂v)=P/T.

(14)

所以式(13)化为平方和的形式为：

由于u、v可以任意变化，要使上式成立必须同时满足：

(15)

将式(14)代入式(15)得：

(∂2S/∂u2)=[∂(1/T)/∂u]=-(∂T/∂u)/T2.

(16)

把热力学微分方程∂u/∂T=Cv代入式(16)得：

结合式(15)得：

Cvgt;0,(∂2S/∂v2)(∂2S/∂u2)-(∂2S/(∂v∂u))2gt;0.

(17)

用矩阵表示上式，运用雅科比行列式性质得：

结合式(17)得：(∂P/∂V)Tlt;0.

由(∂P/∂V)Tlt;0与式(17)可知，要使δ2S对于各种可能的虚变动都小于零，必须满足

Cvgt;0,(∂P/∂V)Tlt;0.

(18)

只有满足式(18)，系统才能处于平衡稳定性条件.

2 应用吉布斯判据推导系统的平衡稳定性条件

从熵判据的推导过程可以看出比较复杂，在实际应用上，对于某些经常遇到的物理条件引入其他判据时更为方便.以下对孤立系统在等温等压条件下，处于平衡稳定性状态需满足何种条件进行推导.在推导方法上，将利用雅科比行列式的性质及正定、负定二项式性质，使推导过程更简练[5-6].根据吉布斯函数公式：G1=U1+PV1-TS1得

δG1=δU1+PδV1-TδS1.

(19)

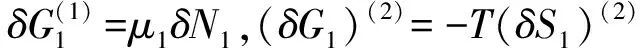
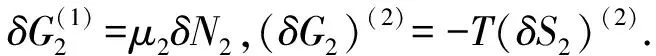
(20)

当(δG)(1)=0时，可得出平衡条件，由式(20)得：

(δG)(1)= (δG1)(1)+(δG2)(2)=

μ1δN1+μ2δN2=0.

(21)

因为总粒子数保持不变，所以δN1=-δN2，代入式(21)得：μ1=μ2，即孤立系统在等温等压条件下，处于平衡状态时，只需满足μ1=μ2(相平衡条件)，系统处于稳定平衡状态时，吉布斯函数虚变化的二级小量δ2G大于零.由式(20)得：

δ2G=(δG1)(2)+(δG2)(2)=

-T[(δS1)(2)+(δS2)(2)]gt;0.

(22)

对于等温、等压系统，有dG≤0，说明系统从非平衡态向平衡态的变化过程中，系统的吉布斯函数减小.当系统达到平衡态时，系统的过程终止，系统的吉布斯函数达到极小值.

反之，如果孤立系统已经达到了吉布斯函数为极小值的状态，就不可能再发生任何宏观变化，即处于平衡状态.这就是说，经等温等压过程后，吉布斯函数永不增加.在等温等压条件下，系统中发生的不可逆过程，包括趋向平衡的过程，总是朝着吉布斯函数减少的方向进行的.因此，处在等温等压条件之下的系统，如果达到了吉布斯函数为极小的状态，系统就达到了平衡状态.利用古布斯函数的这个性质来判定等温等压系统的平衡状态，称为吉布斯函数判据.在数学上这相当于在保持温度和压力不变的条件下通过对吉布斯函数求微分而求极小.类似地，这里也可能出现稳定平衡、亚稳平衡和中性平衡等不同的情况.

根据系统处于平衡态时吉布斯函数取极小值的条件，当系统处于平衡态时，若有一微小的虚变动，必有：δG=0及δ2Ggt;0，其中，δG=0为平衡的必要条件；δ2Ggt;0为平衡的稳定性条件.因为T大于零，所以由式(22)得：(δS1)(2)+(δS2)(2)lt;0，即

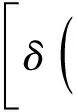
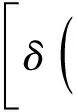
由于N1、N2都是正数，且两相平衡时，与N1、N2的大小无关，所以系统要处于稳定平衡时，要求系统中的每一部分都必须满足：

δ(1/T)δu+δ(p/T)δvlt;0.

(23)

根据热力学基本微分方程

(∂S/∂u)v=1/T，(∂S/∂v)u=P/T,

式(23)可化为：

(∂2S/∂u2)v(δu)2+(∂2S/∂v2)u(δv)2+

2[∂2S/(∂u∂v)]δuδvlt;0.

(24)

根据正定、负定二次型的性质，要满足式(24)，须有：

(25)

结合热力学基本微分方程与式(25)得：

(∂2S/∂u2)v=-1/(T2Cv)lt;0，

所以：Cvgt;0

根据雅科比行列式的性质及热力学基本微分方程式，结合式(25)，得：

因为等温等压条件下，压强和温度都是常数，所以上式微分的结果为零.所以，孤立系统在等温等压条件下，处于平衡稳定状态只需满足条件：Cvgt;0.

3 应用自由能判据推导系统的平衡稳定性条件

对于推导封闭系统在等温等容过程中处于平衡稳定性状态需满足的条件，利用自由能判据进行推导，更加方便[4，7].在推导方法上也是利用雅科比行列式的性质及正定、负定二项式性质进行推导，以下进行详细推导.因为自由能定义为F=U-TS,所以

δF=δU-TδS.

(26)

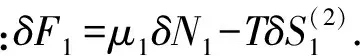
δF1(1)=μ1δN1，(δF1)(2)=-T(δS1)(2)；

δF2(1)=μ2δN2，(δF2)(2)=-T(δS2)(2).

(27)

当(δF)(1)=0时，由式(27)得：(δF1)(1)=μ1δN1+μ2δN2=0，因为δN1=-δN2，所以μ1=μ2.即孤立系统在等温等容条件下，处于平衡状态时，只需满足μ1=μ2.系统处于稳定平衡状态时，δ2F大于零.由式(27)得：

δ2F=-T[(δS1)(2)+(δS2)(2)]gt;0.

(28)

对于等温、无外功系统，有dF≤0，说明系统从非平衡态向平衡态的变化过程中，系统的自由能减小.当系统达到平衡态时，系统的宏观过程终止，系统的自由能达到极小值.反之，如果孤立系统已经达到了自由能为极小值的状态，就不可能再发生任何宏观变化，即处于平衡状态.这就是说，在等温等容过程中，系统的自由能永不增加.在等温等容条件下，系统中发生的不可逆过程，包括趋向平衡的过程，总是朝着自由能减少的方向进行的.因此，处在等温等容条件下的系统如果达到了自由能为极小的状态，系统就达到了平衡状态.我们可以利用自由能函数的这个性质来判定等温等容系统的平衡状态.自由能判据：一系统在温度和体积不变的情形下，对于各种可能的变动，平衡态的自由能最小.在数学上这相当于在保持温度和体积不变的条件下.通过对自由能函数求微分而求极小.与熵判据中的情形相似，这里也可能出现稳定平衡、亚稳平衡和中性平衡等不同的情况.

根据系统处于平衡态时自由能取极小值的条件，当系统处于平衡态时,若有一微小的虚变动，必有：δF=0及δ2Fgt;0，其中,δF=0为平衡的必要条件；δ2Fgt;0为平衡的稳定性条件.因为T大于零，所以由式(28)得：(δS1)(2)+(δS2)(2)lt;0，即

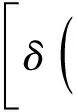
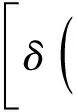
由于N1、N2都是正数，且两相平衡时，与N1、N2的大小无关，所以系统要处于稳定平衡时，要求系统中的每一部分都必须满足

δ(1/T)δu+δ(P/T)δvlt;0.

(29)

根据热力学基本微分方程

(∂S/∂u)v=1/T,(∂S/∂v)u=P/T，

式(29)可化为：

(∂2S/∂u2)v(δu2)+(∂2S/∂v2)u(δv)2+

2[∂2S/(∂u∂v)]δuδvlt;0.

(30)

根据正定、负定二次型的性质，要满足式(30)，须有式(25)成立.结合热力学基本微分方程与式(25)得：(∂2S/∂u2)v=-1/(T2Cv)lt;0.因为T2gt;0，所以Cvgt;0.

根据雅科比行列式的性质及热力学基本微分方程，结合式(25)得：

结合Cvgt;0，得(∂P/∂v)Tlt;0.所以，孤立系统在等温等容条件下，处于平衡稳定状态的条件为Cvgt;0，(∂P/∂v)Tlt;0.

4 分析和结论

通过以上讨论、分析可见，如果一个孤立系统达到了熵为极大的状态，系统就达到了平衡状态.我们可以利用熵函数的这个性质来判定孤立系统的平衡状态.在等温等压条件下，系统的吉布斯函数永不增加.我们可以利用吉布斯函数的这个性质来判定等温等压系统的平衡状态.在等温等容过程中，系统的自由能永不增加.我们可以利用自由能函数的这个性质来判定等温等容系统的平衡状态.当系统处于稳态平衡时，除满足式(2)外，还必须满足平衡的稳定性条件：Cvgt;0，(∂P/∂v)Tlt;0.否则平衡将为不稳定的状态.即此状态将很难维持，因此，对于实际系统就可以直接用以上条件来判定某一过程的各个状态是否存在.假设系统的温度由于涨落而略高于外界，热量将从系统传递到外界.如果系统满足条件Cvgt;0，热量的传递将使系统温度降低，从而恢复平衡.假如系统的体积由于涨落而发生收缩，如果系统满足(∂P/∂v)Tlt;0，系统的压力将增加而大于外界的压力，于是系统膨胀而恢复平衡.

本文利用正定、负定二项式及雅可比行列式的性质，对热力学系统平衡稳定性条件进行推导.利用熵判据、吉布斯判据、自由能判据均能推导出系统的平衡稳定性条件，而一般的书籍或论文所做的推导又主要是利用熵判据，本文采用3种判据进行推导，得出系统处于平衡稳定性状态所满足的条件.熵判据推导出来的结果是最普遍的，包括了热平衡条件、力学平衡条件与相平衡条件.不过在实际应用上，对于某些经常遇到的物理条件引入其他判据时更为方便.在满足相平衡的条件下，实际上已经满足了热平衡与力学平衡条件.在实际推导中，引入吉布斯判据或自由能判据求解系统处于平衡稳定性状态所满足的条件更简易.

[1] 汪志诚.热力学.统计物理[M].北京:高等教育出版社,1993:107-111.

[2] 钟云霄.热力学与统计物理[M].北京：科学出版社.1988:49-55.

[3] 马本堃,高尚惠,孙煜.热力学与统计物理学[M].北京：人民教育出版社，1994:90-95.

[4] 刘惠民,田强.固体物理学中平衡态的热力学条件分析[J].大学物理,2005,24(6):14-15.

LIU Huimin,TIAN Qiang. The analysis of thermodynamic equilibrium conditions in solid state physics[J]. College Physics, 2005,24(6):14-15.

[5] 贾世忠.论Gibbs方程的热力学本性及热力学函数的物理意义[J].大学物理, 2004,23(1):12-15.

JIA Shizhong. On the thermodynamics nature of the Gibbs equations and the physical meaning of the thermodynamic functions[J]. College Physics, 2004,23(1):12-15.

[6] 李鹤龄.Gibbs方程是否适用于开放系统[J].大学物理,2005,24(3):22-24.

LI Heling. Gibbs equations are also applicable to open system[J]. College Physics, 2005,24(3):22-24.

[7] 郭平生,韩光泽,华贲.能量公设与自由能判据的普遍化形式[J].大学物理,2005,24(9):38-41.

GUO Pingsheng, HAN Guangze, HUA Ben. The energy postulate and general form of the free energy criterion[J]. College Physics, 2005,24(9):38-41.

Keywords： thermodynamic system； criterion； stability condition of equilibrium

【责任编辑 庄晓琼】

STABILITYCONDITIONSOFEQUILIBRIUMFORTHERMODYNAMICSYSTEMDERIVEDFROMTHREECRITERIA

XIAO Boqi1， LIN Zixia1， JIANG Guoping2

(1. Department of Physics and Electromechanical Engineering, Sanming University, Sanming, Fujiang 365004, China;2. Earthquake Engineering Research Test Center, Guangzhou University, Guangzhou 510405, China)

According to the binomial formula of positive definite, negative definite and Jacobian determinant, the stability conditions of equilibrium for thermodynamic system are deduced in detail by using the entropy criterion, the Gibbs criterion and the free energy criterion.

2009-06-04

福建省省属高校科研专项基金资助项目(JK2009039)；福建省教育厅科技项目(JA07167);三明学院服务海西建设重点工程资助项目(HX200804);三明学院2009年教学改革资助项目(L0910/Q)

肖波齐(1980—)，男，湖北孝感人，三明学院讲师，主要研究方向：热力学统计物理教学和非线性科学及纳米流体性质，Email:xiaoboqi2006@126.com.

1000-5463(2010)01-0047-05

O414.1； O414.2

A