Laplace-Stieltjes变换的收敛性与增长性
2010-11-25孙道椿
罗 茜, 孙道椿
(1.嘉应学院数学学院, 广东梅州 514015; 2. 华南师范大学数学科学学院, 广东广州 510631)
Laplace-Stieltjes变换的收敛性与增长性
罗 茜1, 孙道椿2
(1.嘉应学院数学学院, 广东梅州 514015; 2. 华南师范大学数学科学学院, 广东广州 510631)
通过引进新的定义方式,得到了描述Laplace-Stieltjes变换的收敛性的3种收敛横坐标的公式,进而又讨论了增长性,得到了与最大模的增长级一样的新函数.
Laplace-Stieltjes变换; 收敛横坐标; 增长性
余家荣在文献[1]中结合 VALIRON[2]和KNOPP[3]中的方法,将幂级数的Cauchy-Hadamard 公式推广到Laplace-Stieltjes 变换,得到的结果均是不等式的形式. 在文献[4],又得到了关于二重Dirichlet级数和二重Laplace-Stieltjes 变换的相应结果.这些Laplace-Stieltjes变换的结果均依赖于预先取定的一个递增趋于无穷的且满足一定条件的序列{n},这样就可以将问题转化为类似于Dirichlet级数[5-7]的研究. 我们从另一个角度出发,改变以前依赖序列{n}来研究的状况,而试图得到一些新的较为广泛的结果.
1 主要定义


定义3F(s)的最大模为
定义4F(s)的增长级为
其中
2 有关收敛性的结果
首先得到一个与Dirichlet级数完全类似的结果[5].
引理1 如果F(s)在点s0=σ0+it0处收敛,那么

2)F(s)在σgt;σ0内收敛.







这时取ugt;M,xgt;u,则有




因此F(s)在Er上一致收敛. 由1),我们很容易得到2).






K(σ0)e-x(σ0-A)/2,
其中当σ0lt;0时,K(σ0)=2e-Kσ0;当σ0≥0时,K(σ0)=1. 因此











进一步,


对于一致收敛横坐标,我们也有如下结果.
引理2 如果F(s)在直线σ=σ0上一致收敛, 则F(s)在右半平面σ≥σ0上一致收敛.
定理2

K是一个正常数.
引理3 如果F(s)在点s=σ0处绝对收敛, 那么F(s)在σ≥σ0上绝对收敛.


3 有关增长性的一些结果


下面讨论Mu(σ,F)与μK(σ,F)的关系.
定理4 对上述的F(s),∀εgt;0,当σlt;0时,有下列不等式成立:


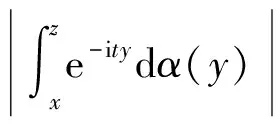


2eσxMu(σ,F)lt;2Mu(σ,F).
因此,μK(σ,F)≤2Mu(σ,F). 另一方面,


于是,当σlt;0时,对任意的εgt;0,




2μK(σ-ε,F)emK(σ-ε)e-σx≤

此时,若μK(σ,F)的增长级定义为
由定理4,立即可得如下推论.
推论1 对上述的F(s),有u=μK.
推论2 对上述的F(s),对任意的K1,K2gt;0,有μK1=μK2.
[1] 余家荣.Laplace-Stieltjes变换所定义的整函数之Borel线[J]. 数学学报,1963(3):471-484.
[2] VALION G.Entire functions and Borel’s directions[J].Proc Nat Acad Sci,1934,20:211-215.
[3] KNOPP K.Über die Konvergenzabscisse des Laplace-Integrals [J].Math Zeits,1951,54:291-296.
[4] 余家荣.二重Dirichlet级数和二重Laplace-Stieltjes变换的收敛性[J].武汉大学学报:自然科学版,1962(1):1-17.
[5] 余家荣.狄里克莱级数与随机狄里克莱级数[M].北京:科学出版社,1997.
[6] 孙道椿.Dirichlet级数的的级[J]. 华南师范大学学报:自然科学版,2001(3):14-19;77.
SUN Daochun. The order of Dirichlet series[J].Journal of South China Normal University:Natural Science Edition,2001(3):14-19;77.
[7] 黄志波,孙道椿. 无限级Dirichlet级数的增长性[J]. 华南师范大学学报:自然科学版,2003(4):27-31.
HUANG Zhibo,SUN Daochun.The growth of dirichlet series of infinite order[J].Journal of South China Normal University:Natural Science Edition,2003(4):27-31.
Keywords: Laplace-Stieltjes transforms; convergent abscissa; growth property
【责任编辑 庄晓琼】
THECONVERGENCEANDGROWTHOFLAPLACE-STIELTJESTRANSFORMS
LUO Xi1, SUN Daochun2
(1. School of Mathematics, Jiaying University, Meizhou, Guangdong 514015, China;2. School of Mathematics, South China Normal University, Guangzhou 510631, China)
By the new definition, some new results about the convergent properties of Laplace-Stieltjes transforms are obtained. Furthermore, a new function, which grows as quickly as the maximum norm function, is defined.
2009-02-23
国家自然科学基金资助项目(10471048)
罗茜(1981—),女,广东梅州人,嘉应学院助教,主要研究方向:函数论,Email:luoxi8100@yahoo.com.cn.
1000-5463(2010)01-0009-03
O175.55
A
