非负Ricci曲率紧致带边流行的刚性

吴筱怡,徐慧群

(杭州师范大学 理学院，浙江 杭州 310036)

0 引 言

在文献[1]中，作者研究了非负Ricci曲率紧致带边流形的刚性，得到如下结果：

定理A设Ω是(n+1)维具有非负Ricci曲率下界k≥0的紧致带边黎曼流形，非空边界M=∂Ω上有Ω的诱导度量，假设M的主曲率≥c>0，则λ1(M)≥nc2．

笔者改进了上述结果，得到如下结论：

1 预备知识

设Ω是带边界M=∂Ω的n+1维黎曼流形，f是定义在Ω上光滑到边界M上的函数．记

(1)

设{e1,…,en-1,en}是局部幺正标架，q∈∂Ω，e1,…,en-1切于∂Ω，en是外法向量．记

(2)

定义第二基本形式

(3)

平均曲率

(4)

文献[2]中有下列Reilly公式：

(5)

其中Ric(,)是Ω的Ricci张量．

2 定理的证明

定理的证明

设z是M上对应于特征值λ1的第一特征函数，即

Δz=-λ1z，

(6)

其中λ1=λ1(M)．

令f是下面Dirichlet问题的解：

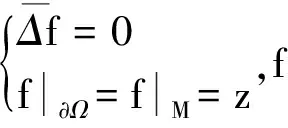
(7)

由式(5)得到

(8)

则有

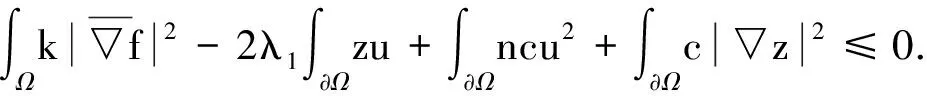
(9)

由式(6)，得到

(10)

所以有

(11)

再由于

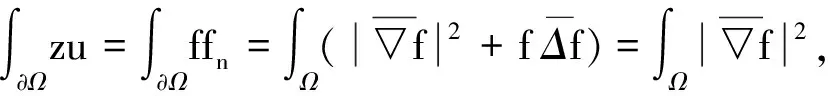
(12)

则有

(13)

从而

(14)

即

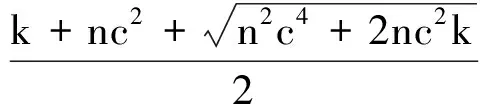
定理得证．

[1] Xia Changyu. Rigidity of compact manifolds with boundary and nonnegative and nonnegative Ricci curvature[J]. Proc AMS,1997,125(6)：1801-1806．

[2] Robert C R. Application of the Hessian operator in a Riemannian manifold[J]. Indianauniv Math J,1997(26):459-472．

[3] Zhong Jiaqing, Yang Hongcang. On the estimate of the first eigenvalue of a compact Riemannian manifold[J]. Sci Sin, SerA,1984(12)：1251-1265．

[4] Xia Changyu. Rigidity and sphere theorem for manifolds with positive Ricci curvature[J]. Manuscripta Math,1994(85)：79-87．