新巴塞尔协议信用风险度量模型的实证模拟——标准法、初级内部评级法和高级内部评级法的比较

沈庆劼

(天津财经大学 金融系，天津 300222)

一、文献回顾

信用风险是商业银行所面临的最主要风险，信用风险的度量模型分为传统与现代两大类型，传统模型包括Z计分模型、ZETA模型、Logit模型、MDA模型以及神经网络模型等；现代模型包括Credit Metric模型、KMV 模型、Credit Risk+模型、Credit Portfolio View模型、KPMG模型以及死亡率模型等。许涤龙[1]从模型的构建理论与适用性等角度分别对传统模型以及现代模型进行了比较。梁世栋[2]与曹道胜[3]专注于对其中现代模型的比较研究，梁世栋对主要派别的代表性模型用数学语言进行了总结，比较分析了各模型的原理及优缺点；曹道胜从模型建立的理论基础、模型类别、回收率、现金流折现因子四个维度进行了比较。实证方面，国外学者早在2000年，已开始运用模拟方法对模型进行了比较研究，Gordy[4]和Crouhy[5]在各自的研究中分别指出，各种不同的模型对在同一时点的相同资产组合进行评估时得出的结果是相近的。此外，Nickell[6]运用实际资产组合数据对模型进行了比较研究，但结果显示模型都未能很好的预测风险。与此相类似，张宗益、朱小宗等[7-8]采用重庆4家国有银行提供的1999—2004年1238家企业的贷款数据，分别对传统模型与现代模型进行了比较分析，与Nickell的结果相类似，研究结论也表明模型不能很好的预测风险。

巴塞尔协议所提出的信用风险度量模型包括标准法、初级内部评级法以及高级内部评级法。对于这三类已经在实际操作领域开始运用的模型，理论界的研究并不多见。刘伟[9]与韩瑾[10]对其进行了简单的比较。邓云胜[11]对内部模型法中违约概率(PD)与违约损失率(LGD)的估计模型进行了比较。目前，学术界对于新巴塞尔协议所提出的三种信用风险度量模型进行实证研究的论文尚不多见，本研究将基于模拟的方法对此进行研究。

二、模型分析

信用风险的测度模型包括标准法、初级内部评级法与高级内部评级法。标准要求，银行采用外部信用评级机构的评级结果来确定各项资产的信用风险资产数值。内部评级法允许银行使用自己测算的风险要素计算风险资产。其中，初级法仅允许银行测算与每个借款人相关的违约概率，其他数值由监管部门提供。高级法则允许银行测算其他必须的数值。

(一)标准法

标准法根据资产的不同类型，给予不同的风险权重。银行将资产规模与风险权重相乘，便可计算相应的风险资产数值。对于表内资产，《商业银行资本充足率管理办法》[注]中国银行业监督委员会2004年颁布，2006年修正，以下简称《管理办法》。第十七至第二十四条规定了不同资产的风险权重。对于表外资产，《管理办法》第二十七条规定，商业银行将表外项目的名义本金额乘以信用转换系数,获得等同于表内项目的风险资产，然后根据交易对象的属性确定风险权重，计算表外项目相应的风险加权资产。

(二)初级内部评级法

内部评级法允许银行使用自己测算的风险要素计算风险加权资产。对于主权、银行、公司类非违约风险暴露的风险加权资产，商业银行基于单笔信用风险暴露的违约概率(PD)、违约损失率(LGD)、违约风险暴露(EAD)以及有效期限(M)进行计算。对于住房抵押贷款、合格循环零售贷款和其它零售贷款的风险加权资产，商业银行基于单个资产池零售风险暴露的违约概率(PD)、违约损失率(LGD)以及违约风险暴露(EAD)和相关性(R)进行计算。对于主权、银行、公司类非违约风险暴露的风险加权资产，单笔信用风险暴露的风险加权资产为：

RWA=K×12.5×EAD

(1)

其中K为单笔信用风险暴露的资本要求，K的计算公式为：

(2)

其中N(·)表示标准正态分布概率，G(·)表示标准正态分布的逆函数，R表示贷款的资产相关系数，M表示贷款期限，b表示期限调整因子。表示贷款的资产相关系数R基于违约率PD计算，计算公式如下：

(3)

对于零售风险暴露的风险加权资产，商业银行应分别计算住房抵押贷款、合格循环零售贷款和其它零售贷款的风险加权资产。对于单个资产池信用风险暴露的风险加权资产，计算公式同(1)式RWA=K×12.5×EAD，其中K为单个资产池信用风险暴露的资本要求，K的计算公式为：

(4)

零售贷款单个贷款池的相关系数：个人住房抵押贷款相关系数为0.15，合格循环零售贷款相关系数为0.04，其他零售贷款相关系数计算公式如下：

(5)

对于零售风险暴露的风险参数，零售风险暴露的违约概率为商业银行内部估计的零售资产池的1年期违约概率和0.03%中的较大值。

(三)高级内部评级法

高级内部评级法允许商业银行对于风险参数——违约损失率、违约风险暴露与有效期限进行内部估计。《商业银行资本充足率计算指引》[注]中国银行业监督委员会2010年颁布并实施,以下简称《计算指引》。规定商业银行应通过内部评级确定每个非零售风险暴露债务人和债项的风险等级。商业银行可以对低风险业务或不能满足评级条件的风险暴露采取灵活的处理方法。商业银行可以采用计量模型方法、专家判断方法或综合使用两种方法进行评级。非零售风险暴露内部评级的技术要求包括评级维度、评级结构、评级方法论和评级时间跨度、评级标准、多种评级方法处理、模型使用和文档化管理等八个方面。

三、实验设计

由于三个模型的计算公式已经确定，所以只要给出任意一组自变量，三个模型都能够生成各自唯一的解。我们将通过随机模拟方法，生成若干组自变量，并根据随机生成的自变量，运用模型计算出相应的若干组解。模型运算所需的自变量包括银行资产组合比例与风险参数两类。

(一)资产组合的模拟

为了方便比较，将资产规模设为1。《管理办法》将表内资产类型分成了23种，将表外资产类型分成了7种，这30种资产类型我们都予以保留。《计算指引》在计算零售风险暴露的风险加权资产时，将该类资产分成了个人住房抵押贷款、合格循环零售贷款和其它零售贷款三类，其中的合格循环零售贷款是多出的内容，所以我们在上述30种的基础上，添加这一类型，最终将商业银行的所有资产分成31个类型。其中第i种资产的规模为ωi，可知

(6)

我们需要随机生成ωi，使其满足(6)式，且取值合理。为此，我们进行如下设计：生成30个在[0.1]上均匀分布的随机数rand(1)～rand(30)，使

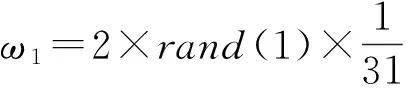
(7)

事先给定某一种或多种资产类型的比例，可以将给定的n个资产比例当作前n个资产比例，代入程序(7)，同样可以在Excel中随机生成所需的资产组合比例。

(二)风险参数的模拟

由于标准法外生给定了资产组合中各类资产的风险权重，所以只要给定资产组合中各类资产的比例，就能够计算出加权风险资产，无需设定风险参数。对于初级内部评级法与高级内部评级法，违约概率(PD)、违约损失率(LGD)、违约风险暴露(EAD)、有效期限(M)以及相关性(R)都是需要设定的风险参数，我们按照《计算指引》要求设定违约风险暴露、有效期限和相关性为定值，重点模拟违约概率和违约损失率不同取值对于模型加权风险资产数值的影响。表1给出了违约概率和违约损失率的基准值和变动区间，基准值为其固定不变时所取的值，变动区间为允许其变动时的变化范围。我们根据各变量现实中最可能的取值确定基准值与变动区间，其他外生变量都设定为常数。

表1 风险参数的基准值以及变动区间

四、模拟结果

数值模拟中，可以随机生成的自变量包括31个资产组合比例ωi以及2个风险参数违约率PD与违约损失率LGD，共33个变量。我们首先允许这33个自变量都随机生成，进行100次模拟，分别获得100个基于标准法的加权风险资产数值、100个基于初级内部评级法的加权风险资产数值以及100个基于高级内部评级法的加权风险资产数值。在下面的第一部分，我们就这300个数值进行比较，分析三种模型所计算的加权风险资产数值的总体大小情况。在下面的第二部分，我们研究这300个数值与某几个自变量之间的关系，分析这几个自变量对于三种模型所计算的加权风险资产数值的影响。然后，我们控制其他自变量，仅仅允许一个或两个自变量随机取值。在下面的第三部分，我们考察了在其他变量固定不变时，风险参数违——约率PD与违约损失率LGD的变化对三种模型结果的影响。

(一)三种模型结果的总体比较

我们允许31个资产组合比例ωi以及2个风险参数违约率PD与违约损失率LGD，共33个自变量按照我们在实验设计中给出的程序随机生成。进行100次模拟，基于《管理办法》以及《计算指引》，计算出了100个基于标准法的加权风险资产数值、100个基于初级内部评级法的加权风险资产数值以及100个基于高级内部评级法的加权风险资产数值。

图1以实验次数为横坐标，绘制出了3条分别连接这一百个点的折线。图2与3展示了标准法与初级内部评级法的差值以及初级内部评级法与高级内部评级法的差值。图4绘制了基于三个模型，模拟的加权风险资产数值的箱体图。

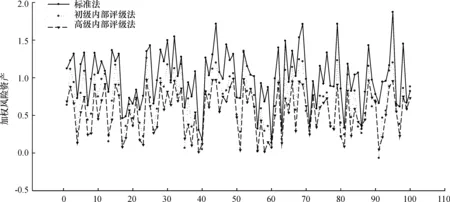
图1 信用风险加权风险资产模拟

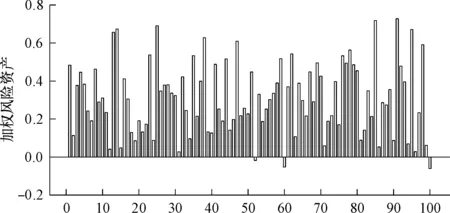
图2基于标准法与基于初级内部评级法计算的加权风险资产的差值

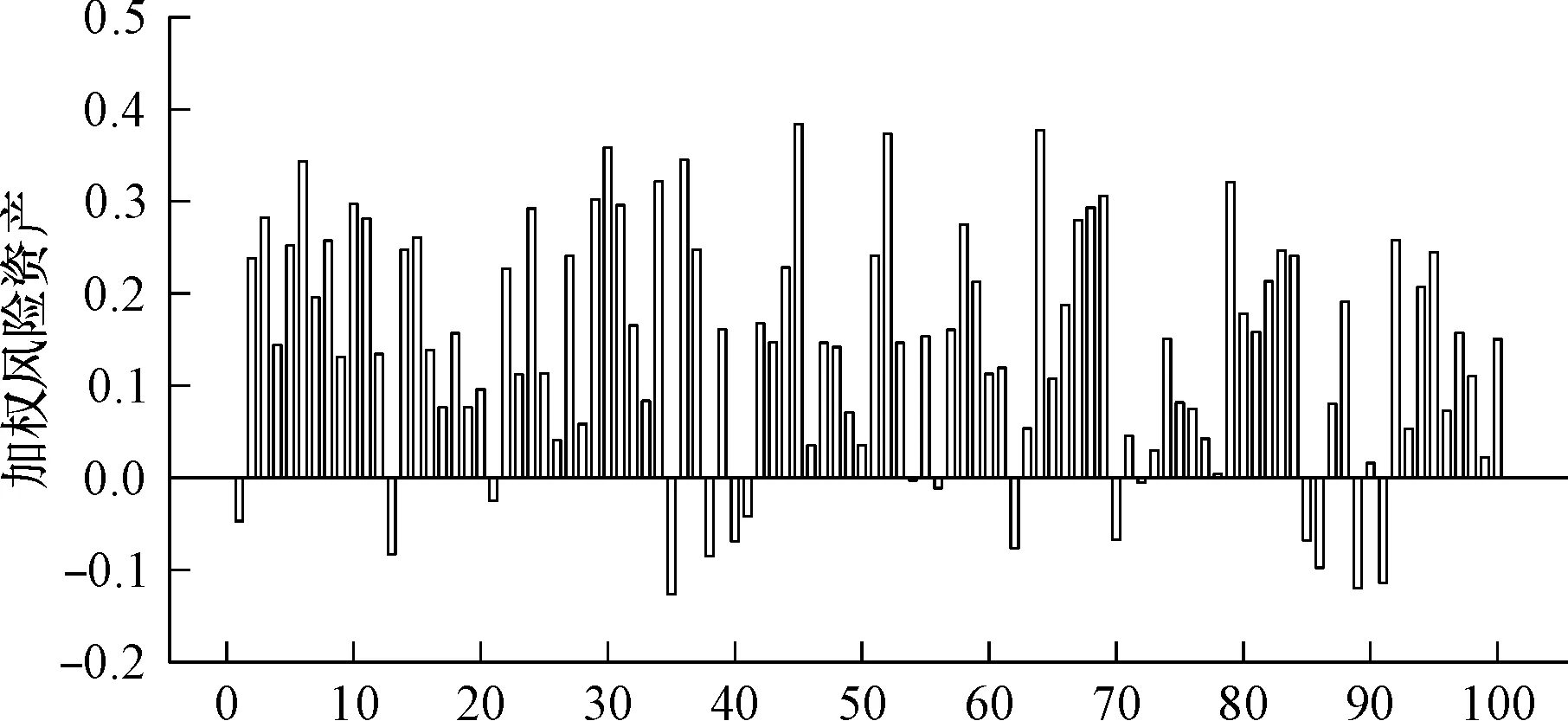
图3基于初级内部评级法与基于高级内部评级法计算的加权风险资产的差值

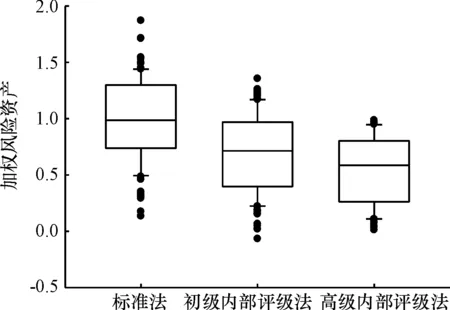
图4 信用风险加权风险资产模拟值的箱体图

由图1—图4我们可以得出以下结论：

第一，三种模型计算的加权风险资产数值上存在显著性差异。总体来说，标准法测度的加权风险资产数值最大，均值为1；初级内部评级法测度的加权风险资产数值其次，均值为0.7；高级内部评级法测度的加权风险资产数值最小，均值为0.6。

第二，三种模型的大小关系比较稳定。在100次模拟实验中，标准法测度的加权风险资产只有3次小于初级内部评级法测度的加权风险资产，且相差都在0.1以内。在100次模拟实验中，初级内部评级法测度的加权资产有将近20%的概率小于高级评级法测度的加权资产水平，相差均不大于0.2。

第三，三种模型数值跨度呈递减状态。标准法对于自变量比较敏感，而内部评级法尤其是高级内部评级法对自变量敏感性较弱。这可能是因为对于内部评级法，我们没有区分不同资产的风险参数，从而使得由资产组合比例差异所导致的风险加权资产的差异较小，图中显示出的相应变异主要来源于风险参数的变化。

(二)资产比例对三种模型结果的影响

为了研究资产组合中各类资产的比例对于模型结果的影响，我们分别关注某一资产类型的比例变化对于三种模型结果的影响。考虑各类资产的比例对于标准法与初级内部评级法差异，以及初级内部评级法与高级内部评级法差异的影响。

我们分别以31个资产组合比例ωi为横坐标，以标准法计算的加权风险资产与初级内部评级法计算的加权风险资产的差值，以及初级内部评级法计算的加权风险资产与高级内部评级法计算的加权风险资产的差值为纵轴，共生成62幅图。其中比较有规律性和代表性的结论见图5—图8，基于模拟结果，我们得出几点结论：

第一，个人住房抵押贷款占总资产的比例越高，使用越高级的风险度量技术计算的监管资本越少。即在个人住房抵押贷款占比较高时，使用初级内部评级法比标准法需要较少的监管资本，使用高级内部评级法法比初级内部评级法需要较少的监管资本。

第二，中央政府债权占比较多时，标准法计算的监管资本相对较低。因为标准法给予中央政府债权的风险权重为0，所以这部分资产在标准法下是无需监管资本要求的，而无论是对于初级内部评级法还是高级内部评级法，都不可能产生负的监管资本要求。

第三，企业和个人贷款占比越高，高级内部评级法相对于初级内部评级法的优势越弱。当企业个人贷款比较高时，选择高级内部评级法并不能够降低监管资本要求。

图5个人住房抵押贷款占比对标准法与初级内部评级法结果差值的影响

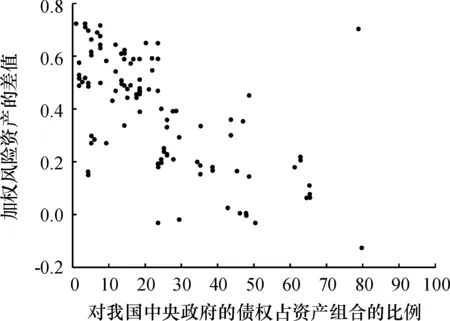
图6中央政府债权占比对标准法与初级内部评级法结果差值的影响

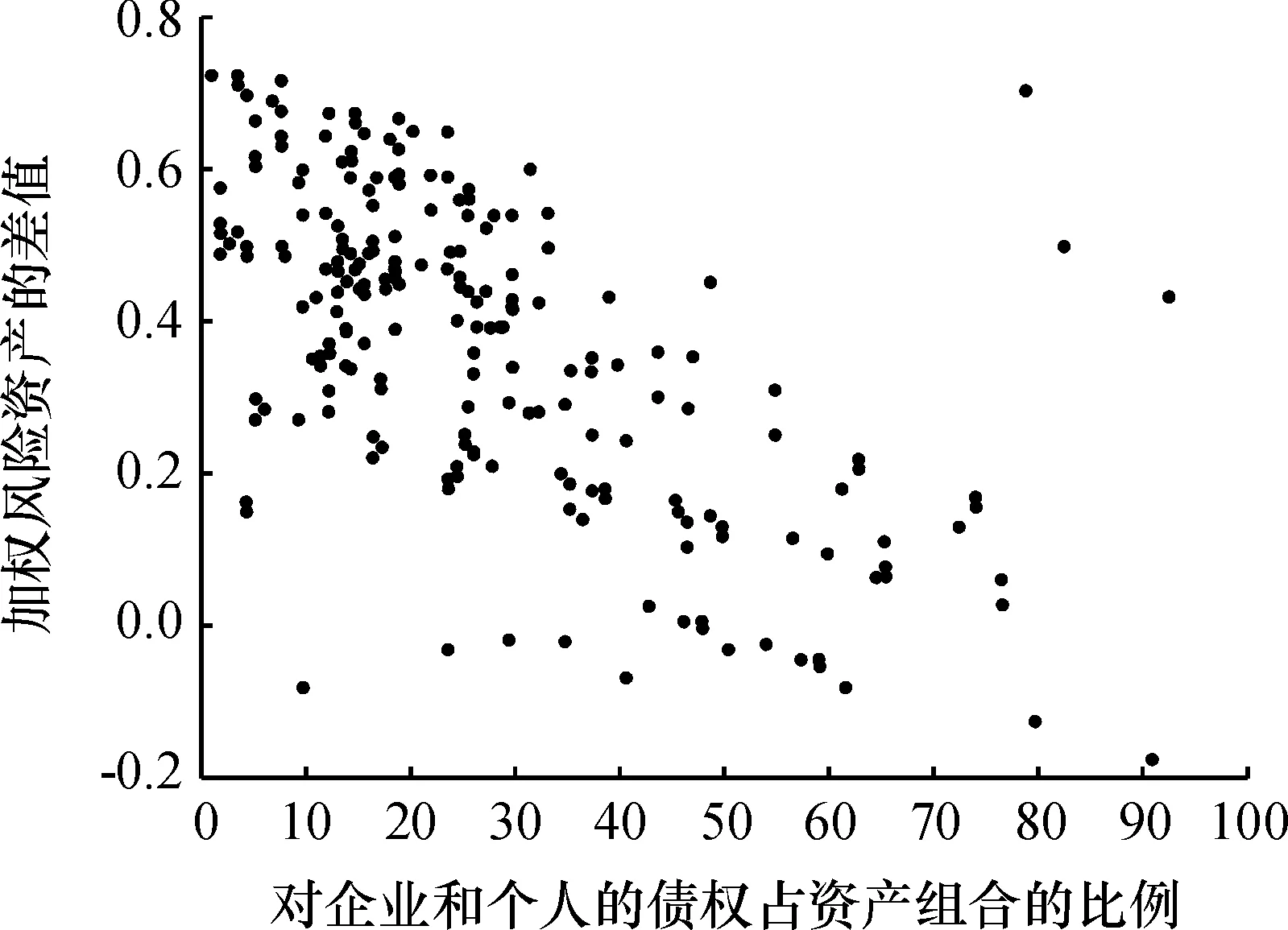
图7企业和个人债权占比对初级内部评级法与高级内部评级法结果差值的影响

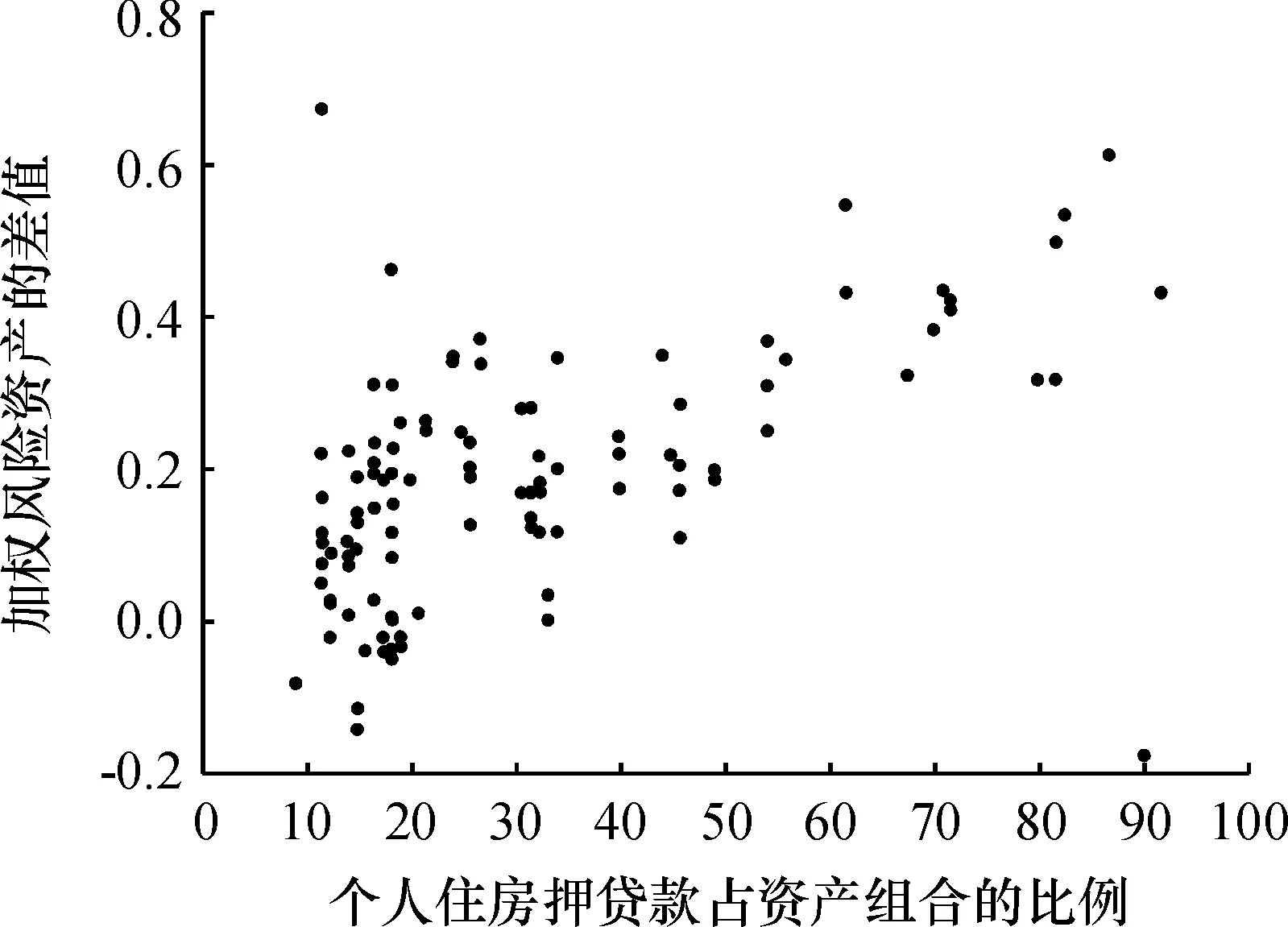
图8个人住房抵押贷款占比对初级内部评级法与高级内部评级法结果差值的影响

(三)风险参数对三种模型结果的影响

下面我们分析风险参数对于三种模型结果的影响。为了研究的简单起见，我们在考察一个参数的影响时，控制其他自变量固定不变。

我们首先控制贷款违约率以外的其他参数固定不变，让违约率在0—20%的区间上随机生成100个样本，根据之前固定的自变量数值以及模拟生成的违约率数值，分别模拟出100个基于标准法的风险加权资产、100个基于初级内部评级法的风险加权资产以及100个基于高级内部评级法的风险加权资产，见图9。同理，我们控制其他自变量为固定常数，随机生成100个违约损失率的数值，见图10。

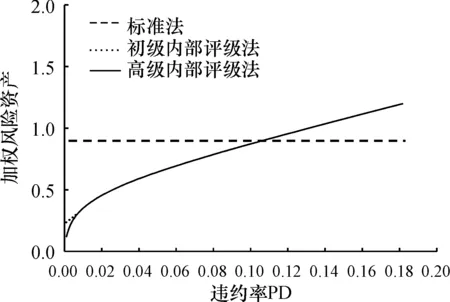
图9贷款违约率对于标准法、初级内部评级法以及高级内部评级法结果的影响

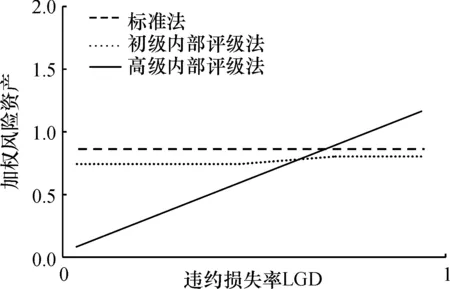
图10贷款违约损失率对于标准法、初级内部评级法以及高级内部评级法结果的影响

从图9、图10可以得出以下结论：风险参数表示资产的风险状况，风险状况不同，三种模型计算出的监管资本将存在巨大差异。资产风险越低，越高级的测度模型所需的监管资本越少。标准法的监管资本与资产的风险状况无关，违约率对于初级内部评级法与高级内部评级法的影响几乎等同，在大部分情况下两者重合。违约损失率对于高级内部评级法与初级内部评级法的差异存在重要影响。

为了研究违约率与违约损失率对模型差异的共同影响，我们在图11中允许两者同时变动，在一个三维空间中进行分析。由于初级内部评级法与高级内部评级法的计算思路一样，只是在违约率与违约损失率的取值上有差别，所以我们在此不予分析。我们着重考察违约率与违约损失率的变化对于高级内部评级法与标准法结果的差异性。

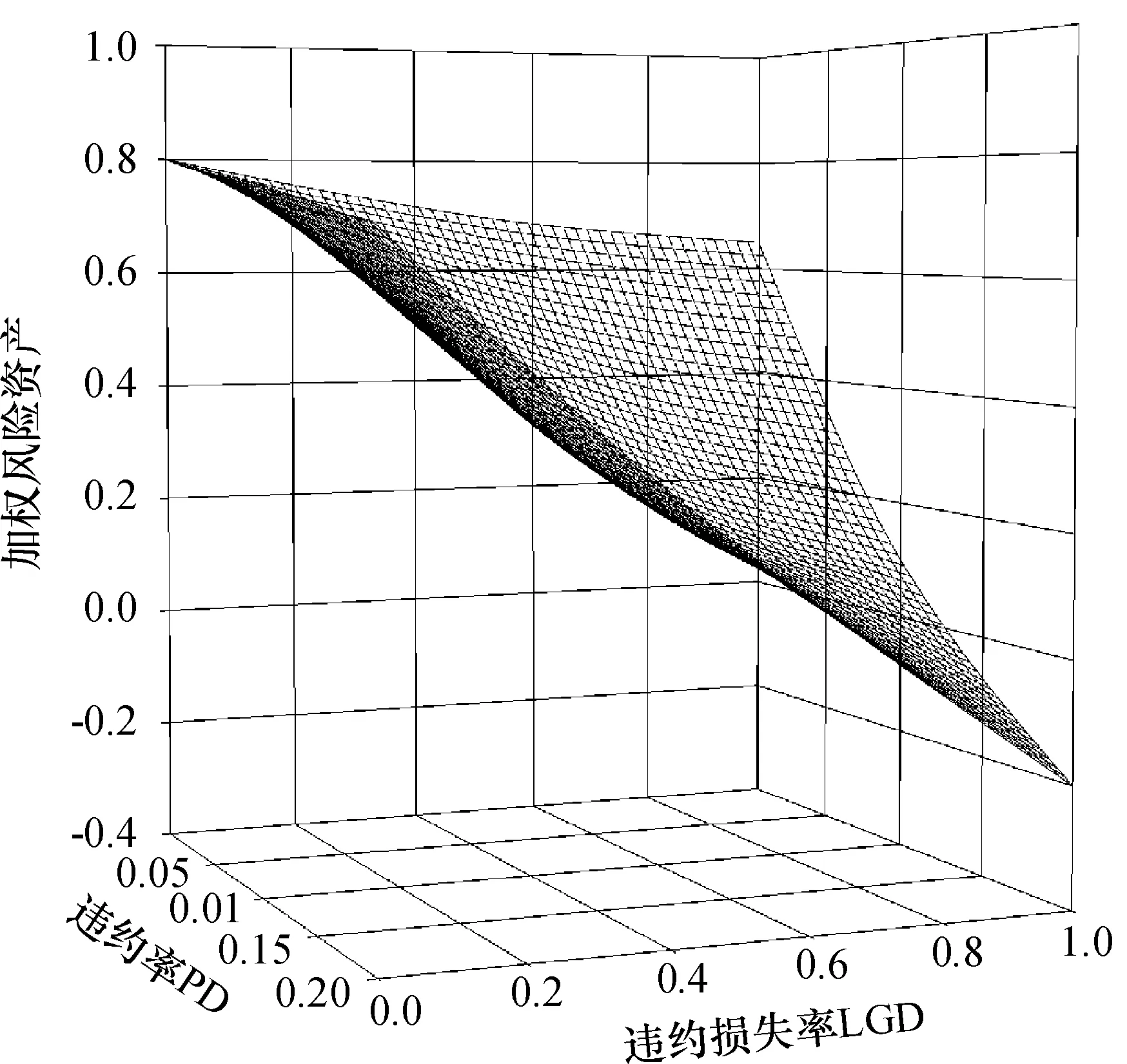
图11 贷款违约率与违约损失率对于标准法与高级内部评级法差异性的影响

根据图11得出：违约率与违约损失率对于高级内部评级法与标准法测算结果的差异性存在巨大影响。贷款违约率越高，差异性越大：违约损失率越高，差异性越大。在给定的参数区间内，大部分情况下差值为正数，只有在违约率以及违约损失率都很低的情况下，才会出现高级内部评级法测算结果小于标准法测算结果的情形。并且违约率以及违约损失率两个变量对数值结果差异性的影响是独立的，不存在联动关系。

五、结论与建议

本文研究表明：三种度量模型计算的加权风险资产，在数值上存在显著性差异，越高级别的模型所测度的加权风险资产数值越低；在商业银行的资产组合中，个人住房抵押贷款、中央政府债权、企业和个人贷款占总资产的比例对模型结果的差异性存在显著性的影响；资产组合风险水平越低，越高级的测度模型所计算的加权风险资产数值越低。

上述结论的政策含义在于：

第一，巴塞尔风险度量模型更多的是站在监管者角度控制风险，其对于风险的度量并不精确。巴塞尔风险度量模型力图做到简单、客观、难以被操纵，其在风险度量准确性上必然存在一定缺陷。商业银行可参考巴塞尔协议提供的度量模型设计自己的内部模型，但应尽力做到内部模型与监管模型相分离，为两种不同的目的设置两套不同的风险度量系统。

第二，当前中国处于新旧巴塞尔协议交叉重叠阶段，制度上允许商业银行选择不同的风险度量模型，而度量模型间存在显著性差异，且差异性本身存在内在规律性，这为商业银行提供了监管资本套利的可能性。商业银行可根据其资产组合与风险参数的特征，选择风险值较低的模型，以节约监管资本，从而提供单位资本的利润水平。

第三，监管部门应充分把握度量模型之间的差异性以及模型各自的特点，关注模型的适应性检测，并在贯彻巴塞尔协议第一支柱的条件下，认真执行第二支柱与第三支柱。

参考文献：

[1] 许涤龙,李 峰.金融机构信用风险度量模型的发展与比较[J].统计与决策,2009,(8).

[2] 梁世栋,等.信用风险模型比较分析[J].中国管理科学,2002,(2).

[3] 曹道胜,何明升.商业银行信用风险模型的比较及其借鉴[J].金融研究,2006,(10).

[4] GORDY. A comparative anatomy of credit risk models[J].Journal of Banking and Finance, 2000, 24 (1/2):119-1491.

[5] CROUHY,GALAI,MARK.A comparative analysis of current credit risk models[J].Journal of Banking and Finance,2000,24(1/2):59-1201.

[6] NICKELL,PERRAUDIN,VAROTTO.Ratings versus equity-based credit risk models:an empirical investigation[R].(2001-06-01).http:∥www.bankofegland.co.uk/publications/working papers/wp132.pdf.

[7] 张宗益,等.传统信用风险度量模型的实证比较与适用性分析[J].预测,2005,(2).

[8] 朱小宗,等.现代信用风险度量模型的实证比较与适用性分析[J].管理工程学报,2006,(1).

[9] 刘 伟.我国信用风险计量方法的合理选择[J].商业时代,2004,(26).

[10] 韩 瑾,等.新巴塞尔协议下资本计量方法比较研究[J].商业时代,2008,(11).

[11] 邓云胜,等.商业银行内部信用评级方法的比较研究[J].当代财经,2004,(9).