电网节点编号优化算法的改进
2010-11-16刘启蒙戈文江
刘启蒙,杨 鉴,戈文江
(1.华北电力大学,河北 保定 071003;2.河北建投新能源有限公司,石家庄 050001;3.河北省电力研究院,石家庄 050021)
0 引言
由于导纳矩阵节点消去过程中会注入新的非零元素,而消去过程注入新的非零元素与导纳矩阵中的元素排列有关,也就是和节点编号顺序密切相关,不同节点编号方案所产生的注入元素数目也不相同,因此为了充分利用电力网络模型矩阵的稀疏特性,减少不必要的计算,提高求解效率,有必要对网络节点进行节点编号优化。节点编号优化严格地说是一个组合优化问题,针对不同电网结构会采取不同的节点编号优化方法,对于辐射配电网可采用树状编号、逆流编号等算法,对于复杂电力网络会有大量的节点编号方案,很难求出最优方案,因此目前实际工程应用中广泛采用的是求次优编号的方法,如静态优化法、半动态优化法和动态优化法3类传统优化算法。
1 传统优化算法简介
1.1 静态优化法
根据导纳矩阵消去过程可知,导纳矩阵小行号的非零元素越少,消去过程中注入新的非零元素越少。导纳矩阵的行号就是网络的节点号,其每行的非零元素就是相应节点所连接的支路数(非对地支路),因此按照连接支路最少的节点顺序编号,就是静态优化法。编号前,统计网络各节点连接支路数,支路少的优先编号,若支路相同,则顺序编号。静态优化法的主要特点是优化快,编程简单,但优化效果差。
1.2 半动态优化法
该方法的基本思想是找到连接支路最少的节点进行编号,然后消去该节点,每消去一个节点,尚未编号节点的支路连接数就会发生变化,然后从未编号节点中查找连接支路最少的节点进行编号。如此反复,直到消去所有节点。半动态优化法考虑了各节点出线数目的变动情况,注入元素减少,具有优化效果好,编程简单,优化快等优点,但与动态优化法相比元素仍然过多。
1.3 动态优化法
动态优化法分为两步,第一步是将网络的所有节点轮流进行一次消去运算,统计各节点消去后各自增加的新支路数,将增加支路数最少的节点编号为1,然后消去该节点;第二步是将尚未编号的每个节点依次进行一次消去运算,统计各节点消去后各自增加的支路数,将增加支路数最少的节点编号为2,随后消去该节点。依此类推,对尚未编号的节点全部按照此操作,即完成节点编号优化。从理论上说,动态法的优化效果最好,但优化速度慢,运算量大。
2 优化算法的改进
以下根据电力网络节点编号优化问题的特点,设计了一套结合动态法和半动态法优点的改进优化方法,来完成节点编号优化。
a. 对电网循环查找出线度(节点连接支路数)为1的节点,对该节点进行优化编号(因为消去该节点不会产生新的注入元素),消去该节点。该节点对端节点的出线度会因为消去该节点而改变,因此消去该节点后,应重新计算对端节点的出线度。
b. 对电网循环查找出线度为2的节点,按消去该节点所产生的注入元素最少进行优先编号,产生注入元素相同的节点进行随机编号。消去该节点后,重新计算对端节点的出线度。
c. 对电网循环查找出线度为3的节点,按消去该节点所产生的注入元素最少进行优先编号,产生注入元素相同的节点进行随机编号。消去该节点后,重新计算对端节点的出线度。
d. 当所有节点的出线度都大于等于4后,只按照出线度的多少进行编号,不再重新计算消去节点后对端节点的出线度(导纳矩阵是稀疏矩阵,在节点出线度大于4时,计算消去该节点产生注入元素的时间过长,计算过程繁琐)。该方法结合了半动态法和动态法编号的优点,充分利用了电力网络的稀疏特性。该方法与半动态法相比,每次编号都是在最少出线度的相同节点中选择消去该节点后注入元素最少节点进行编号,而不是在出线度相同的情况下随机编号,所以新的非零注入元素小于半动态法,提高了矩阵的稀疏度,矩阵处理起来比半动态法容易;与动态法相比,优化效果相当,但是由于每次编号是在出线度最少的节点中考虑优先编号,而不是对整个电网所有节点进行消去,每次循环涉及的节点数量减少,循环次数大大降低,速度明显提高。
3 算例分析与比较
3.1 算例分析
图1为某电网系统等值电路(15个节点,20条支路),以下分别采用动态优化法和以上提出的改进优化法对其进行节点编号优化,并分析优化结果。
选用动态法对该网络的优化编号顺序为:1、2、15、5、8、4、3、6、7、13、14、9、10、11、12。

图1 电网系统等值电路
选用以上提出的改进优化法对该网络进行优化编号的具体步骤为:
a. 查找出线度为1的节点,查找结果为1节点,消去1节点,计算对端节点2的出线度,得2的出线度为1,消去节点2,计算对端节点3的出线度为3。
b. 查找出线度为1的节点,查找结果为节点15,消去节点15,计算对端节点12的出线度,得12的出线度为3。此时网络中无出线度为1的节点,得到优化后的拓扑结构见图2。
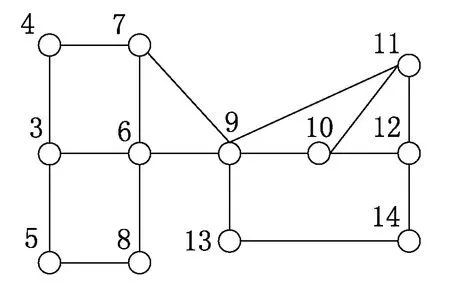
图2 节点1、2、15优化后的拓扑结构
c. 查找尚未编号节点中出线度为2的节点,查找结果为节点4、5、8、13、14。由于消去节点4、5、8、13、14,都产生一个注入元素,故可随机编号,可选取5节点进行编号,消去节点5,计算对端节点3、8的出线度。
d. 由于上一步消去后,节点3、8的出线度都不变,因此出线度为2的节点为4、8、13、14。由于消去节点8没有注入元素,而消去节点4、13、14,均产生一个注入元素,所以消去节点8。然后计算可知,节点8对端节点3的出线度为2,节点6的出线度为3。此时优化拓扑结构见图3。
e. 节点3、4、13、14的出线度为2,并且消去这4个节点的注入元素均为1,故可随机编号,可选取4节点进行编号,消去节点4,计算对端节点3、7的出线度。
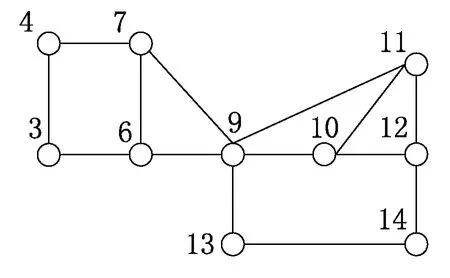
图3 节点5、8优化后的拓扑结构
f. 节点7的出线度为3,节点3、13、14的出线度为2,由于消去节点13、14均产生一个注入元素,消去节点3无注入元素,故消去节点3。计算对端节点6、7的出线度。
g. 计算可知,节点6、7、13、14的出线度均为2,消去节点6、7无注入元素,消去节点13、14注入元素为1。故随机消去节点6,计算对端节点7、9的出线度。
h. 计算可知,节点7的出线度为1,节点9的出线度为4,故消去节点7,计算得对端节点9的出线度3。此时优化拓扑结构见图4。
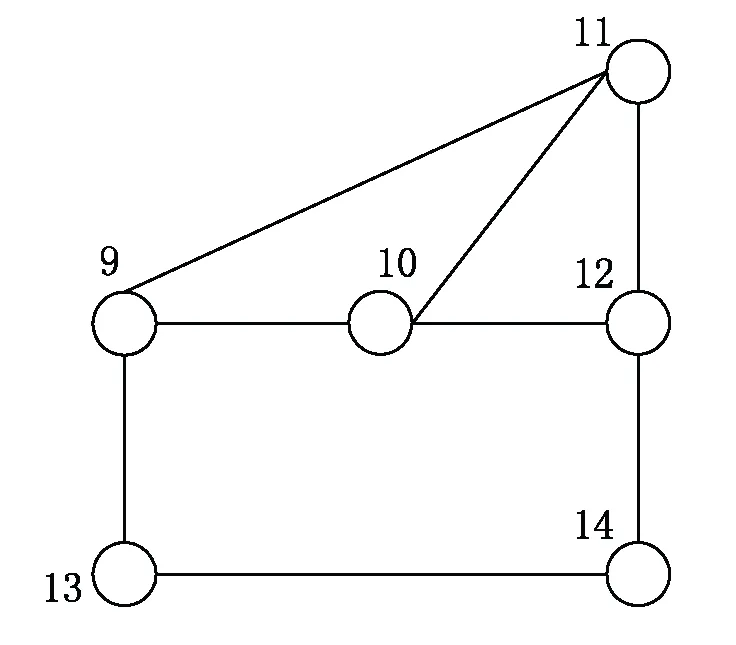
图4 节点4、3、6、7优化后的拓扑结构
i. 查找出线度为2的节点,查找结果为节点13、14,由于消去节点13、14均产生一个注入元素,故随机消去节点13。
j. 计算对端节点9、14的出线度可知,节点9的出线度为3,节点14的出线度为2,故消去节点14。
k. 计算节点14对端节点9、12的出线度,可知节点9、12的出线度均为2。
l. 计算可知,消去节点9、12后分别产生的注入元素均为0,故随机消去节点9。此时优化拓扑结构见图5。

图5 节点13、14、9优化后的拓扑结构
m. 计算对端节点10、11、12的出线度,可知节点10、11、12出线度均为2,消去这3个节点都无新的注入元素,故随机消去节点10。
n. 计算对端节点11、12的出线度,可知节点11、12出线度均为1,故随机消去节点11。
o. 消去节点12。
至此网络节点编号全部形成,优化编号顺序结果为:1、2、15、5、8、4、3、6、7、13。
3.2 计算量比较
通过以上的算例分析可知,以节点优化过程中需要进行消去运算的总的元素个数作为计算量,按照传统的动态优化法,需要对75个元素进行消去运算,而以上提出的改进优化算法只需要对31个元素进行运算即可,减少的计算量为58.66%,而优化结果和动态优化法结果相同,可见该算法的优化效果明显。
为论证该算法对高电压等级和大电网的适用性,以宁夏电网的18节点、61支路的子网为例,用C++语言进行编程计算,其结果表明与传统的动态节点编号优化法相比,采用以上提出的改进优化算法,计算时间可减少50%,而且随着电网节点和支路数以及拓扑复杂度的增加,其优化效果更加明显。
4 结束语
传统的电力网络节点编号优化方法中,由于静态优化法优化快,编程简单,但优化效果差,半动态法和动态法优化效果明显,但过程较复杂,在实际应用中受到一定限制。以上根据电力网络节点编号优化问题的特点,设计了一套结合半动态法和动态法优点的改进优化算法,并进行了实例验证,结果显示,该方法在优化效果和时间上较传统方法有了很大的提高,可以达到理想的优化效果,对大规模复杂电网的计算机辅助分析计算具有重要的参考价值。
参考文献:
[1] 罗 军,于歆杰.基于遗传算法的稀疏节点优化编号方法[J].电网技术,2006,30(22):54-58.
[2] 乐全明,吕飞鹏,王菊萍,等.形成节点阻抗矩阵的节点编号顺序优化算法[J].电网技术,2006,30(6):88-91.
[3] 彭春华,徐雪松.基于蚁群算法的电力网络节点编号多方案优化[J].电力系统及其自动化学报,2007,19(2):60-65.
[4] 徐得超,李亚楼,郭 剑,等.消去树理论及其在潮流计算中的应用[J].电网技术,2007,31(22):12-16.
