非概率可靠指标发展及其求解方法概述

张盈盈,邓 建,霍婷婷

(中南大学资源与安全工程学院, 湖南长沙 410083)

非概率可靠指标发展及其求解方法概述

张盈盈,邓 建,霍婷婷

(中南大学资源与安全工程学院, 湖南长沙 410083)

系统地介绍了非概率可靠性度量指标的发展状况,对应用最为广泛的凸集比例因子非概率可靠指标,概述了其求解方法,分析了隐式极限状态方程问题的研究现状,并就其发展趋势提出了意见。

非概率可靠指标;凸集比例因子;求解方法;隐式极限状态函数

传统的可靠性分析围绕不确定性而展开,一般采用以概率为基础的随机模型和模糊模型来处理不确定性。但为了定义参数的概率分布或隶属函数,概率模型通常需要较多的数据。有研究表明,在对技术要求严格的情况下,概率模型的细微差错或数据缺乏可能导致可靠性分析的较大误差。1990年以来,Ben-Haim和 Elishakoff等最早提出非概率可靠性的概念,认为当掌握的数据信息较少时,宜采用集合模型来描述不确定性的变化范围。由于所提的非概率可靠性概念完全不涉及概率,可以克服传统概率模型无法解决的困难,很多学者对其进行了研究。本文主要介绍非概率可靠指标的发展,重点介绍当前应用最为广泛的凸集比例因子指标及其求解方法,并探讨其发展趋势。

1 非概率可靠指标发展概述

目前,非概率可靠性分析处于初步研究状态,可靠性领域尚未形成统一的非概率可靠指标,现有可检索文献中共有 4种:凸集最小扩展函数指标[1]、安全因子指标[2]、最小无穷范数指标[3]、凸集比例因子指标[4]。

1.1 凸集最小扩展函数非概率可靠指标[1]

Ben-Hai m认为如果结构在失效前能够承受较大的不确定性,则是可靠的。并基于凸集不确定性模型及其 ET特性 (扩展和平移特性),提出把系统承受不确定性的最大程度作为衡量非概率可靠度的指标。

非概率可靠指标定义为:

该指标用于求解线性系统且输入集合为单一集合的问题。它表征了结构允许的不确定性变化的最大尺度,与当前的不确定性无关。因此无法判定在某种给定条件下系统的安全程度,也无法比较不同系统之间的安全程度。而且文献[1]仅针对简单问题提出求解可靠指标的解析公式,没有相应的数值算法,无法用于求解复杂问题。虽然该指标适用的凸集不确定性模型的种类较多,但由于上述种种缺陷,未得到广泛的应用[4]。

1.2 安全因子非概率可靠指标[2]

安全因子非概率可靠指标由 Elishakoff于 1995年在针对Ben-Haim提出的非概率可靠性的概念的讨论中提出的一种度量方法。

非概率可靠指标 r定义为:

r为一区间变量。当系统安全时,安全因子 Sf>1,此时 r∈(0,1),r所在区间越靠近 1,该系统越安全;当系统失效时,r∈(-∞,0),所在区间越靠近 -∞,系统越不安全[4]。

该指标实际上是传统的安全因子法和区间算法的简单结合。由于指标值为区间变量,不同系统间无法做精确的比较,限制了其应用。

1.3 最小无穷范数非概率可靠指标[3]

该指标是郭书祥在区间算法基础上,提出的度量非概率可靠度的新方法。基本思想是:把结构性能在指定条件下的变化范围与要求的变化范围作比较,以衡量结构的安全程度。

(1)基本定义。设基本变量 xi为区间变量,即则 xi的均值为离差对 xi做标准化变换:xi=+其中,△ =[-1,1]为标准化区间,δ∈△为标i准化区间变量。取M=g(x)=g(x1,x2,…,xn)为由结构失效准则确定的功能函数,M=0即为失效面,M<0和M>0分别表示结构处于失效状态和安全状态。当 g(·)为 xi的连续函数时,求得M的均值Mc和离差Mr,定义非概率可靠指标η为:

(2)扩展定义。从几何角度分析,得到该指标的扩展定义:在标准化区间变量的扩展空间中,按无穷范数‖·‖∞度量的从坐标原点到失效面的最短距离。即:

满足条件:M=g(x1,…,xn)=G(δ1,…,δn)=0。其中,δ={δ1,…,δn}为标准化区间变量,‖δ‖∞=max(|δ1|,|δ2|,…,|δn|),扩展空间指标准化区间变量扩展后的无限空间。若η=1,结构处于可靠和不可靠的临界状态;若η>1,基本区间变量的取值区域与失效域不相交,结构可靠。且η值越大,实际取值区域离失效域越远,结构的鲁棒性越高。

该指标既考虑了当前不确定性的大小,又是一个无量纲的数值,不但可以度量当前不确定因素下系统的安全程度,而且可以对不同系统的安全程度进行比较。它以极限状态方程为分析基础,易于理解,易于求解,线性、非线性问题均可处理,曾被广泛应用。但是该指标将结构的不确定参数单纯描述为区间变量,限制了其对其他不确定凸集模型的应用。

针对上述问题,易平提出区间不确定性可由区间变量或凸集合模型来描述,并通过具体算例对基于区间模型和基于凸集合模型的区间不确定性进行了比较研究,认为基于凸集合模型得到的可靠指标更接近于实际,而基于区间模型所得到的可靠指标过于保守,其实质就是“最坏的情形也不失效的结构才可靠”,追求的是结构的绝对安全[5]。因此,基于凸集合模型的非概率可靠指标是一种更经济、合理的指标。

同时,张新峰认为两种指标之间存在着确定的函数关系,并以二维的应力——强度模型为基础,通过理论计算进行了证明。同时得出,区间模型所包含的不确定域包含椭圆凸集合模型的不确定域,而工程中实际发生在椭圆凸集合模型的不确定域之外的概率非常小[6]。因此,基于凸集合模型非概率可靠指标比较符合工程实际。

1.4 凸集比例因子非概率可靠指标[4]

该指标是由刘成立在凸集最小扩展函数指标和最小无穷范数指标的基础上所提出,它适用于各类极限状态函数、各种凸集不确定性模型,弥补了以上几种非概率指标的缺陷。

若不确定性变量集合为:

引入不确定凸模型的比例放缩因子λ,构建集合族:

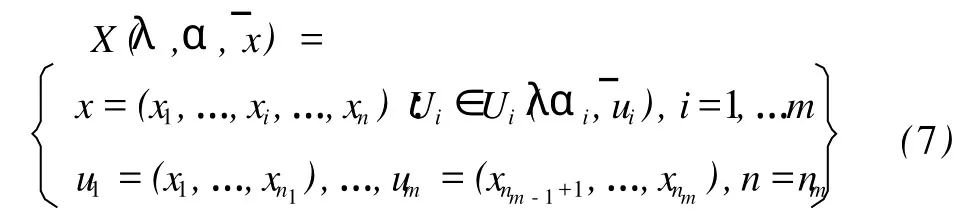
该不确定性集合族通过比例因子λ自由缩放。当凸集合族与失效域不相交时,结构安全;当凸集合族增大与失效域相交时,结构失效。因此,比例因子的大小反应了结构对不确定性因素的可靠性,定义总不确定性凸集合族增大到失效域的最小λ值为结构的可靠指标η:

若不确定性因素所在的凸集模型可以表示为:

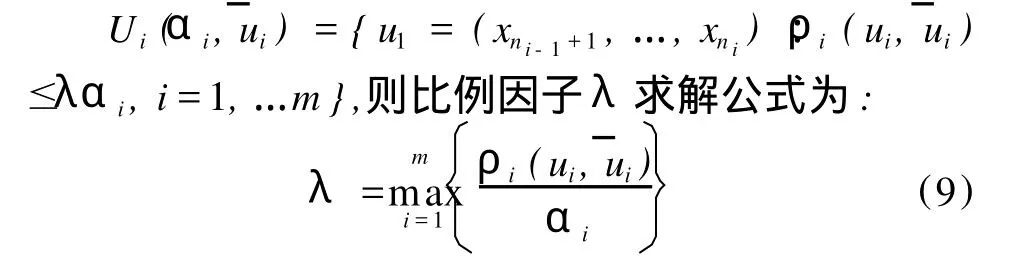
1.5 其它度量方法的比较分析

针对最小无穷范数非概率可靠性度量指标单纯将不确定性描述为区间模型的缺陷,很多学者对其进行了改进研究,并提出了度量方法。

冯世琪提出了一种新的度量方法,即:将描述结构不确定参数的区间变量内接于椭球之中,得到体积最小的椭球的壳体方程,可靠指标η定义为:按无穷范数度量的从椭球的壳体到失效面的最短空间距离[7]。笔者认为,虽然该度量方法在求解中用椭球凸集模型来模拟结构的不确定性,但仍建立在将不确定参数描述为区间变量的基础上,并未从根本上克服最小无穷范数指标的缺陷。

曹鸿钧提出一种可用于超椭球凸集模型与区间变量共存情况下的新的度量方法,其基本思想是:将各超椭球凸集转换为一个等效的单位超球,在新的变量空间中,根据各单位超球集合与结构功能函数的失效域之间的位置关系定义结构的可靠指标[8]。但作者在进行可靠指标与结构失效频数的比较时,求解失效频数的Monte Carlo仿真中人为假设了结构不确定参数的分布形式,因此,虽然比较结果说明该可靠指标是安全有效的,但不够严谨。而且从超椭球凸集转换为等效的单位超球的过程较为复杂。

2 凸集比例因子非概率可靠指标求解方法

目前针对该指标的求解,有 3类方法:解析方法、数值模拟方法、优化方法[4]。其中的数值模拟方法,需要将某些变量假定为随机变量,给出分布形式以及在凸模型内的抽样公式。笔者认为,非概率可靠性正是针对概率可靠性方法需要较多数据信息,而实际工程中难以得到足够的数据信息来准确定义概率模型及其具体的分布形式这一局限性而提出的,故不推荐使用数值模拟方法。因此,主要介绍解析方法和优化方法。

2.1 解析方法

2.1.1 解析法[4]

解析法用于求解线性极限状态函数问题。由凸集比例因子指标的定义可知,求解满足式 min(g(x))=0的η即可。其中,x∈X(η α)。由线性系统在凸集上的极值的性质得:(ρi(ui))2-η2α2i=0,构造如下拉格朗日函数,求解可得η。

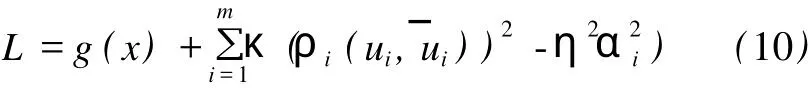
其中,κ为拉格朗日乘子,ui=(xui-1+1,…,xni),下标n0=0,nm=n。

2.1.2 一阶设计点法[4]

一阶设计点法是求解非线性极限状态函数问题的近似解析方法。其思路来自传统可靠性分析中改进的一次二阶矩法,即在设计点上将原始非线性极限状态函数展开成泰勒级数形式,仅保留常数项与一阶项,从而将非线性极限状态函数问题近似为线性极限状态函数问题。而后可采用上述的针对线性极限状态函数求解的一般解析方法求解。

该方法计算量较小,为实际工程中求解非线性极限状态函数的非概率可靠性提供了一种可行的近似分析方法。但由于仅用到泰勒展开式的常数项与一阶项,使得该方法在求解非线性程度不大的问题时精度较高,而针对非线性程度高问题的求解,特别是一阶导数不连续问题,计算结果可能不正确。

2.2 优化方法

该非概率可靠指标的求解可以转化为如下有约束的非线性优化问题的求解:

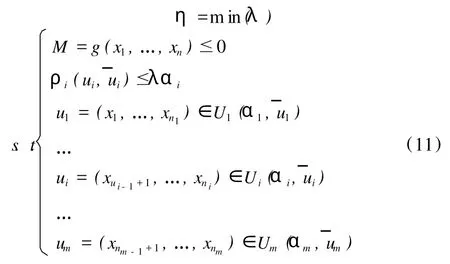
(1)基于 MATLAB优化工具箱的求解方法。可以直接使用Matlab优化工具箱的求解器进行求解。该方法计算速度较快,精度和稳定性也较高。但对非线性程度较高的问题很容易陷入局部最优解。

(2)其它全局优化算法。模拟退火算法和遗传算法作为全局优化方法,已经被成功运用到非概率可靠指标的求解问题中,且精度较高[4]。其中,模拟退火算法通用性、鲁棒性强,可用于求解复杂非线性优化问题,但应用时要注意其性能与初始值有关,参数敏感等问题。遗传算法是一种无需导数信息的概率搜索算法,处理非线性程度较高的极限状态函数问题有明显优势。

变尺度混沌优化方法在继承了基本混沌优化方法的思路直观、无需求导、容易程序化实现的优点的基础上,通过不断缩小基本变量搜索区间并提高搜索精度,克服了混沌搜索具有一定的盲目性、局部搜索能力不好等缺陷,具有较高的搜索效率[9]。文献[9]中,作者运用该方法较好地求解了非线性极限状态函数问题。

蚁群优化算法综合运用了正反馈、分布式计算和贪婪式启发搜索技术,可用于求解一般形式的非凸、非线性约束优化问题,不涉及目标函数的偏导数计算,且能够克服其他算法容易陷入局部最优的缺点,具有较强的适应性[10]。目前,蚁群算法已经成功应用于求解传统概率可靠指标问题中。笔者认为该算法同样能应用非概率可靠度的问题求解中。

2.3 隐式极限状态函数问题的求解现状

非概率可靠指标的求解以极限状态方程为基础,所以上述求解方法都是基于显式极限状态函数进行研究。对于隐式极限状态函数的问题,如何更为近似地拟合极限状态函数,是可靠指标求解精度的关键所在。仅文献[11]提出一种基于支持向量机回归求解非概率可靠指标的方法,文献 [4]提出先采用线性加权响应面法、二次响应面法或人工神经网络方法来显化隐式极限状态函数,再应用显式极限状态函数的分析方法求解可靠指标。其他关于求解基于凸集模型的隐式极限状态函数的非概率可靠度的研究笔者尚未查到。例如,如何通过响应面函数的选取、试验设计、模型参数的确定等方法来提高响应面法拟合极限状态函数的精度也是需要进一步研究的重要课题。

3 发展趋势

结构的非概率可靠性模型大大降低了对原始数据的要求,只需已知不确定参量的界限,而不要求其具体的分布形式,且计算简便,在实际工程中具有较好的适用性,是传统可靠性模型的有益补充。在所有的非概率可靠指标中,凸集比例因子非概率可靠指标最合理,应用最为广泛。就其目前的研究现状来看,首先,对于隐式极限状态方程的非概率可靠指标的求解有待于进一步研究。比如,如何通过响应面函数的选取、试验设计、模型参数的确定等方法来提高响应面法拟合极限状态函数的精度等等。其次,引入各种成熟的优化算法,可以为非概率可靠指标的求解带来极大方便。除了本文中提到的几种全局优化算法,还可以尝试引入其它优化算法来高效、精确地求解非概率可靠性问题。

[1] Ben-Haim Y.A non-probabilistic measure of reliability of linear systems based on expansion of convex models[J].Structural Safety,1995,17(2):91～109.

[2] Elishakoff I.Discussionon:A non-probabilistic concept of reliability[J].Structural Safety,1995,17(3):195～199.

[3] 郭书祥,吕震宙,冯元生.基于区间分析的结构非概率可靠性模型[J].计算机力学学报,2001,18(1).

[4] 刘成立.复杂结构可靠性分析及设计研究[D].西安:西北工业大学,2007.

[5] 易 平.对区间不确定性问题的可靠性度量的探讨[J].计算力学学报,2006,23(2).

[6] 张新锋,赵 彦,施浒立.基于凸集的结构非概率可靠性度量研究[J].Journal ofMechanical Strength,2007,29(4).

[7] 冯世琪,廖林清,贾秋红,等.基于凸集模型的非概率稳健可靠性理论的研究[A].“技术创新与核心能力建设”论文集[C].重庆:重庆汽车工程学会,2006.

[8] 曹鸿钧,段宝岩.基于凸集合模型的非概率可靠性研究[J].计算力学学报,2005,22(5).

[9] 张 峰.结构可靠性的优化算法研究[D].西安:西北工业大学,2007.

[10] 韩宪军,武清玺,杨明珠.蚁群优化算法及其在可靠指标计算中的应用[J].河海大学学报,2007,35(6).

[11] 马 超,吕震宙.隐式极限状态方程的非概率可靠性分析[J].机械强度,2009,31(1).

[12] 吕震宙,冯蕴雯.结构可靠性问题研究的若干进展[J].力学进展,2000,30(1).

2010-03-16)

张盈盈 (1985-),女,河南灵宝人,硕士研究生,主要从事岩土工程结构可靠性研究,Email:0608zhangyingying@163.com。