基于两阶段规划的会议筹备问题研究

阳永生

（长沙民政职业技术学院 文法系，湖南 长沙 410004）

0 引 言

会议筹备的一项重要任务就是为与会代表预订宾馆客房，租借会议室，并租用客车接送代表。然而，由于与会代表数量、对客房的需求及参加分组会议情况等都具有随机性，使得具体的筹备工作变得十分复杂。因此，通过数学建模方法对该问题进行研究具有重要的理论与实践意义。

本文以2009年全国大学生数学建模竞赛D题数据为背景[1]。

1.题分析与模型假设

根据问题的复杂性和实际情况，以经济、方便和代表满意等作为优化目标，从预订宾馆各规格客房、租借会议室、租用客车三个维度进行优化设计，采用两阶段规划方法进行问题的建模与求解。模型具体假设如下：

(1) 满足代表在价位方面的需求是指价位区间而不是具体的价位；

(2) 假设附表 2回执信息中各规格客房需求比例具有代表性；

(3) 两宾馆间的距离不超过 500米时无需派车，道路的宽度按50米计算；

(4) 只在有客房预订的宾馆租借会议室。

2.型建立

2.1.房需求数据预测

为确定各宾馆客房的预订数量，应先确定客房的需求总量及各种规格客房的需求量。设ξ表示本届会议预测与会代表人

由假设(1)及附表2，将合住1~独住3的六类客房依次称为规格1~规格6客房，如果筹备组预订的各规格客房数能满足K位代表的需求，则在置信水平为α的情形下有

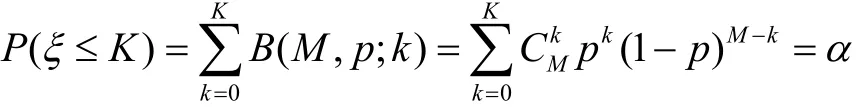
据此，可预测出当置信水平为α时与会代表人数K，由假设(2)，可得到第 j种规格客房的需求量 Nj和客房总量N 。

2.2.型一：客房预订决策模型

客房的预订应使会议筹备组管理方便、代表满意。前者可用所选择的宾馆数尽量少、距离上尽量靠近来衡量；后者则应包含预订客房数不够实际需求的程度、代表是否能得到他要求规格的客房；同时，还应考虑预订客房数超过实际需求时的空房费。

(1) 所选择的宾馆数量为：

如果在宾馆i的预订客房总数大于0，则τi=1，否则τi=0。

(2) 所选择的宾馆在距离上的度量可描述为：

(3) 预订的客房应尽量满足代表在客房规格方面的需求。

设 xij表示在第i个宾馆预订第 j种规格客房的数量；yjk表示需要第k种规格客房而实际安排第 j种规格客房的数量； cjk表示当一个代表需要第k种规格客房而实际安排第j种规格客房时的满意度，具体取值结果如下：

其中，第一部分表示当某规格客房预订数大于需求量时的偏差值，第二部分表示当预订数小于需求量时的偏差值，二者具有互斥性，故增加以下约束[3]

(4) 预订客房的总量过剩或不足导致的“损失”期望值尽量小。

该损失包括预订客房数超过实际需求时造成的一天空房费和预订客房数不够实际需求时引起代表不满的“费用”。

客房数超过实际需求时造成的空房费为

其中， q1表示一间客房一天的空房费。由附表3，根据乐观值准则可得本届会议客房需求总量的最大值 Nmax，采用极值差方法将 f1进行无量纲化处理，得

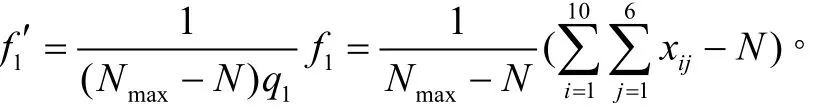
根据假设(2)及附表2，想合住的代表人数占总代表人数的57%，想独住的代表人数占总代表人数的43%，因此，平均每一间客房所代表的人数为1.57人，故预订客房数不够实际需求时引起代表不满的“费用”为

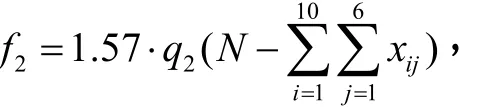
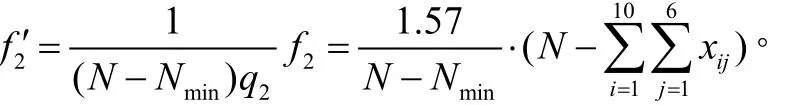
在置信水平为α时，预订客房的总量过剩或不足导致的“损失”的期望值[4,5]为

(5) 目标函数构成。

显然，目标函数(1)~(4)具有不同的指标性质，本文采用极值差方法对其进行无量纲化处理。即

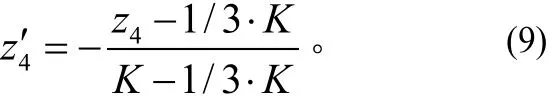
设 aij表示第i个宾馆第 j种规格客房的数量；构造目标

函数(5)~(9)的总目标函数,得客房预订决策模型[6](模型一)如下：

馆中各种规格客房数量的限制；式(11)表示在各宾馆预订的第 j种规格的客房必须全部分配出去；式(12)确保当宾馆i的预订客房总数大于0时 si= 1 ；式(13)表示要求合住的代表不能安排单间；式(16)表示每一种规格客房预订数与相互调配的均衡。

2.3.型二：会议室、客车租赁决策模型

只考虑上午的会议室和客车租赁问题；只在有客房预订的宾馆租借会议室；上午开会前从各宾馆派车，将代表接到各会场，散会后原车返回。会议室、客车租赁决策的主要目标为总费用尽量小。

结合3.2的讨论，可选定在哪些宾馆预订客房，不妨依次对其重新编号为 i=1 ,,n um 。设 Ai表示宾馆i的入住代表人数；示宾馆i中第 j种类型会议室的规模，表示会议室的间数，表示单间会议室半天的租用费；表示第s种型号客车的额定载客量示单位租金；各分组会议所讨论主题的影响因子为(θk>0且∑θk=1)，其含义为第k个分组会议对与会代表的吸引力；示宾馆i第 j种类型会议室是否作为k个分组会会场，为 0-1变量；表示从宾馆l派出的第s种型号客车的数量。

于是，建立会议室、客车租赁决策模型(模型二)如下：

其中，目标函数(17)会议室和客车租赁费用之和；式(18)表示宾馆i第 j种类型会议室的间数限制：式(19)表示每一个主题分组会必须指派 1个会议室；式(20)表示宾馆i第 j种类型会议室的规模限制；式(21)表示保证从宾馆l派出客车的总载客量大于宾馆l需要派车的代表的数量。

3.型求解与结果分析

首先，预测客房需求总量及各规格客房需求量。显然，当置信水平α增加时，客房需求总量预测值会随之增加，其关系如图1所示。

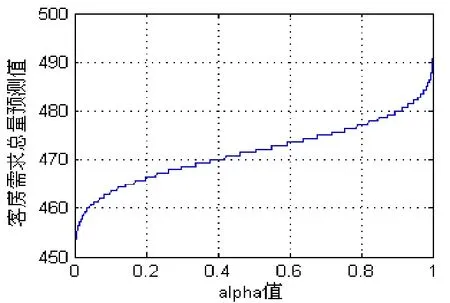
图1.房需求总量与置信水平α关系图

从图1可看出，客房需求总量预测值在473间(0.5α=时)左右波动，且幅度不大。即在50%的概率意义下，客房需求总量小于 473间；而当客房预订量增加约 2.1%时，却可以保证95%的概率意义下不会出现客房不足现象。具体的各规格客房需求量预测值如表1所示。

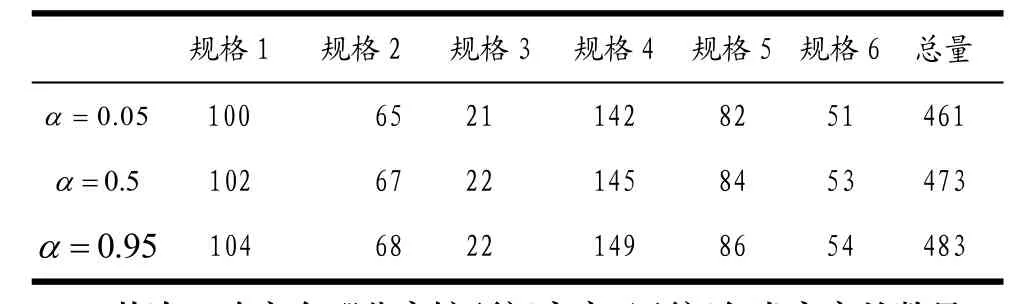
表1.规格客房需求预测值

其次，确定在哪些宾馆预订客房及预订各类客房的数量。根据图1所反映的数据特点，分别以表1中置信水平 α =0.5和 α =0.95时的各规格客房需求数据为基础，权值λi均取为0.2，运用LINGO软件求解[7]模型一，得具体的预订结果如表2所示。从表2可以看出，当α取不同的值时，宾馆的选择及各规格客房之间的调整方向没有变化，但在各规格客房预订数量及调整幅度上有一定差异，同时，各规格客房预订均可以满足85%左右的与会代表在价位方面的需求。

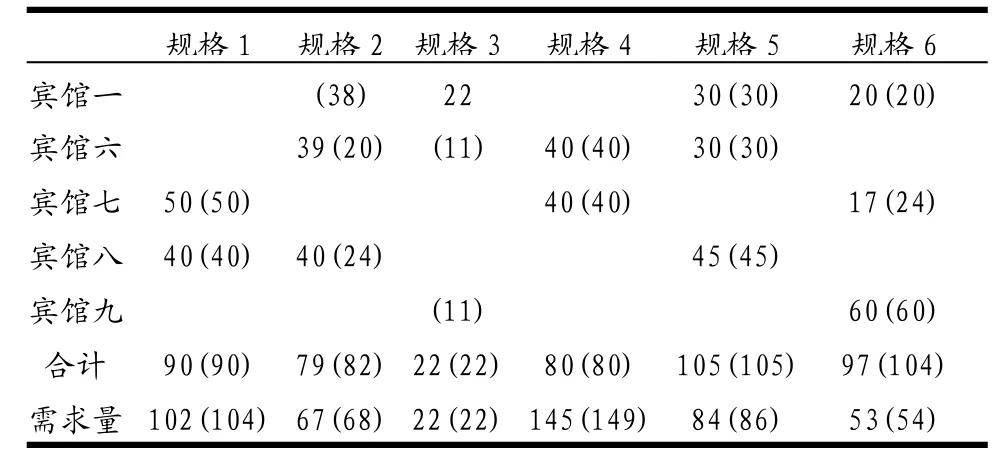
表20.5α=时(0.95α=)具体客房预订情况及对比分析

最后，确定预订会议室及租车的规格和数量。由于没有关于会议主题影响因子的任何信息，不妨假设六个分组会的影响力相等，取θk=1/6，运用LINGO软件求解[4]模型二，得置信水平α=0.5和α=0.95时具体的会议室租借方案均为：租借宾馆七第一、三种类型会议室各1间，宾馆八第一、二种类型会议室各1间，宾馆九第二、三种类型会议室各1间；会议室租借费用为 5600元；无需租车。可见，会议室和客车租赁决策对参数α不敏感，即各宾馆预订客房数量和与会代表总人数发生小范围变化时，对决策结果不会产生影响。

4.语

本文较系统地解决了会议筹备过程中关于与会代表数量预测、宾馆预订、会议室租借和客车租赁决策等问题。首先基于置信水平对与会代表数量进行预测，从而得到各规格客房需求数据；结合问题的实际情况，将会议筹备问题转化为两阶段决策问题，建立相应的数学规划模型，得到了从经济、方便和代表满意等角度考虑的优化方案。其优点在于决策者可以根据各因素的利弊，确定置信水平α，决定具体方案的实施。理论分析与计算结果均表明模型的有效性，与实际生活情形相符。

[1]中国大学生数学建模竞赛[EB/OL].www.mcm. edu. cn, 2009.

[2]刘宝碇,彭锦.不确定理论教程[M].北京:清华大学出版社,2005.

[3]姜启源,谢金星,叶俊.数学模型(第三版)[M],北京:高等教育出版社,2003.

[4]刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社, 2003.

[5]范宏,程浩忠,叶幼君. 基于随机期望值规划的输电网规划方法[J].华东电力,2007,35(12):16~21.

[6]王艳等.出版社的资源配置优化模型[J].工程数学学报,2006,23(7):28~36.

[7]谢金星,刑文训.优化建模与LINDO/LINGO 软件[M],北京:清华大学出版社 ,2007.